Диагональю называется линия, соединяющая два угла выпуклого многоугольника во внутренней его части. У многих типовых плоских фигур диагональ образует внутри многоугольника прямоугольные треугольники, благодаря чему легко вычисляется через теорему Пифагора. В остальных случаях используется теорема косинусов и другие менее простые решения. Более того, диагональ часто становится осью симметрии фигуры, или пересечение двух диагоналей служит центром симметрии, разделяя фигуру на две зеркальные или конгруэнтные части.
Калькуляторы расчета диагонали фигур геометрических фигур
Пожалуйста напишите с чем связна такая низкая оценка:
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»
Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»
Источник: allcalc.ru
Калькуляторы диагоналей
Выполните расчет диагоналей геометрических фигур и объектов при помощи калькулятора диагоналей — рассчитайте диагонали треугольника, прямоугольника, квадрата.
Диагонали в многоугольниках. Есть ли зависимость между количеством вершин и диагоналей в n-угольнике
Все калькуляторы
Калькуляторы диагоналей позволяют рассчитать величину отрезка, соединяющего наиболее дальние несмежные вершины многоугольника. Наши инструменты предназначены для упрощения математических расчетов при выполнении научных и прикладных работ, в т.ч. при организации строительного производства. В качестве теоретического обоснования используются классические геометрические формулы, часть из них приведены ниже.
Формулы диагоналей
- квадрат: d = √2 × a
- прямоугольник: d = √(a 2 + b 2 )
- параллелограмм: d = √(a 2 + b 2 − 2abcos(α))
- трапеция: d = √(h 2 + m 2 )
- куб: d = √3 × a
- параллелепипед: d = √(a 2 + b 2 + c 2 )
- цилиндр: d = √(h 2 + D 2 )
Для того чтобы начать расчет диагоналей, выберите необходимый калькулятор:
Источник: kalk.pro
Многоугольники
причём таких, что два любых отрезка, имеющих общий конец, не лежат на одной прямой (рис.1).
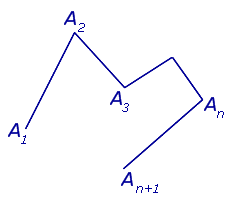
Определение 1 . Ломаной линией с n звеньями называют фигуру L , составленную из отрезков (1), то есть фигуру, заданную равенством
L = [A1 A2] U [A2 A3] U …
… U [An An +1]
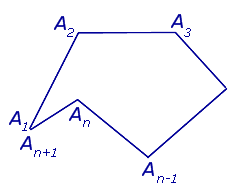
В случае, когда точки A1 и An +1 совпадают, ломаную линию называют замкнутой ломаной линией (рис. 2), в противном случае её называют незамкнутой (рис.1).
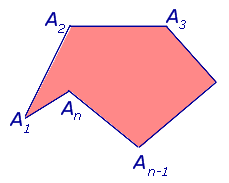
Определение 2 . Многоугольником называют часть плоскости, ограниченную замкнутой ломаной линией без самопересечений (рис. 3). Отрезки, составляющие ломаную линию ( звенья ), называют сторонами многоугольника. Концы отрезков называют вершинами многоугольника.
Площадь квадрата через диагональ Полезный файлик в комментариях)
Определение 3 . Многоугольник называют n – угольником , если он имеет n сторон.
Таким образом, многоугольник, имеющий 3 стороны, называют треугольником , многоугольник, имеющий 4 стороны, называют четырёхугольником и т.д.
Определение 4 . Периметром многоугольника называют сумму длин всех сторон многоугольника.
Величину, равную половине периметра, называют полупериметром .
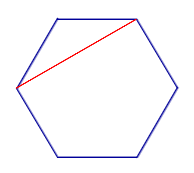
Диагонали n — угольника
Число диагоналей n – угольника равно
| Диагональ многоугольника |
 |
Число диагоналей n – угольника равно
Внешний угол многоугольника
Определение 5 . Два угла называют смежными , если они имеют общую сторону, и их сумма равна 180° (рис.1).

Определение 6 . Внешним углом многоугольника называют угол, смежный с внутренним углом многоугольника (рис.2).
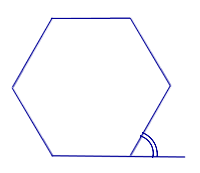
Свойства углов треугольника
Сумма углов треугольника равна 180°
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним
| Углы треугольника |
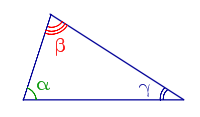 |
Сумма углов треугольника равна 180°


Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним
Свойства углов многоугольника
Сумма углов многоугольника равна
Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360°
| Углы n – угольника |
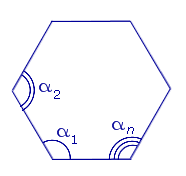 |
Сумма углов многоугольника равна
Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360°
Свойства углов правильного n – угольника
Все углы правильного n – угольника равны
Все внешние углы правильного
n – угольника равны
| Углы правильного n – угольника |
 |
Все углы правильного n – угольника равны
Все внешние углы правильного
n – угольника равны
Доказательства свойств углов многоугольника
Теорема 1 . В любом треугольнике сумма углов равна 180° .
Доказательство . Проведем, например, через вершину B произвольного треугольника ABC прямую DE, параллельную прямой AC, и рассмотрим полученные углы с вершиной в точке B (рис. 3).
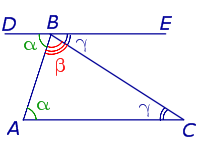
Углы ABD и BAC равны как внутренние накрест лежащие. По той же причине равны углы ACB и CBE . Поскольку углы ABD , ABC и CBE в сумме составляют развёрнутый угол, то и сумма углов треугольника ABC равна 180° . Теорема доказана.
Теорема 2 . Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Доказательство . Проведём через вершину C прямую CE, параллельную прямой AB, и продолжим отрезок AC за точку C (рис.4).
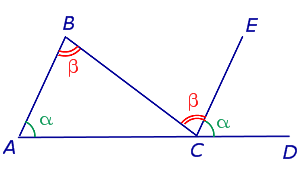
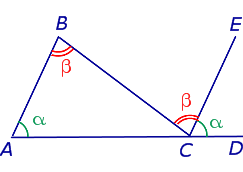
Углы ABC и BCE равны как внутренние накрест лежащие. Углы BAC и ECD равны как соответственные равны как соответственные . Поэтому внешний угол BCD равен сумме углов BAC и ABC . Теорема доказана.
Замечание . Теорема 1 является следствием теоремы 2.
Теорема 3 . Сумма углов n – угольника равна
Доказательство . Выберем внутри n – угольника произвольную точку O и соединим её со всеми вершинами n – угольника (рис. 5).
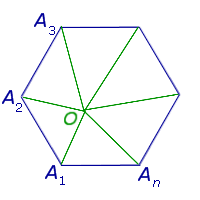
Получим n треугольников:
Сумма углов всех этих треугольников равна сумме всех внутренних углов n – угольника плюс сумма всех углов с вершиной в точке O . Поэтому сумма всех углов n – угольника равна
что и требовалось доказать.
Теорема 4 . Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360° .
Доказательство . Рассмотрим рисунок 6.
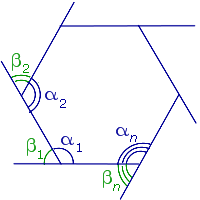
В соответствии рисунком 6 справедливы равенства
Источник: www.resolventa.ru