ОПТИЧЕСКАЯ ОСЬ линзы (вогнутого или выпуклого зеркал а), прямая линия, являющаяся осью симметрии преломляющих поверхностей линзы (отражающей поверхности зеркала); проходит через центры поверхностей перпендикулярно к ним. Оптич. поверхности, обладающие О. о., наз. осесимметричными (см. Зеркало, Линза). О. о. оптической системы — общая ось симметрии всех входящих в систему линз и зеркал.
Смотреть что такое ОПТИЧЕСКАЯ ОСЬ в других словарях:
ОПТИЧЕСКАЯ ОСЬ
линзы (вогнутого или выпуклого зеркала), прямая линия, являющаяся осью симметрии преломляющих поверхностей линзы (отражающей поверхности зеркал. смотреть
ОПТИЧЕСКАЯ ОСЬ
линзы (вогнутого или выпуклого зеркала), прямая линия, являющаяся осью симметрии преломляющих поверхностей линзы (отражающей поверхности зеркал. смотреть
ОПТИЧЕСКАЯ ОСЬ
1) О. о. линзы, вогнутого или выпуклого сферического зеркала — прямая линия, являющаяся осью симметрии преломляющих поверхностей линзы или отражающих п. смотреть
ОПТИЧЕСКАЯ ОСЬ
1) О. о. линзы, вогнутого или выпуклого зеркала — прямая линия, являющаяся осью симметрии преломляющих поверхностей линзы или отражающих поверхностей з. смотреть
ОПТИЧЕСКАЯ ОСЬ
ОПТИЧЕСКАЯ ОСЬ, ..1) кристалла — направление в кристалле, вдоль которого скорость света не зависит от ориентации плоскости поляризации света. Свет, распространяющийся вдоль оптической оси кристалла, не испытывает двойного лучепреломления (см. Кристаллооптика);..2) оптической системы — общая ось вращения поверхностей, составляющих систему; когда такая ось существует, систему называют осесимметрической.
. смотреть
ОПТИЧЕСКАЯ ОСЬ
ОПТИЧЕСКАЯ ось -..1) кристалла — направление в кристалле, вдоль которого скорость света не зависит от ориентации плоскости поляризации света. Свет, распространяющийся вдоль оптической оси кристалла, не испытывает двойного лучепреломления (см. Кристаллооптика);..2) оптической системы — общая ось вращения поверхностей, составляющих систему; когда такая ось существует, систему называют осесимметрической.
. смотреть
ОПТИЧЕСКАЯ ОСЬ
ОПТИЧЕСКАЯ ОСЬ . 1) кристалла — направление в кристалле, вдоль которого скорость света не зависит от ориентации плоскости поляризации света. Свет, распространяющийся вдоль оптической оси кристалла, не испытывает двойного лучепреломления (см. Кристаллооптика);..2) оптической системы — общая ось вращения поверхностей, составляющих систему; когда такая ось существует, систему называют осесимметрической. смотреть
ОПТИЧЕСКАЯ ОСЬ
ОПТИЧЕСКАЯ ОСЬ. 1) кристалла — направление в кристалле, вдоль которого скорость света не зависит от ориентации плоскости поляризации света. Свет, распространяющийся вдоль оптической оси кристалла, не испытывает двойного лучепреломления (см. Кристаллооптика);..2) оптической системы — общая ось вращения поверхностей, составляющих систему; когда такая ось существует, систему называют осесимметрической. смотреть
настройка оптической оси
ОПТИЧЕСКАЯ ОСЬ
— кристалла — направление в кристалле, вдоль которогоскорость света не зависит от ориентации плоскости поляризации света. Свет,распространяющийся вдоль оптической оси кристалла, не испытывает двойноголучепреломления (см. Кристаллооптика);..2) оптической системы — общая осьвращения поверхностей, составляющих систему; когда такая ось существует,систему называют осесимметрической. смотреть
ОПТИЧЕСКАЯ ОСЬ
1) главная О. о. оптической системы — прямая, на которой расположены центры преломляющих или отражающих поверхностей, образующих оптическую систему (линзовую, зеркальную или зеркально линзовую). 2) Побочная О. О. линзы — любая прямая, кроме главной О. О., проходящая через оптический центр тонкой линзы. Астрономический словарь.EdwART.2010. смотреть
ОПТИЧЕСКАЯ ОСЬ
asse ottico; linea f di collimazione
Источник: bse.slovaronline.com
Оптическая ось
Оптическойосьюназывается прямая линия, проходящая через центры кривизны отражающих и преломляющих поверхностей. Если система имеет оптическую ось, то это центрированная оптическая система [2].
Обычно прохождение света через линзу рассматривается в приближении параксиальной оптики, это означает, что направление распространения света всегда составляет малый угол с оптической осью, и лучи пересекают любую поверхность на малом расстоянии от оптической оси.
Линза может быть собирающей или рассеивающей.
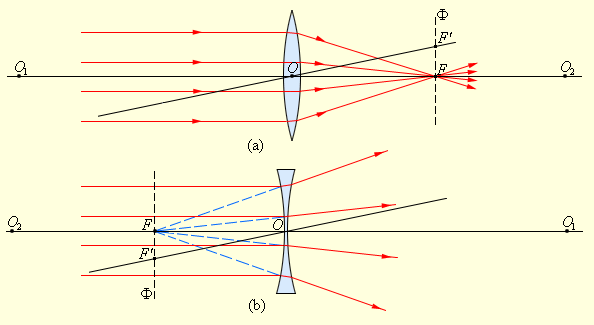
Лучи, параллельные оптической оси, после собирающей линзы проходят через одну и ту же точку. Эта точка называется фокусом линзы. Расстояние от линзы до ее фокуса называется фокусным расстоянием. Плоскость, перпендикулярная оптической оси и проходящая через фокус линзы, называетсяфокальной плоскостью.
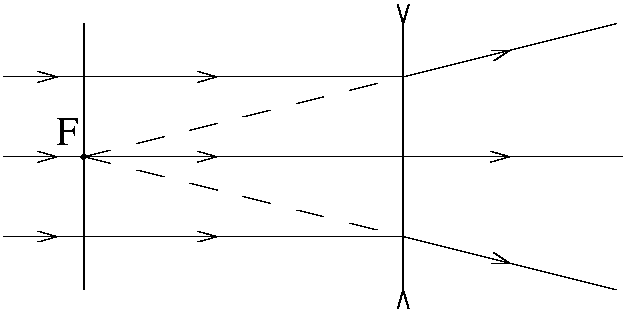
Параллельный пучок лучей, наклоненный к оптической оси, собирается за линзой в одну точку (A на рис. 4) в фокальной плоскости линзы. Рассеивающая линза преобразует параллельный оптической оси пучок лучей в расходящийся пучок (рис. 5). Если расходящиеся лучи продолжить назад, то они пересекутся в одной точке F — фокусе рассеивающей линзы.
При небольшом повороте пучка параллельных лучей точка пересечения перемещается по фокальной плоскости рассеивающей линзы.

Построение изображений
В задачах на построение изображений подразумевается, что протяженный источник света состоит из некогерентных точечных источников. В этом случае изображение протяженного источника света состоит из изображений каждой точки источника, полученных независимо друг от друга.
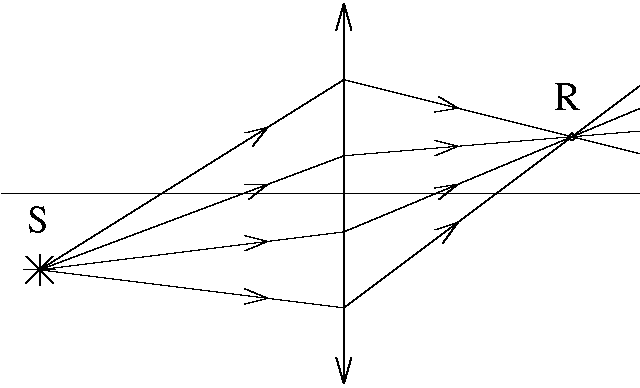
Изображение точечного источника — это точка пересечения всех лучей после прохождения через систему лучей, испущенных точечным источником света. Точечный источник испускает сферическую световую волну. В приближении параксиальной оптики сферическая волна, проходя через линзу (рис. 6), распространяется и далее в виде сферической волны, но с другим значением радиуса кривизны.
Лучи за линзой либо сходятся в одну точку (см. рис.6,а), которую называют действительным изображением источника (точка R), либо расходятся (см. рис. 6,б). В последнем случае продолжения лучей назад пересекаются в некоторой точке I, которая называется мнимым изображением источника света.
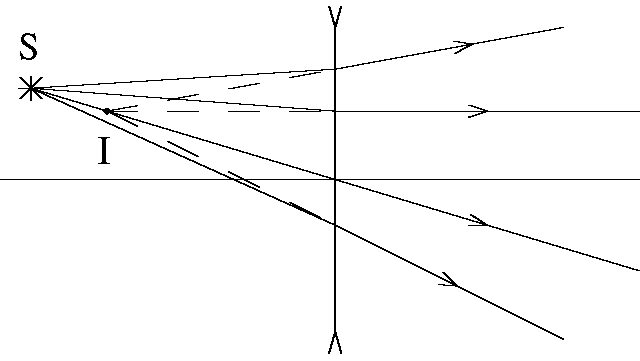
В параксиальном приближении все лучи, исходящие из одной точки до линзы, после линзы пересекаются в одной точке, поэтому для построения изображения точечного источника достаточно найти точку пересечения «удобных нам» двух лучей, эта точка и будет изображением.
Если перпендикулярно оптической оси поставить лист бумаги (экран) так, чтобы изображение точечного источника попало на экран, то в случае действительного изображения на экране будет видна светящаяся точка, а в случае мнимого изображения — нет.
Построение изображения в тонкой линзе
Есть три луча, удобных для построения изображения точечного источника света в тонкой линзе.
Первый луч проходит через центр линзы. После линзы он не изменяет своего направления (рис. 7,а) как для собирающей так и для рассеивающей линзы. Это справедливо только в том случае, если среда с обеих сторон линзы имеет одинаковый показатель преломления. Два других удобных луча рассмотрим на примере собирающей линзы.
Один из них проходит через передний фокус (рис. 7,б), или его продолжение назад проходит через передний фокус (рис. 7,в). После линзы такой луч пойдет параллельно оптической оси. Другой луч проходит до линзы параллельно оптической оси, а после линзы через задний фокус (рис.
7,г).





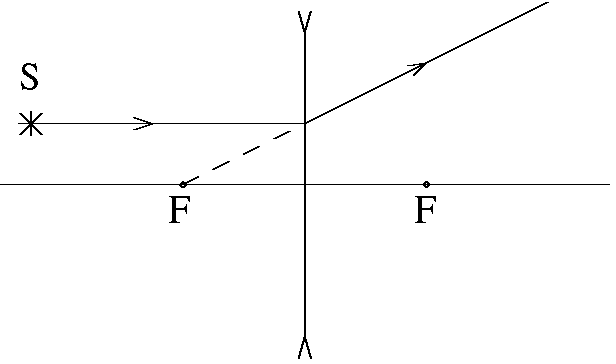
Удобные для построения изображения лучи в случае рассеивающей линзы показаны на рис. 8,а,б.
Точка пересечения, мнимого или действительного, любой пары из этих трех лучей, прошедших линзу, совпадает с изображением источника.
В задачах по оптике иногда возникает потребность найти ход луча не для одного из удобных нам трех лучей, а для произвольного луча (1 на рис. 9,а), направление которого до линзы определено условиями задачи.
В таком случае полезно рассмотреть, например, параллельный ему луч (2 на рис. 9,б), проходящий через центр линзы C, независимо от того, есть или нет такой луч на самом деле.


Параллельные лучи собираются за линзой в фокальной плоскости. Эту точку (A на рис. 9,б) можно найти как точку пересечения фокальной плоскости и вспомогательного луча 2, проходящего линзу без изменения направления. Вторая точка, необходимая и достаточная для построения хода луча 1 после линзы, это точка на тонкой линзе (B на рис. 9,б), в которую упирается луч 1 с той стороны, где его направление известно.
Источник: studfile.net
Тонкие линзы
В тонкой линзе главная оптическая ось пересекается в одной точке – оптическом центре линзы O . Световой луч проходит через оптический центр линзы, не отклоняясь от своего первоначального направления.
Определение 11
Величина D – это оптическая сила линзы, равная обратному фокусному расстоянию.
Диоптрия ( д п т р ) является единицей измерения оптической силы, фокусное расстояние которой равно 1 м : 1 д п т р = м — 1 .
Формула тонкой линзы аналогична формуле сферического зеркала. Можно вывести ее для параксиальных лучей из подобия треугольников на рисунках 3 . 3 . 3 либо 3 . 3 . 4 .
Фокусное расстояние линз записывается с определенными знаками: собирающая линза F > 0 , рассеивающая F < 0 .
Величина d и f тоже подчиняются определенным знакам:
- d > 0 и f > 0 – применительно к действительным предметам (то есть реальным источникам света) и изображений;
- d < 0 и f < 0 – применительно к мнимым источникам и изображениям.
Для случая на рисунке 3 . 3 . 3 F > 0 (линза собирающая), d = 3 F > 0 (действительный предмет).
Из формулы тонкой линзы получаем: f = 3 2 F > 0 , означает, что изображение действительное.
Для случая на рисунке 3 . 3 . 4 F < 0 (линза рассеивающая), d = 2 | F | >0 (действительный предмет), справедлива формула f = — 2 3 F < 0 , следовательно, изображение мнимое.
Линейные размеры изображения зависят от положения предмета по отношению к линзе.
Линейное увеличение линзы Г – это отношение линейных размеров изображения h ‘ и предмета h .
Величину h ‘ удобно записывать со знаками плюс или минус, в зависимости от того, прямое оно или перевернутое. Она всегда положительна. Потому для прямых изображений применяется условие Γ > 0 , для перевернутых Γ < 0 . Из подобия треугольников на рисунках 3 . 3 . 3 и 3 . 3 . 4 нетрудно вывести формулу для расчета линейного увеличения тонкой линзы:
В примере с собирающей линзой на рисунке 3 . 3 . 3 при d = 3 F > 0 , f = 3 2 F > 0 .
В примере с рассеивающей линзой на рисунке 3 . 3 . 4 при d = 2 | F | > 0 , справедлива формула f = — 2 3 F < 0 ; значит, Г = 1 3 >0 – изображение прямое и уменьшенное в три раза.
Оптическая сила D линзы находится в зависимости от радиусов кривизны R 1 и R 2 , ее сферических поверхностей, а также и от показателя преломления n материала линзы. В теории оптики имеет место следующее выражение:
D = 1 F = ( n — 1 ) 1 R 1 + 1 R 2 .
Выпуклая поверхность имеет положительный радиус кривизны, а вогнутая поверхность – отрицательным. Данная формула применима в изготовлении линз с заданной оптической силой.
Многие оптические приборы устроены таким образом, что свет последовательно проходит через 2 или несколько линз. Изображение предмета от 1 -й линзы служит предметом (действительным или мнимым) для 2 -й линзы, выстраивающей, в свою очередь, 2 -е изображение предмета, которое также может быть действительным либо мнимым. Расчет оптической системы из 2 -х тонких линз состоит в
2 -кратном применении формулы линзы, причем расстояние d 2 от 1 -го изображения до 2 -й линзы следует предложить равное величине l – f 1 , где l – это расстояние между линзами.
Астрономическая труба Кеплера и земная труба Галилея
Рассмотрим частный случай – телескопический ход лучей в системе из 2 -х линз, когда и предмет, и 2 -е изображение расположены на бесконечно больших расстояниях друг от друга. Телескопический ход лучей выполняется в зрительных трубах: земной трубе Галилея и астрономической трубе Кеплера.
Тонкая линза имеет некоторые недостатки, которые не позволяют получать изображения высокого разрешения.
Аберрация – это искажение, которое возникает в процессе формирования изображения. В зависимости от расстояния, на котором проводится наблюдение, аберрации могут быть сферическими и хроматическими.
Смысл сферической аберрации в том, что при широких световых пучках лучи, находящиеся на далеком расстоянии от оптической оси, пересекают ее не в месте фокуса. Формула тонкой линзы действует лишь для лучей, которые находятся близко к оптической оси. Изображение удаленного источника, которое создается широким пучком лучей, преломленных линзой, размыто.
Смысл хроматической аберрации в том, что на показатель преломления материала линзы влияет длина световой волны λ . Данное свойство прозрачных сред называют дисперсией. Фокусное расстояние линзы различно для света с различными длинами волн. Данный факт приводит к размытию изображения при излучении немонохроматического света.
Современные оптические приборы оснащены не тонкими линзами, а сложными линзовыми системами, в которых есть возможность исключить некоторые искажения.
В таких приборах, как фотоаппараты, проекторы и т.д., используются собирающие линзы для формирования действительных изображений предметов.
Что представляет собой фотоаппарат
Определение 15
Фотоаппарат – это замкнутая светонепроницаемая камера, в которой изображение запечатленных предметов создается на пленке системой линз – объективом. На время экспозиции объектив открывается и закрывается с помощью специального затвора.
Особенность работы фотоаппарата в том, что на плоской фотопленке получаются довольно резкие изображения предметов, которые находятся на различных расстояниях. Резкость меняется вследствие перемещения объектива относительно фотопленки. Изображения точек, которые не лежат в плоскости резкого наведения, выходят на снимках размытыми в виде рассеянных кружков. Размер d данных кружков можно уменьшить методом диафрагмирования объектива, то есть уменьшения относительного отверстия a F , как показано на рисунке 3 . 3 . 5 . Это в результате увеличивает глубину резкости.
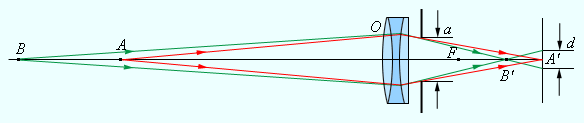
Рисунок 3 . 3 . 5 . Фотоаппарат.
С помощью проекционного аппарата удается снять масштабные изображения. Объектив O проектора фокусирует изображение плоского предмета (диапозитив D ) на удаленном экране Э (рисунок 3 . 3 . 6 ). Система линз K (конденсор) используется для концентрации света источника S на диапозитиве. На экране воссоздается увеличенное перевернутое изображение. Масштаб проекционного устройства можно изменять, приближая или отдаляя экран и одновременно изменяя расстояние между диапозитивом D и объективом O .
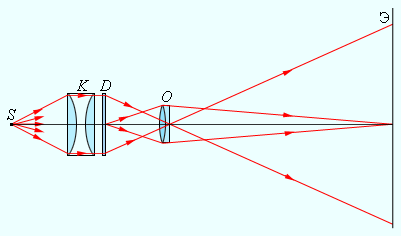
Рисунок 3 . 3 . 6 . Проекционный аппарат.
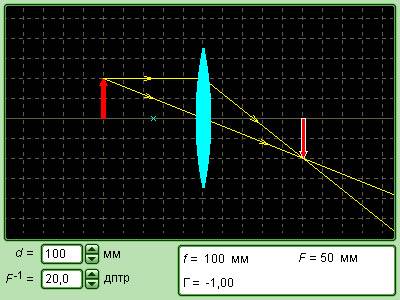
Рисунок 3 . 3 . 7 . Модель тонкой линзы.
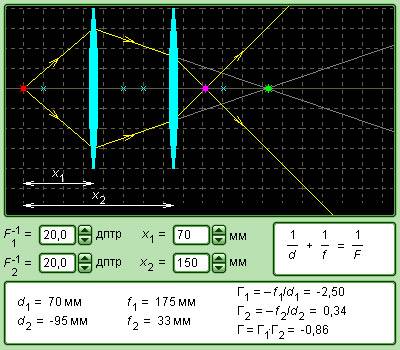
Рисунок 3 . 3 . 8 . Модель системы из двух линз.
Источник: zaochnik-com.com