Для обогрева помещения температура в котором равна тп 25 ТВ 49

Конспект занятия «Задача 10.»

Файл к занятию 20.

Проверка домашнего задания

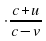
Задание 8. При сближении источника и приёмника звуковых сигналов, движущихся в некоторой среде по прямой навстречу друг другу, частота звукового сигнала, регистрируемого приёмником, не совпадает с частотой исходного сигнала f 0 = 170 Гц и определяется следующим выражением: f = f 0 (Гц), где c — скорость распространения сигнала в среде (в м/с), а u = 13 м/с и v = 8 м/с — скорости приёмника и источника относительно среды соответственно. При какой максимальной скорости c (в м/с) распространения сигнала в среде частота сигнала в приёмнике f будет не менее 175 Гц? Ответ: 722

Задание 10 . В ходе распада радиоактивного изотопа его масса уменьшается по закону

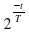
Разбор варианта №3 из сборника ФИПИ/профиль математика 2023

m = m 0 , где m 0 — начальная масса изотопа, t — время, прошедшее от начального момента, T — период полураспада. В начальный момент времени масса изотопа 80 мг. Период его полураспада составляет 2 мин. Найдите, через сколько минут масса изотопа будет равна 5 мг. Ответ: 8

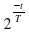
Дополнительно. В ходе распада радиоактивного изотопа его масса уменьшается по закону m = m 0 , где m0 (мг) — начальная масса изотопа, t (мин.) — время, прошедшее от начального момента, T (мин.) — период полураспада. В начальный момент времени масса изотопа m0=200 мг. Период его полураспада T=3 мин. Через сколько минут масса изотопа будет равна 25 мг? Ответ: 9

Решение заданий

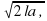
Задание 1. Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением a (в км/ч 2 ). Скорость v (в км/ч) вычисляется по формуле v=где l — пройденный автомобилем путь (в км). Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав 1,1 км, приобрести скорость 110 км/ч. Ответ дайте в км /​ч 2 . Ответ: 5500

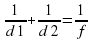
Задание 2. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f =45 см. Расстояние d 1 от линзы до лампочки может изменяться в пределах от 50 до 70 см, а расстояние d 2 от линзы до экрана — в пределах от 160 до 180 см. Изображение на экране будет четким, если выполнено соотношение . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.

Вариант 4 Задание 10 ЕГЭ 2016 Математика, И В Ященко 36 вариантов Решение Ответ

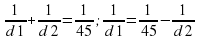
По­сколь­ку f =45 имеем:

Из равенства видно, что наи­мень­ше­му воз­мож­но­му зна­че­нию d 1 со­от­вет­ству­ет наи­боль­шее зна­че­ние левой части по­лу­чен­но­го ра­вен­ства, и, со­от­вет­ствен­но, наи­боль­шее воз­мож­ное зна­че­ние пра­вой части ра­вен­ства. Раз­ность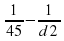

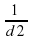в пра­вой части ра­вен­ства до­сти­га­ет наи­боль­ше­го зна­че­ния при неизменном уменьшаемом и наи­мень­шем зна­че­нии вы­чи­та­е­мо­го . Оно до­сти­га­ет­ся при наи­боль­шем воз­мож­ном зна­че­нии зна­ме­на­те­ля d 2. По­это­му d 2=180,

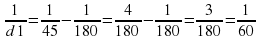
от­ку­да . Значит, d 1=60 см

По усло­вию лам­поч­ка долж­на на­хо­дить­ся на рас­сто­я­нии от 50 до 70 см от линзы. Най­ден­ное зна­че­ние 60 см удо­вле­тво­ря­ет усло­вию. Ответ: 60.

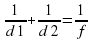
Дополнительно . Для по­лу­че­ния на экра­не уве­ли­чен­но­го изоб­ра­же­ния лам­поч­ки в ла­бо­ра­то­рии ис­поль­зу­ет­ся со­би­ра­ю­щая линза с глав­ным фо­кус­ным рас­сто­я­ни­ем f =50 см. Рас­сто­я­ние d 1 от линзы до лам­поч­ки может из­ме­нять­ся в пре­де­лах от 60 до 80 см, а рас­сто­я­ние d 2 от линзы до экра­на — в пре­де­лах от 150 до 175 см. Изоб­ра­же­ние на экра­не будет чет­ким, если вы­пол­не­но со­от­но­ше­ние. Ука­жи­те, на каком наи­мень­шем рас­сто­я­нии от линзы можно по­ме­стить лам­поч­ку, чтобы еe изоб­ра­же­ние на экра­не было чeтким. Ответ вы­ра­зи­те в сан­ти­мет­рах.

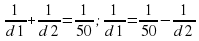
Так как f =50, то имеем:

Из равенства видно, что наи­мень­ше­му воз­мож­но­му зна­че­нию d 1 со­от­вет­ству­ет наи­боль­шее зна­че­ние левой части по­лу­чен­но­го ра­вен­ства, и, со­от­вет­ствен­но, наи­боль­шее воз­мож­ное зна­че­ние пра­вой части ра­вен­ства. Раз­ность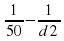

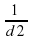в пра­вой части ра­вен­ства до­сти­га­ет наи­боль­ше­го зна­че­ния при неизменном уменьшаемом и наи­мень­шем зна­че­нии вы­чи­та­е­мо­го . Оно до­сти­га­ет­ся при наи­боль­шем воз­мож­ном зна­че­нии зна­ме­на­те­ля d 2. По­это­му d 2=175,

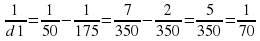
от­ку­да . Значит, d 1=70 см

По усло­вию лам­поч­ка долж­на на­хо­дить­ся на рас­сто­я­нии от 60 до 80 см от линзы. Най­ден­ное зна­че­ние 70 см удо­вле­тво­ря­ет усло­вию. Ответ: 70.

Задание 3. Груз мас­сой 0,25 кг ко­леб­лет­ся на пру­жи­не. Его ско­рость v ме­ня­­ется по за­ко­ну 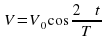где t — время с мо­мен­та на­ча­ла ко­ле­ба­ний, T = 2 с — пе­ри­од ко­ле­ба­ний,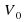

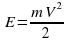=1,6 м/с. Ки­не­ти­че­ская энер­гия E (в джо­у­лях) груза вы­чис­ля­ет­ся по фор­му­ле где m — масса груза в ки­ло­грам­мах, v — ско­рость груза в м/с. Най­ди­те ки­не­ти­че­скую энер­гию груза через 56 се­кунд после на­ча­ла ко­ле­ба­ний. Ответ дайте в джо­у­лях.

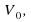
Най­дем ско­рость груза через 56 се­кунд после на­ча­ла ко­ле­ба­ний. Для этого подставим значения t , T в формулу для вычисления скорости:

;

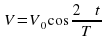
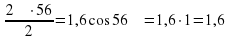
V=1,6cos

Най­дем ки­не­ти­че­скую энер­гию груза через 56 се­кунд после на­ча­ла ко­ле­ба­ний:

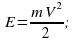E =.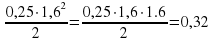

Задание 4. Груз массой 0,8 кг колеблется на пружине. Его скорость v меняется по закону V = V 0 sin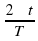

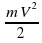, где t ‐ время с момента начала колебаний, T = 16 с – период колебаний, v 0=0,5м/с. Кинетическая энергия Е (в джоулях) груза вычисляется по формуле E =, где m ‐ масса груза в килограммах, V ‐ скорость груза в м/с. Найдите кинетическую энергию груза через 10 секунд после начала колебаний. Ответ дайте в джоулях. (Ответ: 0,05)

Задание 5. Два тела мас­сой m =2 кг каж­дое, дви­жут­ся с оди­на­ко­вой ско­ро­стью V =10 м/с под углом 2

друг к другу. Энер­гия (в джо­у­лях), вы­де­ля­ю­ща­я­ся при их аб­со­лют­но не­упру­гом со­уда­ре­нии опре­де­ля­ет­ся вы­ра­же­ни­ем Q = mV 2 sin 2 . Под каким наи­мень­шим углом 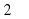(в гра­ду­сах) долж­ны дви­гать­ся тела, чтобы в ре­зуль­та­те со­уда­ре­ния вы­де­ли­лось не менее 100 джо­у­лей?

За­да­ча сво­дит­ся к ре­ше­нию не­ра­вен­ства Q 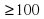Дж на ин­тер­ва­ле 2 (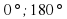) при за­дан­ных зна­че­ни­ях массы тел m =2 кг и их ско­ро­стей V =10 м/с:

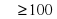
mV 2 sin 2 ;

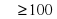
200 sin 2 ;

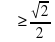
sin 2 ;

Решение данного неравенства

sin 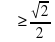то sin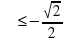

Так как (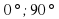) , то sin ,

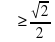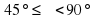
Следовательно, наи­мень­ший угол 2=2

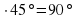
Задание 6 . Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объём и давление связаны соотношением p 1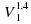

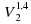​ = p 2 , где p 1 и p 2 — давление газа (в атмосферах) в начальном и конечном состояниях, V 1 и V 2 — объём газа (в литрах) в начальном и конечном состояниях. Изначально объём газа равен 243,2 л, а давление газа равно одной атмосфере. До какого объёма нужно сжать газ, чтобы давление в сосуде стало 128 атмосфер? Ответ дайте в литрах. Ответ: 7,6

Дополнительно. Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объём и давление связаны соотношением p 1 V 1 1,4 ​ = p 2 V 2 1,4 , где p 1 и p 2 — давление газа (в атмосферах) в начальном и конечном состояниях, V 1 и V 2 — объём газа (в литрах) в начальном и конечном состояниях.

Изначально объём газа равен 294,4 л, а давление газа равно одной атмосфере. До какого объёма нужно сжать газ, чтобы давление в сосуде стало 128 атмосфер? Ответ дайте в литрах. Ответ: 9,2

Задание 7. Для опре­де­ле­ния эф­фек­тив­ной тем­пе­ра­ту­ры звёзд ис­поль­зу­ют закон Сте­фа­на-Больц­ма­на, со­глас­но ко­то­ро­му мощ­ность из­лу­че­ния на­гре­то­го тела Р, из­ме­ря­е­мая в ват­тах, прямо про­пор­ци­о­наль­на пло­ща­ди его по­верх­но­сти и четвёртой сте­пе­ни тем­пе­ра­ту­ры: Р=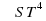

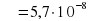, где — по­сто­ян­ная, пло­щадь S из­ме­ря­ет­ся в квад­рат­ных мет­рах, а тем­пе­ра­ту­ра Т — в гра­ду­сах Кель­ви­на. Из­вест­но, что не­ко­то­рая звез­да имеет пло­щадь S= 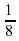1 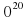м 2 , а из­лу­ча­е­мая ею мощ­ность P=9,234 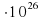Вт. Опре­де­ли­те тем­пе­ра­ту­ру этой звез­ды. При­ве­ди­те ответ в гра­ду­сах Кель­ви­на. Ответ: 6000.

Задание 8. Во­до­лаз­ный ко­ло­кол, со­дер­жа­щий υ = 2 моля воз­ду­ха при дав­ле­нии p1 = 1,75 ат­мо­сфе­ры, мед­лен­но опус­ка­ют на дно водоёма. При этом про­ис­хо­дит изо­тер­ми­че­ское сжа­тие воз­ду­ха до ко­неч­но­го дав­ле­ния p2. Ра­бо­та, со­вер­ша­е­мая водой при сжа­тии воз­ду­ха, опре­де­ля­ет­ся вы­ра­же­ни­ем A = , где — по­сто­ян­ная, T = 300 K — тем­пе­ра­ту­ра воз­ду­ха. Най­ди­те, какое дав­ле­ние p2 (в атм) будет иметь воз­дух в ко­ло­ко­ле, если при сжа­тии воз­ду­ха была со­вер­ше­на ра­бо­та в 15 960 Дж. Ответ: 7.

Задание 9. Во­до­лаз­ный ко­ло­кол, со­дер­жа­щий в на­чаль­ный мо­мент вре­ме­ни υ=4 моля воз­ду­ха объeмом V 1=14 л, мед­лен­но опус­ка­ют на дно водоeма. При этом про­ис­хо­дит изо­тер­ми­че­ское сжа­тие воз­ду­ха до ко­неч­но­го объeма V 2. Ра­бо­та, со­вер­ша­е­мая водой при сжа­тии воз­ду­ха, опре­де­ля­ет­ся вы­ра­же­ни­ем A= (Дж), где по­сто­ян­ная, а T =300 К — тем­пе­ра­ту­ра воз­ду­ха. Какой объeм V 2 (в лит­рах) ста­нет за­ни­мать воз­дух, если при сжа­тии газа была со­вер­ше­на ра­бо­та в 27 840 Дж?

Задание 10. Для обо­гре­ва по­ме­ще­ния, тем­пе­ра­ту­ра в ко­то­ром равна Tп​=20 °​C , через ра­ди­а­тор отоп­ле­ния, про­пус­ка­ют го­ря­чую воду тем­пе­ра­ту­рой Tв​=60 °​C . Рас­ход про­хо­дя­щей через трубу воды m=0,3 кг /​ с. Про­хо­дя по трубе рас­сто­я­ние x (м), вода охла­жда­ет­ся до тем­пе­ра­ту­ры T , причeм x=α⋅⋅log2​ (м), где с=4200 – теплоeмкость воды, – ко­эф­фи­ци­ент теп­ло­об­ме­на, а α =0,7 – по­сто­ян­ная. До какой тем­пе­ра­ту­ры (в гра­ду­сах Цель­сия) охла­дит­ся вода, если длина трубы 84 м? Ответ: 30

Задание 11. Ёмкость высоковольтного конденсатора в телевизоре C=3⋅10 − 6 Ф. Параллельно с конденсатором подключён резистор с сопротивлением R=2⋅10 6 Ом. Во время работы телевизора напряжение на конденсаторе U0=30 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением t=αRClog2 (с), где α =1,4 — постоянная.

Определите наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 25,2 секунды. Ответ дайте в кВ (киловольтах). Ответ: 3,75

Задание 12. В розетку электросети подключена электрическая духовка, сопротивление которой составляет R1 =72 Ом. Параллельно с ней в розетку предполагается подключить электрообогреватель, сопротивление которого R2 (в Ом).
При параллельном соединении двух электроприборов с сопротивлениями R1 и R2 их общее сопротивление вычисляется по формуле Rобщ = Для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 8 Ом. Определите наименьшее возможное сопротивление электрообогревателя. Ответ дайте в омах. Ответ:9

Дополнительно. Ёмкость высоковольтного конденсатора в телевизоре C=6⋅10− 6 Ф. Параллельно с конденсатором подключён резистор с сопротивлением R=8⋅10 6 Ом. Во время работы телевизора напряжение на конденсаторе U0=34 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением t=αRClog2 (с), где α=0,8 — постоянная.

Определите наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 76,8 секунды. Ответ дайте в кВ (киловольтах).

Задание 13. Рей­тинг R ин­тер­нет-ма­га­зи­на вы­чис­ля­ет­ся по фор­му­ле R = r пок — ,

где m =, — сред­няя оцен­ка ма­га­зи­на по­ку­па­те­ля­ми (от 0 до 1), — оцен­ка ма­га­зи­на экс­пер­та­ми (от 0 до 0,7) и К — число по­ку­па­те­лей, оце­нив­ших ма­га­зин. Най­ди­те рей­тинг ин­тер­нет-ма­га­зи­на «Альфа», если число по­ку­па­те­лей, оста­вив­ших отзыв о ма­га­зи­не, равно 26, их сред­няя оцен­ка равна 0,68,а оцен­ка экс­пер­тов равна 0,23.Ответ:0,63.

Задание 14. Не­за­ви­си­мое агент­ство на­ме­ре­но вве­сти рей­тинг R но­вост­ных из­да­ний на ос­но­ве по­ка­за­те­лей ин­фор­ма­тив­но­сти In , опе­ра­тив­но­сти Op и объ­ек­тив­но­сти Tr пуб­ли­ка­ций. Каж­дый по­ка­за­тель оце­ни­ва­ет­ся це­лы­ми чис­ла­ми от -2 до 2.

Ана­ли­тик, со­став­ля­ю­щий фор­му­лу, счи­та­ет, что объ­ек­тив­ность пуб­ли­ка­ций це­нит­ся вдвое, а ин­фор­ма­тив­ность — втрое до­ро­же, чем опе­ра­тив­ность. В ре­зуль­та­те, фор­му­ла при­мет вид

R = . Каким долж­но быть число A , чтобы из­да­ние, у ко­то­ро­го все по­ка­за­те­ли наи­боль­шие, по­лу­чи­ло рей­тинг 30? Ответ:0,4.

Введём систему координат:
ось Oy направим вертикально вверх вдоль одного из пилонов, а ось Ox направим вдоль полотна моста, как показано
на рисунке. В этой системе координат линия, по которой провисает цепь моста, задаётся формулой

y=0,0029x 2 ​−0,53x+28,

где x и y измеряются в метрах. Найдите длину ванты, расположенной
в 90 метрах от пилона. Ответ дайте в метрах. Ответ: 3,79

Задания по теме для самостоятельного решения

Задание 1

Ав­то­мо­биль раз­го­ня­ет­ся на пря­мо­ли­ней­ном участ­ке шоссе с по­сто­ян­ным уско­ре­ни­ем a км/ч 2 . Ско­рость вы­чис­ля­ет­ся по фор­му­ле v= 2 l a , где l — прой­ден­ный ав­то­мо­би­лем путь. Най­ди­те уско­ре­ние, с ко­то­рым дол­жен дви­гать­ся ав­то­мо­биль, чтобы, про­ехав 0,25 километра, при­об­ре­сти ско­рость 60 км/ч. Ответ вы­ра­зи­те в км/ч 2

Задание 2

Для опре­де­ле­ния эф­фек­тив­ной тем­пе­ра­ту­ры звёзд ис­поль­зу­ют закон Сте­фа­на-Больц­ма­на, со­глас­но ко­то­ро­му мощ­ность из­лу­че­ния на­гре­то­го тела Р, из­ме­ря­е­мая в ват­тах, прямо про­пор­ци­о­наль­на пло­ща­ди его по­верх­но­сти и четвёртой сте­пе­ни тем­пе­ра­ту­ры: Р= σ S T 4 , где σ = 5 , 7 * 10 — 8 м 2 — по­сто­ян­ная, пло­щадь S из­ме­ря­ет­ся в квад­рат­ных мет­рах, а тем­пе­ра­ту­ра Т — в гра­ду­сах Кель­ви­на. Из­вест­но, что не­ко­то­рая звез­да имеет пло­щадь S= 1 81 10 21 м 2 , а из­лу­ча­е­мая ею мощ­ность P= 9 ,1 2 * 10 26 Вт. Опре­де­ли­те тем­пе­ра­ту­ру этой звез­ды. При­ве­ди­те ответ в гра­ду­сах Кель­ви­на.

Задание 3

. Водолазный колокол, содержащий υ=5 моль воздуха при давлении p1 =2,3 атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления p2. Работа, совершаемая водой при сжатии воздуха, определяется выражением A= a v T log 2 p 1 p 2 , где a = 15 , 6 Д ж м о л ь * К — постоянная, T=300 K — температура воздуха. Найдите, какое давление p2 (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 23 400 Дж.

Источник: urokidoma.org

Для обогрева помещения температура в котором равна тп 25 тв 49

Опубликовано 29.09.2017 по предмету Математика от Гость >> Оцени ответ

Не нашёл ответ?

Если тебя не устраивает ответ или его нет, то попробуй воспользоваться поиском на сайте и найти похожие ответы по предмету Математика.

Самые новые вопросы

Гадать еще раз

• Алгебра
• Математика
• Русский язык
• Українська мова
• Информатика
• Геометрия
• Химия
• Физика
• Экономика
• Право
• Английский язык
• География
• Биология
• Другие предметы
• Обществознание
• История
• Литература
• Українська література
• Беларуская мова
• Қазақ тiлi

Показать ещё

Источник: nebotan.com