27992. Уравнение процесса, в котором участвовал газ, записывается в виде pV a = const, где p (Па) — давление в газе, V — объем газа в кубических метрах, a – положительная константа. При каком наименьшем значении константы a уменьшение вдвое раз объема газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 4 раза.
Выразим из заданной формулы давление:
Необходимо найти наименьшее a, при котором, уменьшение объёма газа вдвое, приводит к увеличению давления в 4 или более раз, значит:
Основание степени меньше единицы, поэтому знак меняется на противоположный:
При наименьшем значении a равном 2 выполнится поставленное условие.
Решение №1582 Уравнение процесса, в котором участвовал газ, записывается в виде P·Va = const …
Уравнение процесса, в котором участвовал газ, записывается в виде P·V a = const, где P (Па) – давление в газе, V – объем газа в кубических метрах, a – положительная константа. При каком наименьшем значении константы a уменьшение объёма газа в 16 раз приводит к увеличению давления не менее, чем в 32 раза?
Все Задания 9 ЕГЭ 2024 ПРОФИЛЬ из Банка ФИПИ (Математика Школа Пифагора)
Источник задания: alexlarin.net
уменьшение объёма газа в 16 раз приводит к увеличению давления не менее, чем в 32 раза
16 a = 32
2 4a = 2 5
4a = 5
Ответ: 1,25.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 2.8 / 5. Количество оценок: 8
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.
Решение задачи 10. Вариант 217
Уравнение процесса, в котором участвовал газ, записывается в виде
pV^a=const, где p (Па) – давление в газе, – объeм газа в кубических метрах,
a – положительная константа. При каком наименьшем значении константы a
уменьшение вдвое раз объeма газа, участвующего в этом процессе, приводит к
увеличению давления не менее, чем в 4 раза?
Для физиков это задача решается на легке)
( pV^a≥ 4p*frac ) сократим на p и V^a, и умножим на 2^a
Уравнение процесса в котором участвовал газ записывается в виде pv const при каком наименьшем 25
Прототип задания 11 (№ 27992)
Уравнение процесса, в котором участвовал газ, записывается в виде (pV^a = const), где p (Па) — давление в газе, V — объeм газа в кубических метрах, a — положительная константа. При каком наименьшем значении константы a уменьшение вдвое раз объeма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 4 раза?
$$4p cdot left(frac right)^a = pV^a,$$
Наименьшее значение константы а равно 2.
Прототип задания 11 (№ 27993)
Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объём и давление связаны соотношением (p_1V_1^ = p_2V_2^ ), где (p_1) и (p_2) — давление газа (в атмосферах) в начальном и конечном состояниях, (V_1) и (V_2) — объём газа (в литрах) в начальном и конечном состояниях. Изначально объём газа равен 1,6 л, а давление газа равно одной атмосфере. До какого объёма нужно сжать газ, чтобы давление в сосуде стало 128 атмосфер? Ответ дайте в литрах.
Вариант 4 Задание 2 ЕГЭ 2016 Математика, И В Ященко 36 вариантов Решение Ответ
$$1 cdot 1,6^ = 128 cdot V_2^ , $$
$$1,6 = 2^5 cdot V_2,$$
Газ нужно сжать до объема 0,05 литров.
Прототип задания 11 (№ 27994)
В телевизоре ёмкость высоковольтного конденсатора в телевизоре (C = 2 cdot 10^ ) Ф. Параллельно с конденсатором подключён резистор с сопротивлением (R = 5 cdot 10^6) Ом. Во время работы телевизора напряжение на конденсаторе (U_0 = 16) кВ. После выключения телевизора напряжение на конденсаторе убывает до значения (U) (кВ) за время, определяемое выражением (t=alpha RClog _ frac > ) (с), где (alpha =0,7) — постоянная. Определите напряжение на конденсаторе, если после выключения телевизора прошло 21 с. Ответ дайте в киловольтах.
$$0,7 cdot 5 cdot 10^6 cdot 2 cdot 10^ log _ frac = 21, $$
Напряжение на конденсаторе через 21 с после выключения телевизора равно 2 кВ.
Прототип задания 11 (№ 27995)
Для обогрева помещения, температура в котором поддерживается на уровне (T_ > = 20^circ >), через радиатор отопления пропускают горячую воду. Расход проходящей через трубу радиатора воды m = 0,3 кг/с. Проходя по трубе расстояние x, вода охлаждается от начальной температуры (T_ > = 60^circ >) до температуры T, причём (x = alpha frac > log _2 frac > — T_ > >> > >>), где (c = 4200frac cdottext > > cdot ^circ >>>) — теплоёмкость воды, (gamma = 21frac >>> > cdot ^circ >>>) — коэффициент теплообмена, а (alpha=0,7) — постоянная. Найдите, до какой температуры (в градусах Цельсия) охладится вода, если длина трубы радиатора равна 84 м.
Источник: all-equa.ru
МАТЕМАТИКАГИАИЕГЭ / Все ПРОТОТИПЫ ЕГЭ Ларин!
35. Прототип задания 11 (№ 27987) Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной l км с постоянным ускорением a км/ч 2 , вычисляется по формуле v 2 2 la . Определите, с какой наименьшей скоростью будет двигаться автомобиль на расстоянии 1 километра от старта, если по конструктивным особенностям автомобиля приобретаемое им ускорение не меньше 5000 км/ч 2 . Ответ выразите в км/ч. 36.
Прототип задания 11 (№ 27988) Для поддержания навеса планируется использовать цилиндрическую колонну. Давление P (в паскалях), оказываемое навесом и колонной на опору, определяется по формуле P 4 π mg D 2 , где m = 1200 кг − общая масса навеса и колонны, D − диаметр колонны (в метрах).
Считая ускорение свободного падения g = 10 м/с 2 , а π = 3, определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 400000 Па. Ответ выразите в метрах. 37.
Прототип задания 11 (№ 27989) Автомобиль, масса которого равна m = 2160 кг, начинает двигаться с ускорением, которое в течение t секунд остается неизменным, и проходит за это время путь S = 500 метров. Значение силы (в ньютонах), приложенной в это время к автомобилю, равно F 2 t mS 2 . Определите наибольшее время после начала движения автомобиля, за которое он пройдет указанный путь, если известно, что сила F , приложенная к автомобилю, не меньше 2400 Н. Ответ выразите в секундах.
38. Прототип задания 11 (№ 27990) При адиабатическом процессе для идеального газа выполняется закон pV k const , где p − давление в газе в паскалях, V − объем газа в кубических метрах. В ходе эксперимента с одноатомным идеальным газом (для него k = 5/3) из начального состояния, в котором const 10 5 Па ∙ м 5 , газ начинают сжимать.
Какой наибольший объем V может занимать газ при давлениях p не ниже 3,2 ∙ 10 6 Па? Ответ выразите в кубических метрах. 39. Прототип задания 11 (№ 27991) В ходе распада радиоактивного изотопа его масса уменьшается по закону m t m 2 t , где m (мг) 0 T 0 − начальная масса изотопа, t (мин.) − время, прошедшее от начального момента, T (мин.) − период полураспада.
В начальный момент времени масса изотопа m 0 = 40 мг. Период его полураспада T = 10 мин. Через сколько минут масса изотопа будет равна 5 мг? 40. Прототип задания 11 (№ 27992) Уравнение процесса, в котором участвовал газ, записывается в виде pV а const , где p (Па) − давление в газе, V − объем газа в кубических метрах, a – положительная константа.
При каком наименьшем значении константы a уменьшение вдвое раз объема газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 4 раза? 41. Прототип задания 11 (№ 27993) Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ.
При этом объем и давление связаны соотношением pV 1,4 const , где p (атм.) − давление в газе, V − объем газа в литрах. Изначально объем газа равен 1,6 л, а его давление равно одной атмосфере. В соответствии с техническими характеристиками поршень насоса выдерживает давление не более 128 атмосфер. Определите, до какого минимального объема можно сжать газ. Ответ выразите в литрах.
42. Прототип задания 11 (№ 27994) Eмкость высоковольтного конденсатора в телевизоре С 2 10 6 Ф. Параллельно с конденсатором подключeн резистор с сопротивлением R 5 10 6 Ом. Во время работы телевизора напряжение на конденсаторе U 0 16 кВ. После выключения телевизора напряжение на конденсаторе убывает до 6
| значения U (кВ) за время, определяемое выражением t αRC log | 2 | U 0 | (с), где α = 0,7 − постоянная. |
| U |
Определите наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 21 с. Ответ дайте в кВ (киловольтах). 43. Прототип задания 11 (№ 27995) Для обогрева помещения, температура в котором равна T П 20 С , через радиатор отопления, пропускают горячую воду температурой T В 60 С . Расход проходящей через трубу воды m = 0,3 кг/с.
| Проходя по | трубе расстояние | x (м), вода охлаждается | до температуры T ( C), | ||||||
| причем x α cm log | T B T П | (м), где с 4200 | Дж | – теплоемкость воды, | γ 21 | В т | – коэффициент | ||
| кг С | м С | ||||||||
| γ | 2 T T | ||||||||
| П | |||||||||
теплообмена, а α = 0,7 − постоянная. До какой температуры (в градусах Цельсия) охладится вода, если длина трубы 84 м? 44. Прототип задания 11 (№ 27996) Водолазный колокол, содержащий в начальный момент времени υ 3 моля воздуха объемом V 1 = 8л, медленно опускают на дно водоема. При этом происходит изотермическое сжатие воздуха до конечного
| V 1 | |
| объeма V 2 . Работа, совершаемая водой при сжатии воздуха, определяется выражением A αυ T log 2 V | |
| 2 | |
| (Дж), где α 5,75 постоянная, а T 300 К − температура воздуха. Какой объем V 2 | (в литрах) станет |
| занимать воздух, если при сжатии газа была совершена работа в 10350 Дж? | |
| 45. Прототип задания 11 (№ 27997) | |
| Находящийся в воде водолазный колокол, содержащий υ 2 моля воздуха при | давлении p 1 1,5 |
атмосферы, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха.
| Работа, | совершаемая водой при сжатии воздуха, определяется выражением A αυ T log | 2 | p 2 | (Дж), где | |
| p | |||||
| 1 | |||||
| α 5,75 | − постоянная, T 300 К − температура воздуха, p 1 (атм.) − начальное давление, | а p 2 (атм.) − | |||
конечное давление воздуха в колоколе. До какого наибольшего давления p 2 можно сжать воздух в колоколе, если при сжатии воздуха совершается работа не более чем 6900 Дж? Ответ приведите в атмосферах. 46. Прототип задания 11 (№ 27998)
| Мяч бросили под углом | α к | плоской | горизонтальной поверхности земли. Время полета мяча | ||
| (в секундах) определяется | по | формуле | t | 2 v 0 sinα | . При каком наименьшем значении угла α |
| g | |||||
(в градусах) время полета будет не меньше 3 секунд, если мяч бросают с начальной скоростью v 0 30 м/с? Считайте, что ускорение свободного падения g = 10 м/с 2 . 47. Прототип задания 11 (№ 27999) Деталью некоторого прибора является квадратная рамка с намотанным на неe проводом, через который пропущен постоянный ток. Рамка помещена в однородное магнитное поле так, что она может вращаться. Момент силы Ампера, стремящейся повернуть рамку, (в Н ∙ м) определяется формулой
| M NIBl 2 sinα , где | I 2 A − сила тока | в рамке, B 3 10 3 Тл − значение индукции магнитного поля, |
| l 0,5м − размер | рамки, N 1000 – | число витков провода в рамке, α − острый угол между |
перпендикуляром к рамке и вектором индукции. При каком наименьшем значении угла α (в градусах) рамка может начать вращаться, если для этого нужно, чтобы раскручивающий момент M был не меньше 0,75 Н ∙ м? 48. Прототип задания 11 (№ 28000) Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону U U 0 sin ω t φ , где t −
| время в секундах, амплитуда U 0 2 В, частота | ω 120/ с , фаза | 30. Датчик настроен так, что |
| 7 |
если напряжение в нeм не ниже чем 1 В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть? 49. Прототип задания 11 (№ 28002) Очень лeгкий заряженный металлический шарик зарядом q 210 6 Кл скатывается по гладкой наклонной плоскости.
В момент, когда его скорость составляет v = 5 м/с, на него начинает действовать постоянное магнитное поле, вектор индукции B которого лежит в той же плоскости и составляет угол α с направлением движения шарика. Значение индукции поля B 410 3 Тл. При этом на шарик действует сила Лоренца, равная F л qvB sin α (Н) и направленная вверх перпендикулярно плоскости.
При каком наименьшем значении угла 
[0°; 180°] шарик оторвется от поверхности, если для этого нужно, чтобы сила F л была не менее, чем 210 8 Н? Ответ дайте в градусах. 50. Прототип задания 11 (№ 28003) Небольшой мячик бросают под острым углом α к плоской горизонтальной поверхности земли.
Максимальная высота полета мячика, выраженная в метрах, определяется формулой H 4 v o g 2 1 — cos 2 α , где v 0 20 м/с − начальная скорость мячика, а g − ускорение свободного падения (считайте g = 10 м/с 2 ). При каком наименьшем значении угла α (в градусах) мячик пролетит над стеной высотой 4 м на расстоянии 1 м? 51. Прототип задания 11 (№ 28004) Небольшой мячик бросают под острым углом α к плоской горизонтальной поверхности земли. v 2 Расстояние, которое пролетает мячик, вычисляется по формуле L g o sin2α (м), где v 0 20 м/с − начальная скорость мячика, а g − ускорение свободного падения (считайте g = 10 м/с 2 ). При каком наименьшем значении угла (в градусах) мячик перелетит реку шириной 20 м? 52.
Прототип задания 11 (№ 28005) Плоский замкнутый контур площадью S = 0,5 м находится в магнитном поле, индукция которого равномерно возрастает. При этом согласно закону электромагнитной индукции Фарадея в контуре появляется ЭДС индукции, значение которой, выраженное в вольтах, определяется формулой 
, где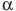 
− острый угол между направлением магнитного поля и перпендикуляром к контуру, a 410 4 Тл/с − постоянная, S − площадь замкнутого контура, находящегося в магнитном поле (в м 
При каком минимальном угле α (в градусах) ЭДС индукции не будет превышать 10 -4 В? 53. Прототип задания 11 (№ 28006) Трактор тащит сани с силой F = 80 кН, направленной под острым углом α к горизонту. Работа трактора (в килоджоулях) на участке длиной S = 50м вычисляется по формуле A = FS cos α . При каком максимальном угле α (в градусах) совершeнная работа будет не менее 2000 кДж? 54.
Прототип задания 11 (№ 28007) Трактор тащит сани с силой F = 50 кН, направленной под острым углом α к горизонту. Мощность (в киловаттах) трактора при скорости v = 3 м/с равна N = Fv cos . При каком максимальном угле α (в градусах) эта мощность будет не менее 75 кВт? 55.
Прототип задания 11 (№ 28008) При нормальном падении света с длиной волны λ = 400 нм на дифракционную решетку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол φ (отсчитываемый от перпендикуляра к решетке), под которым наблюдается максимум, и номер максимума k связаны соотношением d sin φ = k λ . Под каким минимальным углом φ (в градусах) можно наблюдать второй максимум на решетке с периодом, не превосходящим 1600 нм? 56. Прототип задания 11 (№ 28009) Два тела массой m = 2 кг каждое, движутся с одинаковой скоростью v = 10 м/с под углом 2 α друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении определяется 8
выражением Q mv 2 sin 2 α . Под каким наименьшим углом 2 α (в градусах) должны двигаться тела, чтобы в результате соударения выделилось не менее 50 джоулей? 57. Прототип задания 11 (№ 28010) Катер должен пересечь реку шириной L = 100 м и со скоростью течения u = 0,5 м/с так, чтобы причалить точно напротив места отправления. Он может двигаться с разными скоростями, при этом время в пути, измеряемое в секундах, определяется выражением t u L ctgα , где α − острый угол, задающий направление его движения (отсчитывается от берега). Под каким минимальным углом α (в градусах) нужно плыть, чтобы время в пути было не больше 200 с? 58. Прототип задания 11 (№ 28011) Скейтбордист прыгает на стоящую на рельсах платформу, со скоростью v = 3 м/с под острым углом α к
| m | ||||
| рельсам. От толчка платформа начинает ехать со скоростью | u | v cos α | (м/с), где m | = 80 кг − |
| m M | ||||
масса скейтбордиста со скейтом, а M = 400 кг − масса платформы. Под каким максимальным углом α (в градусах) нужно прыгать, чтобы разогнать платформу не менее чем до 0,25 м/с? 59. Прототип задания 11 (№ 28012) Груз массой 0,08 кг колеблется на пружине со скоростью, меняющейся по закону v t 0,5sin πt , где t − время в секундах.
Кинетическая энергия груза, измеряемая в джоулях, вычисляется по формуле E mv 2 2 , где m − масса груза (в кг), v − скорость груза (в м/с). Определите, какую долю времени из первой секунды после начала движения кинетическая энергия груза будет не менее 5 10 3 Дж. Ответ выразите десятичной дробью, если нужно, округлите до сотых. 60.
Прототип задания 11 (№ 28013) Груз массой 0,08 кг колеблется на пружине со скоростью, меняющейся по закону v t 0,5cos πt , где t − время в секундах. Кинетическая энергия груза вычисляется по формуле E mv 2 2 , где m − масса груза (в кг), v − скорость груза (в м/с). Определите, какую долю времени из первой секунды после начала движения кинетическая энергия груза будет не менее 5 10 3 Дж.
Ответ выразите десятичной дробью, если нужно, округлите до сотых. 61. Прототип задания 11 (№ 28014) Скорость колеблющегося на пружине груза меняется по закону v t 5sin πt (см/с), где t − время в секундах. Какую долю времени из первой секунды скорость движения превышала 2,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
62. Прототип задания 11 (№ 263802) Расстояние от наблюдателя, находящегося на небольшой высоте h километров над землeй до наблюдаемой им линии горизонта вычисляется по формуле l 
2 Rh , где R = 6400 (км) − радиус Земли. С какой высоты горизонт виден на расстоянии 4 километра? Ответ выразите в километрах. 63.
Прототип задания 11 (№ 317096) Независимое агентство намерено ввести рейтинг R новостных изданий на основе показателей информативности In , оперативности Op и объективности Tr публикаций. Каждый показатель оценивается целыми числами от − 2 до 2. Аналитик, составляющий формулу, считает, что информативность публикаций ценится втрое, а объективность – вдвое дороже, чем оперативность. В результате, формула примет вид R 3 In Op 2 Tr . A Каким должно быть число A , чтобы издание, у которого все показатели наибольшие, получило рейтинг 30? 9
64. Прототип задания 11 (№ 317097) Рейтинг R интернет-магазина вычисляется по формуле
| R r | r пок r экс | , | ||
| пок | К 1 | 0,02 К | ||
| r пок 0,1 | ||||
где r пок − средняя оценка магазина покупателями (от 0 до 1), r экс − оценка магазина экспертами (от 0 до 0,7) и K − число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина «Альфа», если число покупателей, оставивших отзыв о магазине, равно 10, их средняя оценка равна 0,9, а оценка экспертов равна 0,35. 65.
Прототип задания 11 (№ 319859) Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности In , оперативности Op , объективности публикаций Tr , а также качества сайта Q . Каждый отдельный показатель оценивается читателями по 5-балльной шкале целыми числами от 1 до 5. Аналитики, составляющие формулу рейтинга, считают, что объективность ценится втрое, а информативность публикаций − вдвое дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид R 2 In Op 3 Tr Q . A Каким должно быть число A , чтобы издание, у которого все оценки наибольшие, получило бы рейтинг 1? 66. Прототип задания 11 (№ 319860) Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности In , оперативности Op , объективности публикаций Tr , а также качества сайта Q . Каждый отдельный показатель оценивается читателями по 5-балльной шкале целыми числами от -2 до 2. Аналитики, составляющие формулу рейтинга, считают, что объективность ценится втрое, а информативность публикаций − впятеро дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид R 5 In Op 3 Tr Q . A Если по всем четырем показателям какое-то издание получило одну и ту же оценку, то рейтинг должен совпадать с этой оценкой. Найдите число A , при котором это условие будет выполняться.
| Ответы | |||||||
| 1. | 25 | 18. | 36 | 35. | 100 | 52. | 60 |
| 2. | 5000 | 19. | 7 | 36. | 0,2 | 53. | 60 |
| 3. | 1 | 20. | 4 | 37. | 30 | 54. | 60 |
| 4. | 6 | 21. | 55 | 38. | 0,125 | 55. | 30 |
| 5. | 1,2 | 22. | 120 | 39. | 30 | 56. | 60 |
| 6. | 2 | 23. | 10 | 40. | 2 | 57. | 45 |
| 7. | 50 | 24. | 400 | 41. | 0,05 | 58. | 60 |
| 8. | 20 | 25. | 18 | 42. | 2 | 59. | 0,5 |
| 9. | 90 | 26. | 2,5 | 43. | 30 | 60. | 0,5 |
| 10. | 2 | 27. | 5 | 44. | 2 | 61. | 0,67 |
| 11. | 20 | 28. | 390 | 45. | 6 | 62. | 0,00125 |
| 12. | 30 | 29. | 751 | 46. | 30 | 63. | 0,4 |
| 13. | 2 | 30. | 5000 | 47. | 30 | 64. | 0,71 |
| 14. | 5 | 31. | 180000 | 48. | 50 | 65. | 35 |
| 15. | 2 | 32. | 1,25 | 49. | 30 | 66. | 10 |
| 16. | 2 | 33. | 1,4 | 50. | 30 | ||
| 17. | 4000 | 34. | 7 | 51. | 15 | ||
| 10 |
Все прототипы заданий №12 2015 года 1. Прототип задания 12 (№ 27064) Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы. 6. Прототип задания 1 2 (№ 27069) Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
2. Прототип задания 12 (№ 27065) Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен 
3 , а высота равна 2. 7. Прототип задания 1 2 (№ 27070) Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
3. Прототип задания 12 (№ 27066) Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен 
3 , а высота равна 2. 8. Прототип задания 1 2 (№ 27083) Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.
4. Прототип задания 12 (№ 27067) Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности. 9. Прототип задания 1 2 (№ 27084) Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны 
3 . 5. Прототип задания 12 (№ 27068) Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы. 1
Источник: studfile.net
Сколько секций радиаторов нужно на 1 м² отапливаемой площади
Правильный расчёт секций радиаторов отопления — довольно важная задача для каждого домовладельца. Если будет использовано недостаточное количество секций, помещение не прогреется во время зимних холодов, а приобретение и эксплуатация слишком больших радиаторов повлечёт неоправданно высокие расходы на отопление. В статье мастер сантехник расскажет, сколько секций радиаторов нужно на 1 квадратный метр отапливаемой площади.
Как рассчитывать, сколько секций радиаторов нужно на 1 м²
Существует несколько доступных способов подсчитать объем радиатора с теплоносителем:
- Формулы;
- Таблицы;
- Компьютерные программы.
Каждый должен понимать, что у батарей из разных материалов отличается КПД, в плане теплоотдачи. Конечно, тепловая мощность радиаторов является одним из важнейших факторов для расчетов, но не определяющим.
На сегодня выпускаются:
Есть различные способы расчета, чтобы уменьшить погрешность, обычно считают:
- По площади пола;
- По объему помещения (высота потолков);
- По суммарным факторам.
Если использовать практику отопления городских квартир, с учетом того, что на 18 «квадратов» зала используется радиатор из 10 секций, вносятся логические корректировки:
- В Средней полосе России тепло обеспечивает 11-12 секций на комнату с невысокими потолками, в Сибири и Зауралье требуется 14-16 на такой же метраж. В Краснодарском крае зимой не холодно, хватит и 9-10 секций.
- Чугунные батареи на 8 сегментов имеют достаточную теплоотдачу, чтобы обогреть небольшую спальню (120-150 ватт на 1 секцию). Количество секций биметаллических радиаторов будет меньше, они имеют выше КПД, алюминиевые – ниже. Соответственно, для стандартной комнаты в 18-20 квадратных метров нужно 2 радиатора из чугуна по 8 секций или 1 биметаллический блок из 12 частей.
- Угловые комнаты с 1-2 внешними стенами без внутреннего и внешнего утепления вносят свои коррективы. Почти половина тепла теряется, особенно при резком похолодании, количество секций должно быть на 25-30% больше.
Существует ряд других факторов, вносящих корректировки в расчеты:
- Тип теплоносителя (пар, вода, антифриз);
- Количество внешних и внутренних стен;
- С чем граничит внешняя поверхность пола и потолка (чердак, подвал, жилые комнаты);
- Высота потолков (стандарт 2,7-3 м), бывают комнаты большего объема;
- Теплопроводность материала труб и батарей, на который влияет даже количество слоев краски и ее тип;
- Теплоизоляция стен;
- Количество окон, выходящих на разные стороны света;
- Продолжительность зимнего периода (климатический показатель);
- Предельная амплитуда температур в зимнее время;
- Старые деревянные окна или современные двойные стеклопакеты (последние максимально сохраняют тепло в помещениях);
- Схема подключения радиатора;
- Наличие теплого подъезда, мощной вентиляции, потребность в частом проветривании тоже влияет на выбор мощности системы отопления;
- Радиатор, закрываемый декоративным щитом или экраном для эстетики или в целях безопасности маленьких детей, теплоотдачу снижает на 10-15%. Напротив, фольгированное покрытие ниши для батарей способствует сохранению тепла.
Решая, какие радиаторы лучше для квартиры, предпочтительнее выбирать приборы, у которых отдача тепла больше.
Какие показатели еще учитываются в компьютерных программах
Существуют готовые таблицы, по которым можно определить потребность в количестве батарей для отопления своего помещения. Но это лишь приблизительно. Вот некоторые данные, которые должны вноситься в специальные компьютерные программы для определения количества секций радиаторов:
- Где находится квартира – на средних или крайних этажах.
- Куда выходят внешние стены – север и северо-восток самые холодные, юг и юго-запад немного прогреваются даже в морозную погоду.
- Второе (третье) окно увеличивает потребность в дополнительном многосекционном радиаторе, на 20% увеличивается необходимость дополнительного объема при больших незанавешенных окнах.
- Торцевые и угловые комнаты намного холоднее.
- Утепление внешних стен и внутренняя облицовка (натуральное дерево, другие сберегающие тепло покрытия).
- Панельный дом, кирпичный, литой или деревянный (если в панельном нужно 11 секций, то в деревянном достаточно 9).
- Средняя зимняя температура определяет коэффициент корректировки.
- Высота потолка в комнате (натяжные и многоуровневые конструкции тоже дают погрешность).
- Отапливается ли помещение над комнатой и под ней.
Как рассчитывать показатели по формулам
Произвести расчёты можно несколькими способы, в каждом из которых используются определённые параметры.
Расчет количества секций радиатора по площади помещения
