Для получения направленного пучка света в проекторе в качестве отражателя используется вогнутое сферическое зеркало диаметром с фокусным расстоянием . На каком расстоянии от зеркала нужно расположить точечный источник, чтобы лучи, отразившись от зеркала, образовали на стене светлое пятно диаметром ? Расстояние от зеркала до стены .
Возможны два решения задачи.
1. Пусть изображение источника находится перед стенкой (см. рис.). Тогда
По формуле сферического зеркала найдем
2. Изображение источника можно располагаться за стенкой. В этом случае имеем
С помощью формулы сферического зеркала найдем
| 1 из 2 |
Источник: physics.ru
Задача про периметр и забывчивого монтажника
Одному монтажнику поставили задачу — подготовить кабель для камер видеонаблюдения на первом этаже здания. Само здание прямоугольное, а стены между комнатами делят этаж на 4 комнаты-прямоугольника. В техническом условии было написано, что кабель в каждой комнате должен идти точно по периметру стен, поэтому монтажник измерил периметр каждой комнаты и записал всё на листочке. Но он спешил, поэтому в магазине обнаружил, что забыл записать периметр последней комнаты:
Как быстро решать задачи на проценты

Помогите монтажнику найти периметр последнего прямоугольника, чтобы ему не пришлось лишний раз возвращаться на объект.
Обозначим буквами стороны каждого прямоугольника:
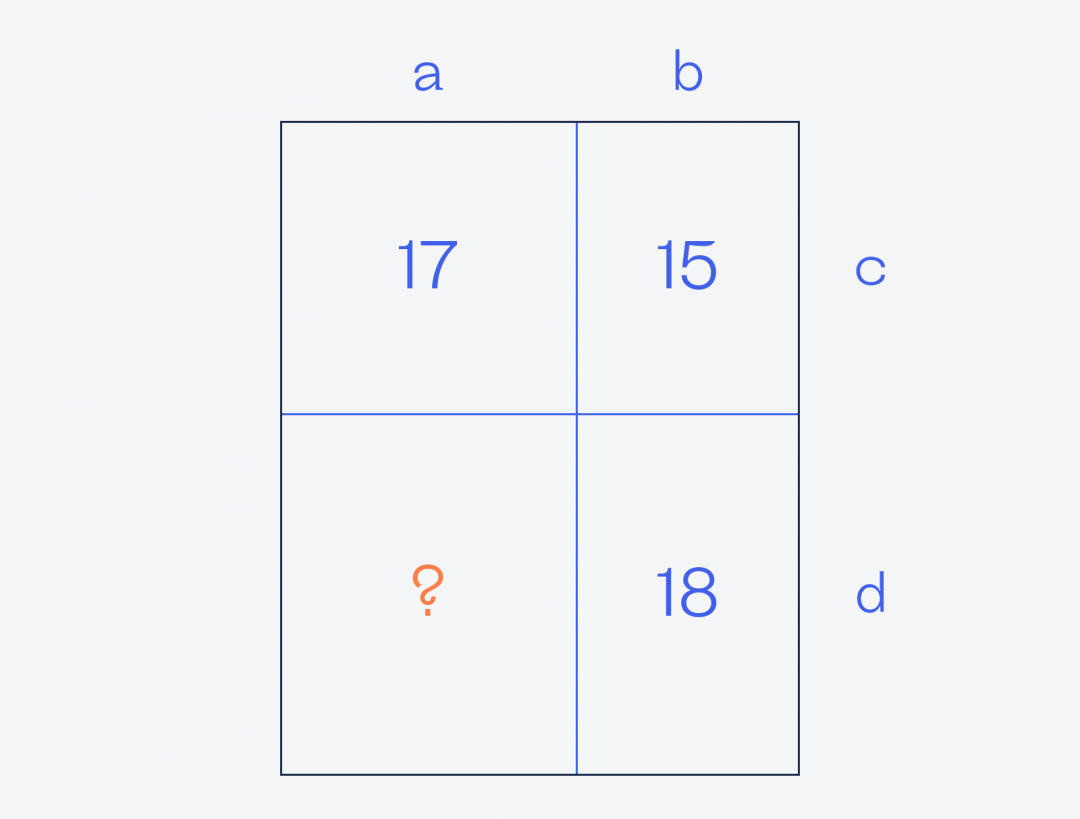
Теперь, когда у нас есть обозначения сторон, запишем то, что нам уже известно:
Периметр последнего прямоугольника равен 2a + 2d — эту сумму мы и будем искать в решении.
Возьмём первое уравнение и посчитаем, чему равно 2c, чтобы подставить это во второе уравнение:
2c = 17 − 2a → подставляем во второе уравнение
2b + 17 − 2a = 15 → 2b − 2a = 15 − 17 → 2b − 2a = −2
Теперь отсюда выясним, чему равно 2b, и подставим это в третье уравнение:
2b − 2a = −2 → 2b = 2a − 2 → подставляем в третье уравнение:
Но периметр последней комнаты как раз равен 2a + 2d, а значит, он равен 20.
Источник: thecode.media
Обобщающий урок геометрии по теме «Решение задач на применение признаков равенства треугольников» в 7-м классе

Дидактическая задача урока: систематизировать знания и умения учащихся решать задачи на применение признаков равенства треугольников, уметь делать обобщение изучаемых фактов.
Проектор-приложение
Цели:
- Повторить и закрепить знание учащимися формулировок признаков равенства треугольников.
- Формирование умений:
— доказывать их равенство;
— делать выводы о равенстве некоторых их элементов.
- Тренировать способность решать задачи, используя признаки равенства треугольников
- Воспитывать аккуратность и прилежание.
- Прививать положительное отношение к знаниям, к процессу учения.
- Формировать самостоятельность и умение делать самооценку.
- Развивать творческие способности, познавательную активность.
- Развивать умение решать задачи по готовым чертежам, развивать логическое мышление.
- Учить разрешению проблемы, частично-поисковой деятельности учащихся.
- Развивать внимание, слуховую и зрительную память.
- Формировать математическую речь учащихся.
Тип урока: урок систематизации и обобщения знаний, умений, навыков.
Методическое обеспечение урока:
- Компьютер
- Мультимедиа-проектор
- Листы с печатной основой – карточки с тестами на знание признаков равенства треугольников, карточки с заданиями для работы на уроке.
Ход урока
1. Организационный момент.
Проверка готовности учащихся к уроку. Эмоциональный настрой учащихся.
2. Актуализация знаний.
Фронтальная работа с классом.
— Какую геометрическую фигуру изучаем? (Треугольник).
— Проверим, что вы уже знаете об этой фигуре.
— Какие вы знаете виды треугольников? (Остроугольный, прямоугольный, тупоугольный, равнобедренный и равносторонний)
— Какие треугольники называются равными? (Которые можно совместить при наложении)
— Что помогает определить равенство треугольников? (Признаки равенства треугольников).
— Какие признаки равенства треугольников вы знаете? Посмотрите на экран.
— Какой признак равенства треугольников вы здесь видите?
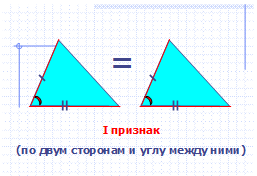
I признак равенства треугольников (по двум сторонам и углу между ними)
— Какой признак равенства треугольников вы видите здесь?
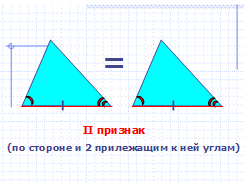
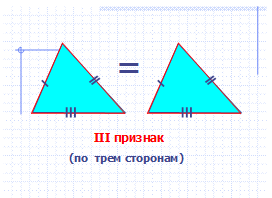
II признак равенства треугольников (по стороне и 2 прилежащим к ней углам)
— Какой признак равенства треугольников вы здесь видите?
III признак равенства треугольников (по трем сторонам)
Выполнение теста «Верно-неверно».
На столах у каждого из вас лежат опросные листы. Мы будем работать с ними на протяжении всего урока. Выполним следующее задание №1. Если вы согласны с утверждением ставите +, если нет, ставите –.
Учащимся дается время (3 мин.) на выполнение задания.
Слайды 5-6.
Утверждение
Если в треугольнике две стороны равны, то треугольник называется равнобедренным.
Отрезок, соединяющий вершину треугольника с противоположной стороной, называется медианой треугольника.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Если сторона и два угла одного треугольника равны соответственно стороне и двум углам другого треугольника, то такие треугольники равны.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
В треугольнике углы при основании равны.
Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой.
Если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники равны.
После учитель вместе с учащимися осуществляет проверку, используя проектор.
1. Если в треугольнике две стороны равны, то треугольник называется равнобедренным. (+)
2. Отрезок, соединяющий вершину треугольника с противоположной стороной, называется медианой треугольника. (–) (пропущено слово: середина).
3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. (+)
4. Если сторона и два угла одного треугольника равны соответственно стороне и двум углам другого треугольника, то такие треугольники равны. (–) (Правильно: два угла, прилежащих к ней).
5. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. (+)
6. В треугольнике углы при основании равны. (–) (Пропущено слово: равностороннем или равнобедренном).
7. Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой. (+)
8. Если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники равны. (–)
— Переведите полученные баллы в отметку (на листах контроля сказано, как это сделать).
Слайд 7.
8 баллов – отметка «5»
7–6 баллов – отметка «4»
5–4 баллов – отметка «3»
Менее 4 баллов – «будем работать дальше»
Поставьте полученную отметку в лист контроля.
— Поднимите руки те, кто получил – 5, кто получил – 4, кто получил – 3. С остальными будем работать дальше.
3. Формулировка темы и целей урока.
— Ребята, первый год вы изучаете предмет геометрия и поняли, что предметом изучения этого раздела математики является решение задач на основе изученных определений, свойств и теорем. Но чтобы хорошо научиться решать задачи, что для этого выполнять? ( Дети отвечают).
Слайд 8.
— А ещё известный педагог и математик Дъёрдь Пойа (1887-1985) сравнивал умение решать задачи с умением научиться плавать.
Если вы хотите научиться плавать, то смело входите в воду,
а если хотите научиться решать задачи, то решайте их.
(Д.Пойа)
Дъёрдь Пойа, венгерский, швейцарский и американский математик, много работал со школьными учителями математики и внёс большой вклад в популяризацию науки. Он написал несколько книг о том, как решают задачи и как надо учить решать задачи
— Сформулируйте цели урока. Чем мы будем заниматься и чего должны достичь к концу урока? (Учащиеся формулируют цели – Решение задач на применение признаков равенства треугольников) Слайд 9.
4. Решение задач.
— В геометрии очень важно уметь смотреть и видеть, замечать и отмечать различные особенности геометрических фигур.
«Если знаешь — докажи». Выполнение задания по готовым чертежам (устная работа с классом).
Следующее задание. Ваша задача по готовому чертежу доказать равенство треугольников.
Слайд 13. № 4.
— Ребята! Сейчас в своей работе вы использовали такой приём, как доказательство. Эта форма работы вам уже известна. А до VI века с доказательством люди вообще были не знакомы. Первым учёным, который стал рассуждать, доказывать, был Фалес Милетский.
Фалес считается одним из семи мудрецов, оказавших большое влияние на жизнь древних греков. Одним из самых известных его высказываний было «Познай самого себя». Именно Фалесу Милетскому приписывают доказательство о равенстве двух треугольников, имеющих равными сторону и два прилежащих к ней угла (второй признак равенства треугольников).
— Признаки равенства треугольников имели издавна важнейшее значение в геометрии, так как доказательства многочисленных теорем сводилось к доказательству равенства тех или иных треугольников.
6. Решение задач по готовому чертежу (с записью доказательства в опросных листах).
Слайд 15.
| № 2.1 |
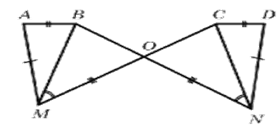 |
Дано: МО=ОN, АМ=DN, АВ=СD, Доказать: ∆АВМ=∆DСN
Вопросы к учащимся:
- Равенство каких треугольников мы можем доказать? (∆МВО=∆NСО по стороне и двум прилежащим к ней углам.)
- Из равенства треугольников ∆МВО=∆NСО какие элементы мы возьмем? ( В равных треугольниках соответственные стороны равны, значит МВ=NС)
- Теперь мы сможем доказать равенство ∆АВМ=∆DСN? (Треугольники равны по трем сторонам)
— Запишите доказательство к этой задаче с обоснованием каждого шага (доказательство записать в опросный лист)Слайд 16.
| № 2.2 |
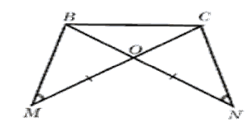 |
Дано: МО=ОN, угол М равен углу N
Доказать: ∆ВОС – равнобедренный
Вопросы к учащимся:
- Какой треугольник называется равнобедренным? (Равнобедренный треугольник – это треугольник, у которого две стороны равны.)
- Как доказать равенство сторон ВО и ОС? (Из равенства треугольников ∆МВО и ∆NСО)
- Правильно, сначала нужно доказать равенство ∆МВО=∆NСО. Как это сделать? (∆МВО=∆NСО по стороне и двум прилежащим к ней углам. В равных треугольниках соответственные стороны равны, значит ВО=ОС, значит ∆ВОС — равнобедренный, т.к. у него две стороны равны.)
— Запишите доказательство к этой задаче с обоснованием каждого шага (доказательство записать в опросный лист)
№ 4 (устно)
Слайд 17.
Найти : FK
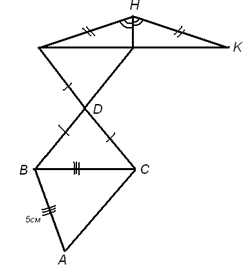
Вопросы к учащимся:
— Что можно найти, зная, что AB= 5 см и AB=BC? (ВС=5 см)
- Равенство каких треугольников мы можем доказать? (∆DВC=∆DFO по двум сторонам и углу между ними.)
- Из равенства треугольников ∆DВC=∆DFO какие элементы мы возьмем? ( В равных треугольниках соответственные стороны равны, значит BC=FO=5 см)
- Что вы можете сказать о ∆FHK? (∆FHK – равнобедренный, HO – биссектриса ∆FHK, а значит и медиана ∆FHK, т.е. FO=KO=5 см. Тогда FK=10см)
Учащимся раздаются готовые чертежи геометрических фигур. Нужно исследовать: отметить равные отрезки и углы, выписать пары равных треугольников. Работают в опросных листах, затем следует проверка. Учитель оказывает индивидуальную помощь слабым учащихся. Можно друг у друга спросить совета.
Закрепляется навык учащихся доказывать равенство треугольников, используя признаки.
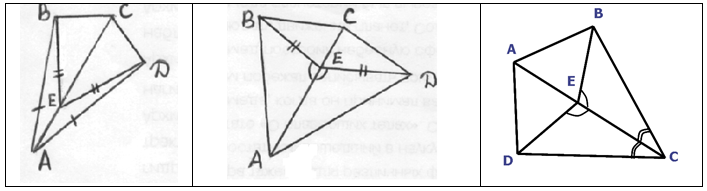
Проверка осуществляется с помощью проектора. Слайды 18–20.
6. Подведение итогов урока.
— Какие цели ставили?
— Достигли их или нет
Слайд 21.
Продолжите предложение:
- Мы изучили признаки равенства треугольников для того, чтобы…
- Мне стало понятно…
- Я понял, что смогу …
- У меня получилось …
- На следующих уроках по геометрии…
Выставление оценок учителем.
7. Домашнее задание (учебник Л.С. Атанасян, В.Ф.Бутузов и др. «Геометрия 7-9»,М., Просвещение 2010)
№ 134, № 138 (а)
Список использованной литературы
1. Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7- 9 классы. – М.: Просвещение, 2010.
2. Атанасян Л.С., Бутузов В.Ф., Глазков Ю.А. и др. Геометрия. Рабочая тетрадь для 7 класса. – М.: Просвещение, 2009.
3. Жохов В.И., Карташнва Г.Д., Крайнева Л.Б. Уроки геометрии в 7-9 классах: Методические рекомендации для учителя к учебнику Атанасяна Л.С. и др. – М.: Вербум-М, 2004.
4. Атанасян Л.С., Бутузов В.Ф., Глазков Ю.А. и др. Изучение геометрии в 7, 8, 9 классах: Метод. Рекомендации к учебнику: Книга для учителя. – М.: Просвещение, 2009.
5. Зив Б.Г., Мейлер В.М. Дидактические материалы по геометрии 7 класс. – М.: Просвещение, 2006.
Источник: open-lesson.net