Как мы знаем из предыдущей темы, для более подробного разглядывания объекта нужно увеличить угол зрения. Тогда изображение объекта на сетчатке будет крупнее, и это приведёт к раздражению большего числа нервных окончаний зрительного нерва; в мозг направится большее количество визуальной информации, и мы сможем увидеть новые детали рассматриваемого объекта.
Почему угол зрения бывает малым? На то есть две причины: 1) объект сам по себе имеет малый размер; 2) объект, хотя и достаточно велик по размерам, но расположен далеко.
Оптические приборы — это приспособления для увеличения угла зрения. Для рассматривания малых объектов используются лупа и микроскоп. Для рассматривания далёких объектов применяются зрительные трубы (а также бинокли, телескопы и т. д.)
Невооружённый глаз.
Начинаем с рассматривания мелких объектов невооружённым глазом. Здесь и далее глаз считается нормальным. Напомним, что нормальный глаз в ненапряжённом состоянии фокусирует на сетчатке параллельный пучок света, а расстояние наилучшего зрения для нормального глаза равно см.
Ход лучей через линзы
Пусть небольшой предмет размером находится на расстоянии наилучшего зрения от глаза (рис. 1 ). На сетчатке возникает перевёрнутое изображение предмета, но, как вы помните, это изображение затем вторично переворачивается в коре головного мозга, и в результате мы видим предмет нормально — не вверх ногами.
 |
| Рис. 1. Рассматривание мелкого предмета невооружённым глазом |
Ввиду малости предмета угол зрения также является малым. Напомним, что малый угол (в радианах) почти не отличается от своего тангенса: . Поэтому:
Если r расстояние от оптического центра глаза до сетчатки, то размер изображения на сетчатке будет равен:
Из (1) и (2) имеем также:
Как известно, диаметр глаза составляет около 2,5 см, так что . Поэтому из (3) следует, что при рассматривании мелкого предмета невооружённым глазом изображение предмета на сетчатке примерно в 10 раз меньше самого предмета.
Лупа.
Укрупнить изображение объекта на сетчатке можно с помощью лупы (увеличительного стекла).
Лупа — это просто собирающая линза (или система линз); фокусное расстояние лупы обычно находится в диапазоне от 5 до 125 мм. Предмет, разглядываемый через лупу, помещается в её фокальной плоскости (рис. 2 ). В таком случае лучи, исходящие из каждой точки предмета, после прохождения лупы становятся параллельными, и глаз фокусирует их на сетчатке, не испытывая напряжения.
 |
| Рис. 2. Рассматривание предмета через лупу |
Линзы, оптическая сила линзы, формула тонкой линзы.Построение изображений в линзах. 8 класс.
Теперь, как видим, угол зрения равен . Он также мал и приблизительно равен своему тангенсу:
Размер l изображения на сетчатке теперь равен:
Как и на рис. 1, красная стрелочка на сетчатке также направлена вниз. Это означает, что (с учётом вторичного переворачивания изображения нашим сознанием) в лупу мы видим неперевёрнутое изображение предмета.
Увеличение лупы — это отношение размера изображения при использовании лупы к размеру изображения при рассматривании предмета невооружённым глазом:
Подставляя сюда выражения (6) и (3) , получим:
Например, если фокусное расстояние лупы равно 5 см, то её увеличение . При рассматривании через такую лупу объект кажется в пять раз больше, чем при рассматривании его невооружённым глазом.
Подставим также в формулу (7) соотношения (5) и (2) :
Таким образом, увеличение лупы есть угловое увеличение: оно равно отношению угла зрения при рассматривании объекта через лупу к углу зрения при рассматривании этого объекта невооружённым глазом.
Отметим, что увеличение лупы есть величина субъективная — ведь величина в формуле (8) есть расстояние наилучшего зрения для нормального глаза. В случае близорукого или дальнозоркого глаза расстояние наилучшего зрения будет соответственно меньше или больше.
Из формулы (8) следует, что увеличение лупы тем больше, чем меньше её фокусное расстояние. Уменьшение фокусного расстояния собирающей линзы достигается за счёт увеличения кривизны преломляющих поверхностей: линзу надо делать более выпуклой и тем самым уменьшать её размеры. Когда увеличение достигает 40–50, размер лупы становится равным нескольким миллиметрам. При ещё меньших размерах лупы пользоваться ей станет невозможно, поэтому считается верхней границей увеличения лупы.
Микроскоп.
Во многих случаях (например, в биологии, медицине и т. д.) нужно наблюдать мелкие объекты с увеличением в несколько сотен. Лупой тут не обойдёшься, и люди прибегают к помощи микроскопа.
Микроскоп содержит две собирающие линзы (или две системы таких линз) — объектив и окуляр. Запомнить это просто: объектив обращён к объекту, а окуляр — к глазу (к оку).
Идея микроскопа проста. Рассматриваемый объект находится между фокусом и двойным фокусом объектива, так что объектив даёт увеличенное (действительное перевёрнутое) изображение объекта. Это изображение располагается в фокальной плоскости окуляра и затем рассматривается в окуляр как в лупу. В результате удаётся достичь итогового увеличения, гораздо большего 50.
Ход лучей в микроскопе показан на рис. 3 .
 |
| Рис. 3. Ход лучей в микроскопе |
Обозначения на рисунке понятны: — фокусное расстояние объектива — фокусное расстояние окуляра — размер объекта; — размер изображения объекта, даваемого объективом. Расстояние между фокальными плоскостями объектива и окуляра называется оптической длиной тубуса микроскопа.
Обратите внимание, что красная стрелочка на сетчатке направлена вверх. Мозг вторично перевернёт её, и в результате объект при рассмотрении в микроскоп будет казаться перевёрнутым. Чтобы этого не происходило, в микроскопе используются промежуточные линзы, дополнительно переворачивающие изображение.
Увеличение микроскопа определяется точно так же, как и для лупы: . Здесь, как и выше, и — размер изображения на сетчатке и угол зрения при рассматривании объекта в микроскоп, и — те же величины при рассматривании объекта невооружённым глазом.
Имеем по-прежнему , а угол , как видно из рис. 3 , равен:
Деля на , получим для увеличения микроскопа:
Это, разумеется, не окончательная формула: в ней присутствуют и (величины, относящиеся к объекту), а хотелось бы видеть характеристики микроскопа. Ненужное нам отношение мы устраним с помощью формулы линзы.
Для начала ещё раз посмотрим на рис. 3 и используем подобие прямоугольных треугольников с красными катетами и :
Здесь — расстояние от изображения до объектива, — a — расстояние от объекта h до объектива. Теперь привлекаем формулу линзы для объектива:
из которой получаем:
и это выражение мы подставляем в (9) :
Вот это и есть окончательное выражение для увеличения, даваемого микроскопом. Например, если фокусное расстояние объектива равно см, фокусное расстояние окуляра , а оптическая длина тубуса см, то согласно формуле (10)
Сравните это с увеличением одного только объектива, которое вычисляется по формуле (8) :
Увеличение микроскопа в 10 раз больше!
Теперь мы переходим к объектам, которые достаточно крупны, но находятся слишком далеко от нас. Чтобы рассматривать их получше, применяются зрительные трубы — подзорные трубы, бинокли, телескопы и т. д.
Объективом зрительной трубы служит собирающая линза (или система линз) с достаточно большим фокусным расстоянием. А вот окуляром может быть как собирающая, так и рассеивающая линза. Соответственно имеются два вида зрительных труб:
-труба Кеплера — если окуляр является собирающей линзой;
-труба Галилея — если окуляр является рассеивающей линзой.
Рассмотрим подробнее, как работают эти зрительные трубы.
Труба Кеплера.
Принцип действия трубы Кеплера очень прост: объектив даёт изображение удалённого обекта в своей фокальной плоскости, а затем это изображение рассматривается в окуляр как в лупу. Таким образом, задняя фокальная плоскость объектива совпадает с передней фокальной плоскостью окуляра.
Ход лучей в трубе Кеплера изображён на рис. 4 .
 |
| Рис. 4 |
Объектом служит далеко расположенная стрелка , направленная вертикально вверх; она не показана на рисунке. Луч из точки идёт вдоль главной оптической оси объектива и окуляра. Из точки идут два луча, которые ввиду удалённости объекта можно считать параллельными.
В результате изображение нашего объекта, даваемое объективом, расположено в фокальной плоскости объектива и является действительным, перевёрнутым и уменьшенным. Размер изображения обозначим .
Невооружённым глазом объект виден под углом . Согласно рис. 4 :
где — фокусное расстояние объектива.
Изображение объекта мы видим в окуляр под углом , который равен:
где — фокусное расстояние окуляра.
Увеличение зрительной трубы — это отношение угла зрения при наблюдении в трубу к углу зрения при наблюдении невооружённым глазом:
Согласно формулам (12) и (11) получаем:
Например, если фокусное расстояние объектива равно 1 м, а фокусное расстояние окуляра равно 2 см, то увеличение зрительной трубы окажется равным: .
Ход лучей в трубе Кеплера принципиально тот же, что и в микроскопе. Изображением объекта на сетчатке также будет стрелочка, направленная вверх, и поэтому в трубе Кеплера мы увидим объект перевёрнутым. Во избежании этого в пространстве между объективом и окуляром ставят специальные оборачивающие системы линз или призм, которые ещё раз переворачивают изображение.
Труба Галилея.
Галилей изобрёл свой телескоп в 1609 году, и его астрономические открытия потрясли современников. Он обнаружил спутники Юпитера и фазы Венеры, разглядел лунный рельеф (горы, впадины, долины) и пятна на Солнце, а сплошной с виду Млечный Путь оказался скоплением звёзд.
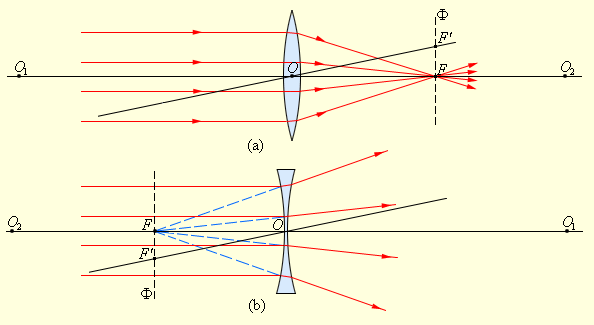
Окуляром трубы Галилея служит рассеивающая линза; задняя фокальная плоскость объектива совпадает с задней фокальной плоскостью окуляра (рис. 5 ).
 |
| Рис. 5. |
Если бы окуляра не было, то изображение удалённой стрелки находилось бы в
фокальной плоскости объектива. На рисунке это изображение показано пунктиром — ведь в реальности его там нет!
А нет его там потому, что лучи от точки , которые после прохождения объектива стали сходящимися к точке , не доходят до и попадают на окуляр. После окуляра они вновь становятся параллельными и поэтому воспринимаются глазом без напряжения. Но теперь мы видим изображение объекта под углом , который больше угла зрения при рассматривании объекта невооружённым глазом.
и для увеличения трубы Галилея мы получаем ту же формулу (13) , что и для трубы Кеплера:
Заметьте, что при том же увеличении труба Галилея меньше размером, чем труба Кеплера. Поэтому одно из основных применений трубы Галилея — театральные бинокли.
В отличие от микроскопа и трубы Кеплера, в трубе Галилея мы видим объекты неперевёрнутыми. Почему?
Спасибо за то, что пользуйтесь нашими публикациями. Информация на странице «Оптические приборы.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена: 07.07.2023
Источник: ege-study.ru
Что такое линза в проекторе?
Линза или по-другому слайд, это информационная часть проектора. Прозрачная пластина с рисунком, который проецируется аппаратурой и формирует изображение проекции.
Уже по названию понятно, что они изготавливаются из стекла. Мы изготавливаем линзы (слайды) из закаленного стекла. Выполненные из стекла слайды самые долговечные и надежные. У них самая лучшая резкость и цветовая насыщенность. Они не выгорают.
Качество изображения таких линз лучшее.
Тонкие линзы
В тонкой линзе главная оптическая ось пересекается в одной точке – оптическом центре линзы O . Световой луч проходит через оптический центр линзы, не отклоняясь от своего первоначального направления.
Определение 11
Величина D – это оптическая сила линзы, равная обратному фокусному расстоянию.
Диоптрия ( д п т р ) является единицей измерения оптической силы, фокусное расстояние которой равно 1 м : 1 д п т р = м — 1 .
Формула тонкой линзы аналогична формуле сферического зеркала. Можно вывести ее для параксиальных лучей из подобия треугольников на рисунках 3 . 3 . 3 либо 3 . 3 . 4 .
Фокусное расстояние линз записывается с определенными знаками: собирающая линза F > 0 , рассеивающая F < 0 .
Величина d и f тоже подчиняются определенным знакам:
- d > 0 и f > 0 – применительно к действительным предметам (то есть реальным источникам света) и изображений;
- d < 0 и f < 0 – применительно к мнимым источникам и изображениям.
Для случая на рисунке 3 . 3 . 3 F > 0 (линза собирающая), d = 3 F > 0 (действительный предмет).
Из формулы тонкой линзы получаем: f = 3 2 F > 0 , означает, что изображение действительное.
Для случая на рисунке 3 . 3 . 4 F < 0 (линза рассеивающая), d = 2 | F | >0 (действительный предмет), справедлива формула f = — 2 3 F < 0 , следовательно, изображение мнимое.
Линейные размеры изображения зависят от положения предмета по отношению к линзе.
Линейное увеличение линзы Г – это отношение линейных размеров изображения h ‘ и предмета h .
Величину h ‘ удобно записывать со знаками плюс или минус, в зависимости от того, прямое оно или перевернутое. Она всегда положительна. Потому для прямых изображений применяется условие Γ > 0 , для перевернутых Γ < 0 . Из подобия треугольников на рисунках 3 . 3 . 3 и 3 . 3 . 4 нетрудно вывести формулу для расчета линейного увеличения тонкой линзы:
В примере с собирающей линзой на рисунке 3 . 3 . 3 при d = 3 F > 0 , f = 3 2 F > 0 .
В примере с рассеивающей линзой на рисунке 3 . 3 . 4 при d = 2 | F | > 0 , справедлива формула f = — 2 3 F < 0 ; значит, Г = 1 3 >0 – изображение прямое и уменьшенное в три раза.
Оптическая сила D линзы находится в зависимости от радиусов кривизны R 1 и R 2 , ее сферических поверхностей, а также и от показателя преломления n материала линзы. В теории оптики имеет место следующее выражение:
D = 1 F = ( n — 1 ) 1 R 1 + 1 R 2 .
Выпуклая поверхность имеет положительный радиус кривизны, а вогнутая поверхность – отрицательным. Данная формула применима в изготовлении линз с заданной оптической силой.
Многие оптические приборы устроены таким образом, что свет последовательно проходит через 2 или несколько линз. Изображение предмета от 1 -й линзы служит предметом (действительным или мнимым) для 2 -й линзы, выстраивающей, в свою очередь, 2 -е изображение предмета, которое также может быть действительным либо мнимым. Расчет оптической системы из 2 -х тонких линз состоит в
2 -кратном применении формулы линзы, причем расстояние d 2 от 1 -го изображения до 2 -й линзы следует предложить равное величине l – f 1 , где l – это расстояние между линзами.
Астрономическая труба Кеплера и земная труба Галилея
Рассмотрим частный случай – телескопический ход лучей в системе из 2 -х линз, когда и предмет, и 2 -е изображение расположены на бесконечно больших расстояниях друг от друга. Телескопический ход лучей выполняется в зрительных трубах: земной трубе Галилея и астрономической трубе Кеплера.
Тонкая линза имеет некоторые недостатки, которые не позволяют получать изображения высокого разрешения.
Аберрация – это искажение, которое возникает в процессе формирования изображения. В зависимости от расстояния, на котором проводится наблюдение, аберрации могут быть сферическими и хроматическими.
Смысл сферической аберрации в том, что при широких световых пучках лучи, находящиеся на далеком расстоянии от оптической оси, пересекают ее не в месте фокуса. Формула тонкой линзы действует лишь для лучей, которые находятся близко к оптической оси. Изображение удаленного источника, которое создается широким пучком лучей, преломленных линзой, размыто.
Смысл хроматической аберрации в том, что на показатель преломления материала линзы влияет длина световой волны λ . Данное свойство прозрачных сред называют дисперсией. Фокусное расстояние линзы различно для света с различными длинами волн. Данный факт приводит к размытию изображения при излучении немонохроматического света.
Современные оптические приборы оснащены не тонкими линзами, а сложными линзовыми системами, в которых есть возможность исключить некоторые искажения.
В таких приборах, как фотоаппараты, проекторы и т.д., используются собирающие линзы для формирования действительных изображений предметов.
Что представляет собой фотоаппарат
Определение 15
Фотоаппарат – это замкнутая светонепроницаемая камера, в которой изображение запечатленных предметов создается на пленке системой линз – объективом. На время экспозиции объектив открывается и закрывается с помощью специального затвора.
Особенность работы фотоаппарата в том, что на плоской фотопленке получаются довольно резкие изображения предметов, которые находятся на различных расстояниях. Резкость меняется вследствие перемещения объектива относительно фотопленки. Изображения точек, которые не лежат в плоскости резкого наведения, выходят на снимках размытыми в виде рассеянных кружков. Размер d данных кружков можно уменьшить методом диафрагмирования объектива, то есть уменьшения относительного отверстия a F , как показано на рисунке 3 . 3 . 5 . Это в результате увеличивает глубину резкости.
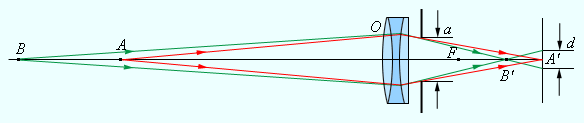
Рисунок 3 . 3 . 5 . Фотоаппарат.
С помощью проекционного аппарата удается снять масштабные изображения. Объектив O проектора фокусирует изображение плоского предмета (диапозитив D ) на удаленном экране Э (рисунок 3 . 3 . 6 ). Система линз K (конденсор) используется для концентрации света источника S на диапозитиве. На экране воссоздается увеличенное перевернутое изображение. Масштаб проекционного устройства можно изменять, приближая или отдаляя экран и одновременно изменяя расстояние между диапозитивом D и объективом O .
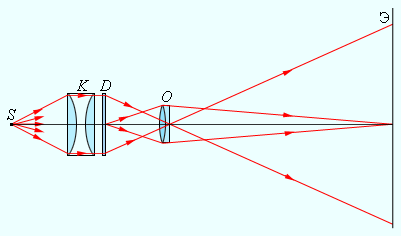
Рисунок 3 . 3 . 6 . Проекционный аппарат.
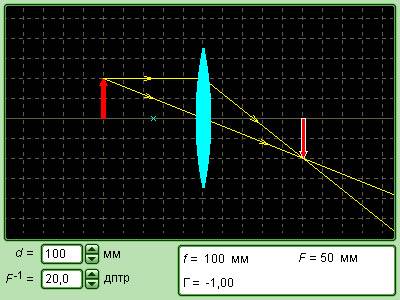
Рисунок 3 . 3 . 7 . Модель тонкой линзы.
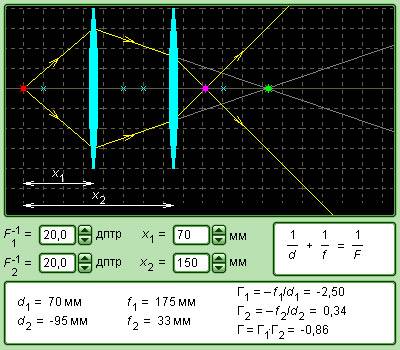
Рисунок 3 . 3 . 8 . Модель системы из двух линз.
Источник: zaochnik-com.com