На этом рисунке преобразование [math]displaystyle< P >[/math] является ортогональной проекцией на прямую [math]displaystyle< m >[/math] .
В линейной алгебре и функциональном анализе линейный оператор [math]displaystyle< P >[/math] , действующий в линейном пространстве, называется прое́ктором (а также опера́тором проеци́рования и проекцио́нным опера́тором) если [math]displaystyle< P^2=P >[/math] . Такой оператор называют идемпотентным.
Несмотря на свою абстрактность, это определение обобщает идею построения геометрической проекции.
В качестве определения можно использовать следующее свойство проектора: линейный оператор [math]displaystyle< P:Xto X >[/math] является проектором тогда и только тогда, когда существуют такие подпространства [math]displaystyle< U >[/math] и [math]displaystyle< V >[/math] пространства [math]displaystyle< X >[/math] , что [math]displaystyle< X >[/math] раскладывается в их прямую сумму, и при этом для любой пары элементов [math]displaystyle< uin U, vin V >[/math] имеем [math]displaystyle< P(u+v)=u >[/math] . Подпространства [math]displaystyle< U >[/math] и [math]displaystyle< V >[/math] — соответственно образ и ядро проектора [math]displaystyle< P >[/math] , и обозначаются [math]displaystyle< mathrmP >[/math] и [math]displaystyle< mathrmP >[/math] .
Что такое линейная алгебра, зачем нужна и как с ней работать? Душкин объяснит
В общем случае, разложение линейного пространства в прямую сумму не единственно. Поэтому, для подпространства [math]displaystyle< V >[/math] пространства [math]displaystyle< X >[/math] , вообще говоря, существует много проекторов, образ или ядро которых совпадает с [math]displaystyle< V >[/math] .
- 1 Свойства проекционных операторов
- 2 Комбинации проекторов
- 3 Примеры
- 4 Ортогональный проектор
- 5 Литература
Свойства проекционных операторов
- Пусть [math]displaystyle< I >[/math] — тождественный оператор. Если [math]displaystyle< P >[/math] — проектор, то [math]displaystyle< I-P >[/math] тоже проектор, причём [math]displaystyle< mathrm=mathrm>[/math] и [math]displaystyle< mathrm=mathrmP >[/math] .
- В конечномерном нормированном пространстве все проекционные операторы непрерывны.
- Для банахова же пространства проекционный оператор будет непрерывным, если его образ замкнут, при этом ядро проектора тоже окажется замкнутым. Таким образом, непрерывный проектор задаёт разложение пространства в прямую сумму замкнутых подпространств: [math]displaystyle < X=mathrmP oplus mathrm, P >[/math] .
- Собственными значениями проектора могут быть только 0 и 1. Соответствующими собственными подпространствами проектора будут его ядро и образ.
Комбинации проекторов
Пусть [math]displaystyle< P_1 >[/math] и [math]displaystyle< P_2 >[/math] — проекторы, заданные на векторном пространстве [math]displaystyle< X >[/math] , и проецирующие на подпространства [math]displaystyle< M_1 >[/math] и [math]displaystyle< M_2 >[/math] соответственно. Тогда
- [math]displaystyle< P_1+P_2 >[/math] — проектор на подпространстве [math]displaystyle< M_1oplus M_2 >[/math] , в том и только том случае, когда [math]displaystyle< P_1 P_2=P_2 P_1=0 >[/math] .
- [math]displaystyle< P_1-P_2 >[/math] является проектором тогда и только тогда, когда [math]displaystyle< P_1 P_2=P_2 P_1=P_2 >[/math] . [math]displaystyle< P_1-P_2 >[/math] проецирует на подпространство [math]displaystyle< M_1cap(Xominus M_2) >[/math] .
- Если [math]displaystyle< P_1P_2=P_2P_1=P >[/math] , то [math]displaystyle< P >[/math] — проектор на подпространство [math]displaystyle< M_1cap M_2 >[/math] .
Примеры
- Ортогональная проекция (см. ниже) точек [math]displaystyle< (x, y, z) >[/math] пространства [math]displaystyle< R^3 >[/math] на плоскость [math]displaystyle< Oxy >[/math] задаётся матрицей
Действует на точки она следующим образом:
Преобразование T является косоугольной проекцией вдоль k на прямую m. U=m и V=k.
- Простейший неортогональный проектор осуществляет косоугольную проекцию точек плоскости на прямую. Он задаётся матрицей:
Легко показать, что это действительно проектор:
[math]displaystyle < P^2 = begin0 1 end begin 0 1 end = begin 0 1 end = P. >[/math]
Проекция, задаваемая [math]displaystyle< P >[/math] , ортогональна, тогда и только тогда, когда [math]displaystyle< alpha = 0 >[/math] .
Ортогональный проектор
Если пространство [math]displaystyle< X >[/math] — гильбертово, то есть обладает скалярным произведением (а значит и понятием ортогональности), то можно ввести понятие ортогонального проектора.
Ортогональный проектор — это частный случай проектора, когда выше упомянутые подпространства [math]displaystyle< U >[/math] и [math]displaystyle< V >[/math] ортогональны друг другу, иными словами, когда [math]displaystyle< forall uin U, forall vin V >[/math] [math]displaystyle< (u,v)=0 >[/math] , или [math]displaystyle< ucdot v =0 >[/math] , или [math]displaystyle< uperp v =0 >[/math] . В этом случае проекция элемента [math]displaystyle< xin X >[/math] является ближайшим к нему элементом пространства [math]displaystyle< U >[/math] .
Литература
- Треногин В. А. Функциональный анализ. — М. : Наука, 1980. — 495 с.
- Халмош П. Конечномерные векторные пространства = Finite-dimensional vector spaces. — М. : Физматгиз, 1963. — 264 с.
Для улучшения этой статьи желательно:
- Проставить сноски, внести более точные указания на источники.
Источник: xn--h1ajim.xn--p1ai
Проектор что это линейная алгебра
- Вы здесь:
- Главная

- Видеотека

- Естествознание

- Математика

- Высшая математика

- Линейная алгебра

- Линейная алгебра от НОУ ИНТУИТ

- Лекция 9: Проектор
Лекция 9: Проектор
Подробности Категория: Линейная алгебра от НОУ ИНТУИТ
В лекции подробно рассмотрен такой вид линейного оператора, как проектор. Рассмотрены его свойства. Разобраны задачи по указанной теме.
Источник: forkettle.ru
Вычисление проекторов матрицы
Проекторы матрицы можно также вычислить, воспользовавшись интерполяционным многочленом Лагранжа с матричным аргументом:
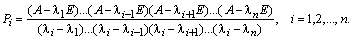
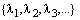
По известному спектру проекторы матрицы можно найти и методом неопределенных коэффициентов. Для чего выбирают такие функции от матрицы A, которые вычисляются очевидным образом, например, такие:
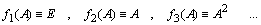
Записывая разложение для каждой функции, получим следующую систему линейных уравнений относительно проекторов:
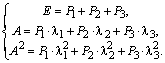
В случае, когда в спектре матрицы имеются кратные собственные значения, вычисление проекторов осуществляется по интерполяционным формулам Лагранжа, учитывающим еще и заданные значения производных в отдельных точках. Разложение матричной функции по значениям ее на спектре в этом случае имеет вид:

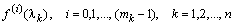
где – значения i-тых произ-водных функции в точках, соответствующих различным (не кратным) корням характеристического многочлена,
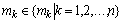 – число кратных корней
– число кратных корней 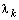 ,
,
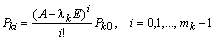
– проекторы кратных корней, в выражении которых содержатся
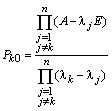
– проекторы различных корней.
9. Пример использования числовых характеристик матриц
Знание собственных значений матрицы и ее проекторов позволяет выполнять вычисления аналитических функций получающихся, например, при решениях систем линейных дифференциальных уравнений, при исследованиях эквивалентных матричных преобразований и пр.
Для примера построим матрицу с заданными собственными значениями 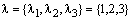 и собственными векторами, основанными на векторах
и собственными векторами, основанными на векторах 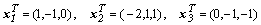 .
.
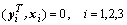
Сначала необходимо убедиться в линейной независимости исходных векторов и добиться того, чтобы левые и правые одноименные собственные векторы оказались ортогональными, т.е. . Проверка линейной независимости может быть объединена с процессом ортогонализации заданной системы векторов методом Грама-Шмидта.
Для заданных векторов построим систему векторов 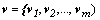 таких, что
таких, что 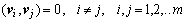 , следующим образом:
, следующим образом:
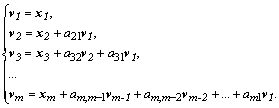
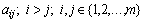
Откуда последовательно находятся коэффициенты :
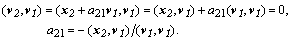
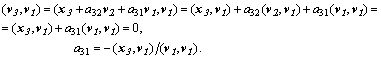
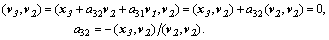
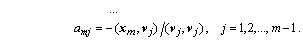
Взаимной ортогональности векторов v можно было бы добиваться и так, чтобы каждый 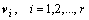 был ортогонален каждому
был ортогонален каждому 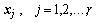 , положив
, положив 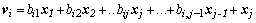 и приравняв нулю скалярные произведения
и приравняв нулю скалярные произведения 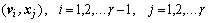 :
:
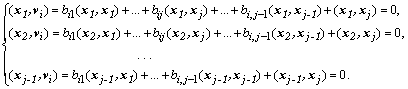
Определитель этой системы называют определителем Грама:
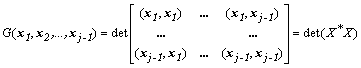
,
где — матрица, в общем случае комплексно сопряженная с матрицей
, составленной из заданных векторов.
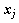
Если грамиан положителен, а он всегда неотрицателен, то векторы линейно независимы, а если равен нулю, то зависимы. Это один из способов проверки конкретного набора векторов на их линейную независимость.
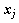
Для заданного выше набора векторов определитель произведения матрицы X на транспонированную X* будет равен
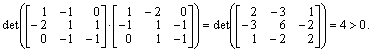
Таким образом, заданная система векторов линейно независима. Для построения ортонормированной системы векторов последовательно вычислим коэффициенты и ортогональные векторы:
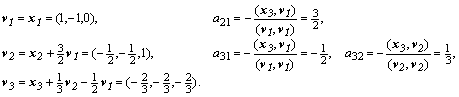
После нормирования векторы образуют правую систему собственных векторов. Транспонированная Т-матрица с этими векторами есть 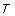 -матрица (
-матрица (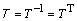 ); ее строки являются собственными левосторонними векторами:
); ее строки являются собственными левосторонними векторами:
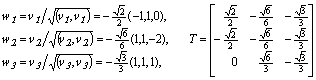
.
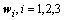
Внешнее (матричное) произведение каждого нормированного вектора самого на себя дает нам проекторы искомой матрицы:
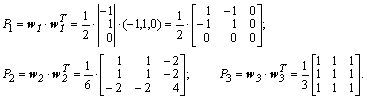
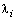
Умножая каждое собственное значение из заданного набора на свой проектор и суммируя, получим:
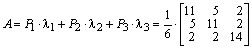
.
Аналогично получается обратная матрица:
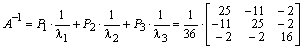
.
С помощью этих же проекторов вычисляется любая аналитическая функция, аргументом которой является матрица A:
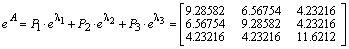
.
Информация о работе «Линейные системы уравнений»
Раздел: Математика
Количество знаков с пробелами: 21092
Количество таблиц: 0
Количество изображений: 9
Источник: kazedu.com