Для преобразования любого аналогового сигнала (звука, изображения) в цифровую форму необходимо выполнить три основные операции: дискретизацию, квантование и кодирование.
Дискретизация — представление непрерывного аналогового сигнала последовательностью его значений. Эти отсчеты берутся в моменты времени, отделенные друг от друга интервалом, который называется интервалом дискретизации. Величину, обратную интервалу между отсчетами, называют частотой дискретизации.
Понятно, что чем меньше интервал дискретизации и, соответственно, выше частота дискретизации, тем меньше различия между исходным сигналом и его дискретизированной копией. Ступенчатая структура дискретизированного сигнала может быть сглажена с помощью фильтра нижних частот. Таким образом и осуществляется восстановление аналогового сигнала из дискретизированного. Но восстановление будет точным только в том случае, если частота дискретизации по крайней мере в 2 раза превышает ширину полосы частот исходного аналогового сигнала (это условие определяется известной теоремой Котельникова). Если это условие не выполняется, то дискретизация сопровождается необратимыми искажениями.
Квантование (обработка сигнала)
Дело в том, что в результате дискретизации в частотном спектре сигнала появляются дополнительные компоненты, располагающиеся вокруг гармоник частоты дискретизации в диапазоне, равном удвоенной ширине спектра исходного аналогового сигнала. Если максимальная частота в частотном спектре аналогового сигнала превышает половину частоты дискретизации, то дополнительные компоненты попадают в полосу частот исходного аналогового сигнала. В этом случае уже нельзя восстановить исходный сигнал без искажений.
Если объект телевизионной съемки представляет собой очень быстро движущийся или, например, вращающийся предмет, то могут возникать и искажения дискретизации во временной области. Примером искажений, связанных с недостаточно высокой частотой временной дискретизации (это частота кадров телевизионного разложения), является картина быстро движущегося автомобиля с неподвижными или, например, медленно вращающимися спицами колеса (стробоскопический эффект). Если частота дискретизации установлена, то искажения дискретизации отсутствуют, когда полоса частот исходного сигнала ограничена сверху и не превышает половины частоты дискретизации.
Если потребовать, чтобы в процессе дискретизации не возникало искажений ТВ сигнала с граничной частотой, например, 6 МГц, то частота дискретизации должна быть не меньше 12 МГц. Однако, чем ближе частота дискретизации к удвоенной граничной частоте сигнала, тем труднее создать фильтр нижних частот, который используется при восстановлении, а также при предварительной фильтрации исходного аналогового сигнала.
Это объясняется тем, что при приближении частоты дискретизации к удвоенной граничной частоте дискретизируемого сигнала предъявляются все более жесткие требования к форме частотных характеристик восстанавливающих фильтров — она все точнее должна соответствовать прямоугольной характеристике. Следует подчеркнуть, что фильтр с прямоугольной характеристикой не может быть реализован физически. Такой фильтр, как показывает теория, должен вносить бесконечно большую задержку в пропускаемый сигнал. Поэтому на практике всегда существует некоторый интервал между удвоенной граничной частотой исходного сигнала и частотой дискретизации.
Оцифровка звука

Квантование — представляет собой замену величины отсчета сигнала ближайшим значением из набора фиксированных величин — уровней квантования. Другими словами, квантование — это округление величины отсчета. Уровни квантования делят весь диапазон возможного изменения значений сигнала на конечное число интервалов — шагов квантования.
Расположение уровней квантования обусловлено шкалой квантования. Используются как равномерные, так и неравномерные шкалы. Искажения сигнала, возникающие в процессе квантования, называют шумом квантования.
При инструментальной оценке шума вычисляют разность между исходным сигналом и его квантованной копией, а в качестве объективных показателей шума принимают, например, среднеквадратичное значение этой разности. В отличие от флуктуационных шумов шум квантования коррелирован с сигналом, поэтому шум квантования не может быть устранен последующей фильтрацией. Шум квантования убывает с увеличением числа уровней квантования.
Операции, связанные с преобразованием аналогового сигнала в цифровую форму (дискретизация, квантование и кодирование), выполняются одним устройством — аналого-цифровым преобразователем (АЦП). Сейчас АЦП может быть просто интегральной микросхемой.
Обратная процедура, т.е. восстановление аналогового сигнала из последовательности кодовых слов, производится в цифро-аналоговом преобразователе (ЦАП). Сейчас существуют технические возможности для реализации всех обработок сигналов звука и изображения, включая запись и излучение в эфир, в цифровой форме. Однако в качестве датчиков сигнала (например, микрофон, передающая ТВ трубка или прибор с зарядовой связью) и устройств воспроизведения звука и изображения (например, громкоговоритель, кинескоп) пока используются аналоговые устройства. Поэтому аналого — цифровые и цифро — аналоговые преобразователи являются неотъемлемой частью цифровых систем.
Сегодня обработка аналоговых сигналов с использованием цифровых преобразований все шире используется для решения множества прикладных задач в связи, радиолокации, измерительной технике, медицине и других областях науки и техники, в которых прежде доминировали аналоговые системы. Преимущества цифровых систем обусловлены рядом факторов. Прежде всего, это фактор качества получаемого или передаваемого сигнала. Аналоговые реализации зачастую не позволяют обеспечить высоких показателей качества передачи и воспроизведения сигнала, а переход на мировые стандарты ужесточает требования, предъявляемые к таким параметрам систем, как помехоустойчивость, точность, быстродействие.
31. Аналого-цифровые преобразователи. Назначение. Схемотехнические реализации, основные параметры, условные обозначения.
Аналого-цифровые преобразователи (АЦП) являются устройствами, которые принимают входные аналоговые сигналы и генерируют соответствующие им цифровые сигналы, пригодные для обработки микропроцессорами и другими цифровыми устройствами.
При преобразовании напряжения в цифровой код используются три независимых операции: дискретизация, квантование и кодирование. Процедура аналого-цифрового преобразования непрерывного сигнала представляет собой преобразование непрерывной функции напряжения u(t)в последовательность чисел u(tn),где u = 0,1,2. отнесенных к некоторым фиксированным моментам времени. При дискретизации непрерывная функция u(t)преобразуется в последовательность ее отсчетов, как показано на рис. 75, а.
Вторая операция, называемая квантованием, состоит в том, что мгновенные значения функции u(t) ограничиваются только определенными уровнями, которые называются уровнями квантования. В результате квантования непрерывная функция u(t) принимает вид ступенчатой кривой uK(t),показанной на рис. 75, б, а квантованные величины – вид цифрового кода, т. е. последовательности цифр, подчиненных определенному закону.
С помощью операции кодирования осуществляется условное представление величины напряжения.
В основе дискретизации сигналов лежит принципиальная возможность представления их в виде взвешенных сумм:
где аn– некоторые коэффициенты или отсчеты, характеризующие исходный сигнал в дискретные моменты времени, fn(t) – набор элементарных функций, используемых при восстановлении сигнала по его отсчетам.
Основные характеристики АЦП.Любой АЦП является сложным электронным устройством, которое может быть выполнено в виде одной интегральной микросхемы или содержать большое количество различных электронных компонентов. В связи с этим характеристики АЦП зависят не только от его построения, но и от характеристик элементов, которые входят в его состав. Тем не менее большинство АЦП оценивают по их основным метрологическим показателям, которые можно разделить на две группы: статические и динамические.
К статическим характеристикам АЦП относят: абсолютные значения и полярности входных сигналов, входное сопротивление, значения и полярности выходных сигналов, выходное сопротивление, значения напряжений и токов источников питания, количество двоичных или десятичных разрядов выходного кода, погрешности преобразования постоянного напряжения и др. К динамическим параметрам АЦП относят: время преобразования, максимальную частоту дискретизации, апертурное время, динамическую погрешность и др.
Рассмотрим некоторые из этих параметров более подробно. Основной характеристикой АЦП является его разрешающая способность, которую принято определять величиной, обратной максимальному числу кодовых комбинаций на выходе АЦП. Разрешающую способность можно выражать в процентах, в количестве разрядов или в относительных единицах.
Реальное значение разрешающей способности отличается от расчетного из-за погрешностей АЦП. Точность АЦП определяется значениями абсолютной погрешности, дифференциальной и интегральной нелинейности. Абсолютную погрешность АЦП определяют в конечной точке характеристики преобразования, поэтому ее обычно называют погрешностью полной шкалы и измеряют в единицах младшего разряда.
Дифференциальную нелинейность (DNL)определяют через идентичность двух соседних приращений сигнала, т. е. как разность напряжений двух соседних квантов: DNL = hi – hi+1.Определение дифференциальной нелинейности показано на рис. 76, а.
Интегральная нелинейность АЦП (INL) характеризует идентичность приращений во всем диапазоне входного сигнала. Обычно ее определяют, как показано на рис. 76, б,по максимальному отклонению сглаженной характеристики преобразования от идеальной прямой линии, т. е. INL = u’i-ui.
Время преобразования Тпробычно определяют как интервал времени от начала преобразования до появления на выходе АЦП устойчивого кода входного сигнала. Для одних типов АЦП это время постоянное и не зависит от значения входного сигнала, для других АЦП это время зависит от значения входного сигнала. Если АЦП работает без устройства выборки и хранения, то время преобразования является апертурным временем.
Максимальная частота дискретизации – его частота, с которой возможно преобразование входного сигнала, при условии, что выбранный параметр (например, абсолютная погрешность) не выходит за заданные пределы.
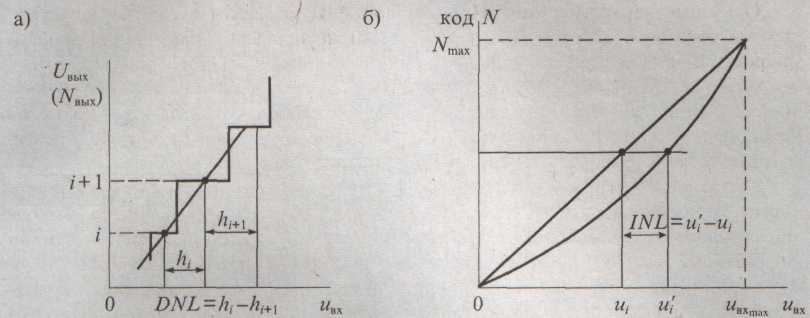
Рис. 76. Определение дифференциальной нелинейности (а)
и интегральной нелинейности (б)
Иногда максимальную частоту преобразования принимают равной обратной величине времени преобразования. Однако это пригодно не для всех типов АЦП.
Принципы построения АЦП.Все типы используемых АЦП можно разделить по признаку измеряемого значения напряжения на две группы: АЦП мгновенных значений напряжения и АЦП средних значений напряжения (интегрирующие АЦП).
АЦП мгновенных значенийможно разделить на следующие основные виды: последовательного счета, последовательного приближения, параллельные, параллельно-последовательные и с промежуточным преобразованием в интервал времени.
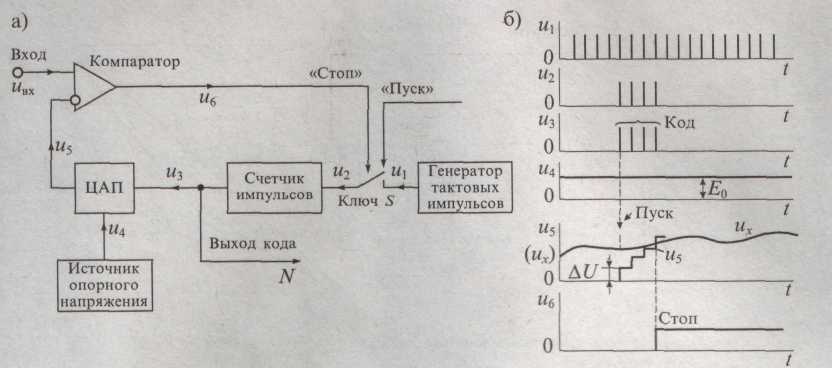
Структурная схема АЦП последовательного счета приведена на рис. 77.
АЦП обозначаются как ADC.
Источник: studopedya.ru
Кодеки телекоммукационных систем
Кодер с линейной шкалой квантования называется линейным, а с нелинейной шкалой квантования — нелинейным. Аналогичное определение относится и к декодерам. По принципам действия кодеры делятся на три основные группы: счетного типа, взвешивающего типа и матричные.
Квантование сигнала с линейной шкалой характеристики не позволяет получить высокое качество передачи сигнала с малой амплитудой. Поэтому в системах ИКМ-ВРК квантование с линейной шкалой практически не применяется. Необходимое качество передачи сигналов достигается при выполнении квантования с неравномерной шкалой. В системах ИКМ-ВРК вместо плавной амплитудной характеристики, которую имеют аналоговые компандеры, применяются сегментные характеристики. Они представляют собой кусочно-ломаную аппроксимацию плавных характеристик, при которой изменение крутизны происходит дискретными ступенями. Наибольшее распространение получила сегментная характеристика компандирования типа А-87, 6/13, где аппроксимация логарифмической характеристики производится по так называемому А-закону, соответствующему выражениям [1]:
Здесь А- коэффициент компрессии, равный 87, 6, а сама характеристика строится из 13 сегментов. Такая характеристика показана па рис. …..
Она содержит в положительной области сегменты C1, С2, Сз. C8, находящиеся между точками (узлами) 0-1, 1-2, 2-3, …, 7-8.
Аналогичным образом строится характеристика для отрицательной области значений входного сигнала. Четыре центральных сегмента (два в положительной и два в отрицательной областях) объединяются в один центральный сегмент, поэтому общее число сегментов на двухполярной характеристике равно 13. Каждый из 16 сегментов характеристики содержит по 16 шагов (уровней), квантования, а общее число уровней равно 256, из них 128 положительных и 128 отрицательных.
Каждый сегмент начинается с определенного эталона, называемого основным. Эти эталоны на рис. 53 указаны в начале каждого сегмента. Шаг квантования внутри каждого сегмента равномерный, а при переходе от одного к другому сегменту изменяется в 2 раза, начиная с центрального сегмента, куда входят С1, и С2. Значения основных и дополнительных эталонов, шагов квантования даны в таблице

Рис. 53. Характеристика компрессии типа А-87, 6/13.
Все эталонные значения в табл. 7 даны в условных единицах по отношению к значению минимального шага квантования. Сочетание дополнительных эталонов позволяет получить любой из 16 уровней квантования в данном сегменте. При изменении шага квантования изменяется крутизна характеристики. Изменение крутизны происходит в точках (узлах) характеристики.
Четыре центральных сегмента (два в положительной и два в отрицательной областях характеристики) имеют одинаковую крутизну и равные шаги квантования. При таком построении характеристики минимальный шаг квантования Δ minимеют сегменты С1 и С2 а максимальный Δ max-сегмент C8, причем отношение Δ max/ Δ minсоставляет 2 6 . или 64. Это значение примерно характеризует параметр сжатия для сегментной характеристики компандирования, или параметр А. Точное значение этого параметра для непрерывной характеристики типа А определяется из выражения:
и при числе сегментов nc= 8 значение A =87, 6.
Эффективность рассмотренной характеристики можно оценить визуально, если обратить внимание на то, что 112 уровней из 128 используются для квантования сигналов, амплитуда которых не превышает половины максимальной, 64 уровня для квантования сигналов, амплитуда которых не превышает 6, 2% максимальной.
Рассмотрим особенности этапов кодирования и декодирования сигналов при нелинейной характеристике квантования. В случае сегментной характеристики компрессии типа А-87, 6/13 для кодирования абсолютных величин отсчетов необходимо 11 эталонов с условными весами, равными 2 0 , 2 1 , 2 2 , 2 3 . 2 10 , или 1, 2, 4. 1024 уровнями квантования. При линейном кодировании такая характеристика эквивалентна характеристике квантования с 2048 уровнями. Для кодирования 2048 положительных и 2048 отрицательных уровней потребуется 12-разрядная кодовая группа. При нелинейном кодировании для обеспечения такой же защищенности Акв≥ 25 дБ потребуются 128 положительных и 128 отрицательных уровней, а кодовая группа – 8 разрядная.
Значения основных и дополнительных эталонов Таблица 7.
| Номер сегмента | Кодовая комбинация номера сегмента | Эталонные сигналы U эт | Шаг квантования | Эталонный сигнал коррекции для декодирования |
| основной | дополнительные | |||
| 1-й | 2-й | 3-й | 4-й | |
| 0, 5 | ||||
| 0, 5 | ||||
| 3 |
Кодирование осуществляется за восемь тактов и включает три основных этапа:
1 этап — определение и кодирование полярности входного сигнала;
2 этап — определение и кодирование номера сегмента узла, в котором заключен кодируемый отсчет;
3 этап — определение и кодирование номера уровня квантования сегмента, в зоне которого заключена амплитуда кодируемого отсчета.
Первый этап кодирования осуществляется за 1-й такт, второй этап — за 2. 4-й такты, третий этап — за 5. 8-й такты кодирования.

Рис. 54. Структурная схема нелинейного кодера
Кодер содержит компаратор (К), блок выбора и коммутации эталонных токов (БКЭ), генератор положительных (ГЭТ1) и отрицательных (ГЭТ2) эталонных токов, компрессирующую логику (КЛ), цифровой регистр (ЦР) и преобразователь кода (ПК).
Компаратор определяет знак разности между амплитудами токов кодируемого отсчета Iс и эталона Iэт. Если амплитуда тока кодируемого отсчета Iс > тока эталона Iэт, то на выходе компаратора формируется 0, а если амплитуда тока кодируемого отсчета Iс < тока эталона Iэт — то на выходе компаратора будет сформирована 1. В зависимости от решений компаратора ЦР выбирает полярность ГЭТ и управляет работой компрессирующей логики. Кроме того, цифровой регистр, служит для записи решений компаратора после каждого такта кодирования и формирования структуры кодовой группы.
Генератор эталонов формирует полярность и величины эталонов. По построению он аналогичен ГЭТ линейного кодера, только количество формируемых эталонов равно 11, а значения этих эталонов равны 1, 2, 4. 1024 уровней квантования.
По мере образования кодовой комбинации формирователь считывает состояние выходов 1, 2. 8 ЦР, преобразуя параллельный код в последовательный. Работой узлов кодера управляют устройства генераторного оборудования системы передачи.
Рассмотрим принцип работы нелинейного кодера на примере отсчета, амплитуда которого равна — 236 у.е.
В исходном состоянии все ключи разомкнуты, все разряды ЦР и ПК обнулены.
1-й этап кодирования. Кодирование полярности отсчета АИМ-сигнала.
Выбор ГЭС-1 илиГЭС-2.
1-й разряд. По 1-му проводу от распределителя разрядного РР ГОпер. поступает импульс в 1-ю ячейку цифрового регистра ЦР. Этот импульс через БКЭ проходит в ГЭС-1, в котором находится эталонный сигнал 0 у.е. Этот эталонный сигнал используется для определения полярности отсчета. Замыкается ключ, подключающий ГЭС-1.
Эталонный сигнал 0 у.е. поступает в КОМПАРАТОР, где сравнивается с амплитудой отсчета.
Так как эталонный ток 0 у.е. больше, чем — 236, то на выходе компаратора формируется импульс, который по цепи обратной связи поступает в Цифровой регистр и стирает импульс из его 1-й ячейки. Эталонный сигнал 0 у.е. отключается, ключ, подключивший ГЭС-1, размыкается. Замыкается ключ, подключающий ГЭС-2 на оставшиеся 7 разрядов кодирования.
1-й этап завершился выбором ГЭС-2.
2-й этап кодирования. Выбор основного эталонного сигнала U осн.эт.
2-й разряд. По 2-му проводу от РР ГО пер. поступает импульс во 2-ю ячейку Цифрового регистра. Компрессирующая логика КЛ считывает комбинацию, записанную в 2, 3 и 4-м разрядах ЦР (100) и через БКЭ дает команду в ГЭС-2 замкнуть ключ 1-го основного эталонного сигнала Uосн.эт. = 128 у.е.
Эталонный сигнал 128 у.е. поступает в компаратор, сравнивается с амплитудой отсчета 236 у.е. Так как эталонный сигнал 128 у.е. меньше амплитуды отсчета, то на его выходе пробел (0), и импульс во 2-й ячейке цифрового регистра сохраняется. Эталонный сигнал 128 у.е. отключается.
3-й разряд. По 3-му проводу от РР ГО пер. поступает импульс в 3-ю ячейку Цифрового регистра. Компрессирующая логика КЛ считывает комбинацию, записанную в 2, 3 и 4-м разрядах ЦР (110) и через БКЭ дает команду в ГЭС-2 замкнуть ключ основного эталонного сигнала 512 у.е.
Эталонный сигнал 512 у.е. поступает в компаратор, сравнивается с амплитудой отсчета 236 у.е. Так как эталонный сигнал 512 у.е. больше амплитуды отсчета, то на выходе компаратора формируется импульс, который по цепи обратной связи поступает в цифровой регистр и стирает импульс в 3-й ячейке цифрового регистра. Эталонный сигнал 512 у.е. отключается.
4-й разряд. По 4-му проводу от РР ГО пер. поступает импульс в 4-ю ячейку Цифрового регистра. Компрессирующая логика КЛ считывает комбинацию, записанную в 2, 3 и 4-м разрядах ЦР (101) и через БКЭ дает команду в ГЭС-2 замкнуть ключ основного эталонного сигнала 256 у.е.
Эталонный сигнал 256 у.е. поступает в компаратор, сравнивается с амплитудой отсчета 236 у.е. Так как эталонный сигнал 256 у.е. меньше амплитуды отсчета, то на выходе компаратора – пробел (0) и импульс в 4-й ячейке цифрового регистра сохраняется.
Во 2, 3 и 4-м разрядах сформировалась комбинация 100. Поэтому КЛ выбирает основной эталонный сигнал 256 у.е. и, замкнув ключ этого основного эталонного сигнала, подключает этот основной эталонный сигнал 256 у.е. к компаратору на оставшиеся четыре разряда.
3-й этап кодирования. Выбор дополнительных эталонных сигналов Uдоп.эт.
5-й разряд. По 5-му проводу от РР ГО пер. поступает импульс в 5-ю ячейку Цифрового регистра. КЛ через БКЭ дает команду в ГЭС-2 замкнуть ключ 1-го дополнительного эталонного сигнала 64 у.е, который поступает в компаратор и сравнивается с амплитудой отсчета 236 у.е.
Так как сумма эталонных сигналов (128 + 64 = 192 ) меньше амплитуды отсчета 236, то на выходе компаратора пробел и импульс в 5-й ячейке ЦР сохраняется. Ключ 1-го дополнительного эталонного сигнал 64 у.е. в ГЭС-2 остается замкнутым, и этот эталонный сигнал в компараторе сохраняется.
6-й разряд. По 6-му проводу от РР ГО пер. поступает импульс в 6-ю
ячейку Цифрового регистра. КЛ через БКЭ дает команду в ГЭС-2 замкнуть ключ 2-го дополнительного эталонного сигнала 32 у.е, который поступает в компаратор и сравнивается с амплитудой отсчета 236 у.е. Так как сумма эталонных сигналов (128 + 64 + 32 = 224) меньше амплитуды отсчета 236, то на выходе компаратора формируется 0, который по цепи обратной связи поступает в Цифровой регистр и сохраняет импульс в 6-й ячейке ЦР.
Ключ эталонного сигнала 32 у.е. в ГЭС-2 остается замкнутым и этот эталонный сигнал в компараторе сохраняется.
7-й разряд. По 7-му проводу от РР ГО пер. поступает импульс в 7-ю ячейку Цифрового регистра. КЛ через БКЭ дает команду в ГЭС-2 замкнуть ключ 3-го дополнительного эталонного сигнала 16 у.е, который поступает в компаратор и сравнивается с амплитудой отсчета 236.
Так как сумма эталонных сигналов (128 + 64+ 32+16 = 2 48) больше амплитуды отсчета 236, то на выходе компаратора импульс, который по цепи обратной связи поступает в Цифровой регистр и стирает импульс в 7-й ячейке ЦР. Ключ 3-го дополнительного эталонного сигнала 16 у.е. в ГЭС-2 размыкается и этот эталонный сигнал из компаратора удаляется.
8-й разряд. По 8-му проводу от РР ГО пер. поступает импульс в 8-ю ячейку Цифрового регистра. КЛ через БКЭ дает команду в ГЭС-2 замкнуть ключ 4-го дополнительного эталонного сигнала 8 у.е, который поступает в компаратор и сравнивается с амплитудой отсчета 236 у.е.
Так как сумма эталонных сигналов (128 + 64 + 32+ 8 = 232) меньше амплитуды отсчета 236, то на выходе компаратора пробел. Импульс в 7-й ячейке ЦР сохраняется. Ключ 4-го дополнительного эталонного сигнал 8 у.е. в ГЭС-2 остается замкнутым, и этот эталонный сигнал в компараторе сохраняется.
В 8-ми разрядах Цифрового регистра сформировалась кодовая комбинация 01001101.
Абсолютная величина ошибки квантования рассчитывается по формуле
ξ кв.абс. = Uаим -∑ Uэт = 236 — (128 + 64 + 32 +8) = 236- 232 = 4 у.е.
Ошибка квантования ξ кв.абс. сравнивается с шагом квантования Δ и рассчитывается ее относительная величина в %. Для закодированного отсчета — 236у.е
ξ кв. отн. = (4 у.е: 8 ) х 100% = 50 %.
СОДЕРЖАНИЕ
Источник: studopedia.info
Критерии точности представления квантованного сигнала

Наиболее простыми и часто используемыми видами квантования являются:
· квантование по уровню (будем говорить просто квантование);
· квантование по времени (будем называть дискретизацией);
Ниже приведены варианты графического представления (рис. 2.1, 2.2, 2.3) этих видов квантования.
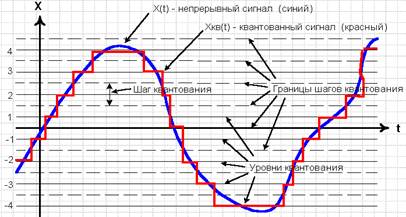
Рис. 2.1. Квантование по уровню (квантование).
Совокупность уровней и границ квантования называют шкалой квантования.
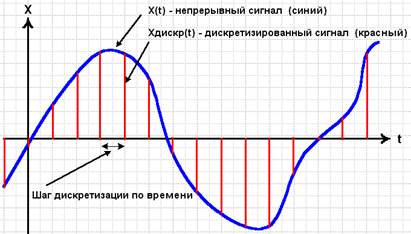
Рис. 2.2. Дискретизация по времени (дискретизация).
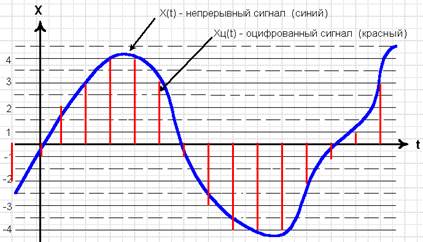
Рис. 2.3. Квантование и по уровню и по времени.
Формы квантования только по уровню или только по времени являются непрерывно-дискретными, т.к. в первом случае непрерывной величиной является время ti перехода с одного уровня на другой, а во втором – значение x(ti) квантуемой величины в дискретный момент времени ti.
При квантовании же по уровню и по времени одновременно и время и уровень принимают конечное количество значений, что с технической точки зрения выгоднее всего. Точность представления сигнала, однако, в этом случае наименьшая.
Кроме трех вышеупомянутых видов квантования существует и все шире используется четвертый вид – представление сигнала путем разложения его в ряд по некоторой системе функций: , где − система функций, по которым выполняется разложение сигнала, а − коэффициенты разложения. Ниже показывается, что коэффициенты разложения Сk являются непрерывными величинами. Поэтому здесь мы по сути дела имеем дело с непрерывно-дискретной формой представления сигнала. Для перехода к полностью дискретной форме эти коэффициенты нужно проквантовать по уровню.
Исследуем точность представления квантованного сигнала. Для этого прежде всего нужно определить критерии точности.
Критерии точности представления квантованного сигнала
В результате обратного преобразования из непрерывно-дискретной формы в непрерывную получается сигнал , отличающийся от исходного на величину ошибки . Сигнал называется воспроизводящей функцией.
Способы дискретизации и воспроизведения влияют на ошибку и ее параметры. Обычно, чем шире шаг квантования по уровню или по времени или чем меньше количество n членов разложения сигнала в ряд, тем больше ошибка и одновременно меньше данных нужно передавать через канал связи или меньше объем памяти, требуемый для хранения этого сигнала. Поэтому, зная связь между параметрами дискретизации и восстановления, надо выбирать компромиссное решение, удовлетворяющее как по точности, так и по объемам данных.
Ошибка является функцией времени и потому неудобна для использования в качестве критерия точности тракта дискретизация-восстановление.
Поэтому в качестве такого критерия обычно используют какой-либо функционал ошибки.
1. Чаще всего в качестве такого функционала применяют среднеквадратическую погрешность, определяемую по формуле:
Здесь Т – некоторый временной интервал, на котором находится среднеквадратическая ошибка.
2. Иногда применяют другой критерий – наибольшее отклонение:
Однако его использование затруднено из-за необходимости априорного знания максимального значения сигнала и его производных.
3. Еще один критерий называется интегральным. Он находится по формуле: .
Интегральный критерий характеризует в основном отклонение среднего значения воспроизведенного сигнала от исходного. Его имеет смысл использовать тогда, когда целью передачи сигнала является передача именно его среднего значения. Критерий характеризуется минимальными объемами требуемых априорных знаний о передаваемом сигнале.
Вероятностный критерий задается формулой: , где − ширина доверительного интервала, а − доверительная вероятность.
Вероятностныйкритерий показывает с какой вероятностью отклонения воспроизведенного сигнала от исходного не выйдет за пределы доверительного интервала. Очевидно, что, чем ширина интервала меньше, а вероятность выше, тем точность воспроизведения сигнала будет больше. Однако отсутствие больших отклонений от исходного сигнала при этом не гарантируется.
Информационныйкритерий. При использовании этого критерия рассматривается количество информации, заключенной в воспроизведенном сигнале относительно исходного.
3. Формулировка теоремы Найквиста-Котельникова и ее ограничения.
Котельников доказал, что, если некоторый сигнал x(t) имеет ограниченный сверху частотой fm спектр, то его можно проквантовать по времени с периодом и затем с абсолютной точность восстановить по формуле:
Ряд (2.6) называется рядом Котельникова, а вышеуказанное утверждение – теоремой Котельникова.
По определению сигнал x(t) и его спектр S(jω) находятся в следующих отношениях:
Формулы (2.7) и (2.8) образуют пару преобразований Фурье (прямое и обратное. Ограниченный интервал интегрирования в (2.8) – следствие ограниченности спектра, поскольку . Здесь ω – круговая частота, а .
Полиномы Лагранжа и их использование для восстановления непрерывных сигналов,
Воспроизводящая функция в большинстве случаев рассчитывается по формуле: , где − некоторые функции. Эти функции обычно стремятся выбрать так, чтобы
В этом случае , т.е. значения воспроизводящей и исходной функций совпадают в моменты взятия отсчетов или, как принято говорить, в узлах интерполяции.
Функции, обладающие этим качеством, нашел выдающийся французский математик и механик Жозеф Луи Лагранж (1736-1813).
Функции Лагранжа L зависят от одного аргумента t и двух параметров – n и k. Здесь n – максимальный номер отсчета, а k – номер функции.
Несложно доказать, что функции Лагранжа отвечают условию (2.14). Из формулы (2.15) следует, что функция Лагранжа является полиномом n-ой степени. Воспроизводящая функция по этой причине также является полиномом и называется полиномом Лагранжа n-ой степени.
Полином Лагранжа можно использовать для расчета воспроизводящей функции как при равномерной, так и при неравномерной дискретизации. Если же ограничиться только равномерной дискретизацией, полином Лагранжа можно преобразовать к виду:
Источник: megaobuchalka.ru