Вопрос по физике:
В процессе броуновского движения небольшие твёрдые частицы в жидкостях:
1) медленно оседают вниз под действием силы тяжести
2) поднимаются вверх против направления действия силы тяжести
3) беспорядочно совершают небольшие перемещения под действием конвекционных потоков жидкости
4) совершают беспорядочные перемещения под действием ударов молекул жидкости
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
- bookmark_border
- 21.03.2016 06:02
- Физика
- remove_red_eye 7153
- thumb_up 26
Источник: online-otvet.ru
7 класс
Глава 3. Давление твёрдых тел. жидкостей и газов
§ 52. Плавание тел
На тело, находящееся внутри жидкости, действуют две силы: сила тяжести, направленная вертикально вниз, и архимедова сила, направленная вертикально вверх.
Центробежная сила
Рассмотрим, что будет происходить с телом под действием этих сил, если вначале оно было неподвижно.
При этом возможны три случая:
1) если сила тяжести Fтяж больше архимедовой силы FA, то тело будет опускаться на дно, тонуть, т. е. если
Fтяж > FA, то тело тонет;
2) если сила тяжести Fтяж равна архимедовой силе FA, то тело может находиться в равновесии в любом месте жидкости, т. е. если
Fтяж = FA, то тело плавает;
3) если сила тяжести Fтяж меньше архимедовой силы FA, то тело будет подниматься из жидкости, всплывать, т. е. если
Fтяж < FA, то тело всплывает.
Рассмотрим последний случай подробнее.
Когда всплывающее тело достигнет поверхности жидкости, то при дальнейшем его движении вверх архимедова сила будет уменьшаться. Почему? Да потому, что будет уменьшаться объём части тела, погружённой в жидкость, а архимедова сила равна весу жидкости в объёме погружённой в неё части тела.
Когда архимедова сила станет равной силе тяжести, тело остановится и будет плавать на поверхности жидкости, частично погрузившись в неё.
Полученный вывод легко проверить на опыте.
В отливной сосуд наливают воду до уровня боковой трубки. После этого в сосуд погружают плавающее тело (рис. 153), предварительно взвесив его в воздухе. Опустившись в воду, тело вытесняет объём воды, равный объёму погружённой в неё части тела. Взвесив эту воду, находят, что её вес (архимедова сила) равен силе тяжести, действующей на плавающее тело, или весу этого тела в воздухе.

Рис. 153. Вытеснение воды телом
Проделав такие же опыты с любыми другими телами, плавающими в разных жидкостях — в воде, спирте, растворе соли, можно убедиться, что если тело плавает в жидкости, то вес вытесненной им жидкости равен весу этого тела в воздухе.
Физика 7 класс (Урок№12 — Сила. Сила тяжести.)
Легко доказать, что если плотность сплошного твёрдого тела больше плотности жидкости, то тело в такой жидкости тонет. Тело с меньшей плотностью всплывает в этой жидкости. Кусок железа, например, тонет в воде, но всплывает в ртути. Тело же, плотность которого равна плотности жидкости, остаётся в равновесии внутри жидкости.
Плавает на поверхности воды и лёд (рис. 154), так как его плотность меньше плотности воды.

Рис. 154. Плавание тел
Чем меньше плотность тела по сравнению с плотностью жидкости, тем меньшая часть тела погружена в жидкость (рис. 155).

Рис. 155. Погружение в жидкость тел различной плотности
При равных плотностях твёрдого тела и жидкости тело плавает внутри жидкости на любой глубине.
Две несмешивающиеся жидкости, например вода и керосин, располагаются в сосуде в соответствии со своими плотностями: в нижней части сосуда — более плотная вода (ρ = 1000 кг/м 3 ), сверху — более лёгкий керосин (ρ = 800 кг/м 3 ).
Средняя плотность живых организмов, населяющих водную среду, мало отличается от плотности воды, поэтому их вес почти полностью уравновешивается архимедовой силой. Благодаря этому водные животные не нуждаются в столь прочных и массивных скелетах, как наземные. По этой же причине эластичны стволы водных растений.
Плавательный пузырь рыбы устроен так, что легко меняет свой объём. Когда рыба с помощью мышц опускается на большую глубину и давление воды на неё увеличивается, пузырь сжимается, объём тела рыбы уменьшается и она не выталкивается вверх, а плавает в глубине. При подъёме объём плавательного пузыря и, соответственно, объём всего тела рыбы увеличивается, и она плавает уже на меньшей глубине. Таким образом рыба может в определённых пределах регулировать глубину своего погружения.

Плавание рыб на больших глубинах
Морские млекопитающие киты регулируют глубину своего погружения за счёт уменьшения и увеличения объёма лёгких.
Вопросы:
1. При каком условии тело, находящееся в жидкости, тонет; плавает? всплывает?
2. Как показать на опыте, что вес жидкости, вытесненной плавающим телом, равен весу тела в воздухе?
3. Чему равна выталкивающая сила, которая действует на тело, плавающее на поверхности жидкости?
4. Как зависит глубина погружения в жидкость плавающего тела от его плотности?
5. Почему водные животные не нуждаются в прочных скелетах?
6. Какую роль играет плавательный пузырь у рыб?
7. Как регулируют глубину погружения киты?
Упражнения:
Упражнение № 2
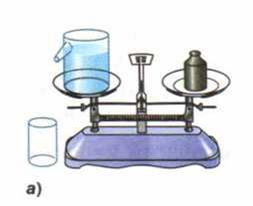
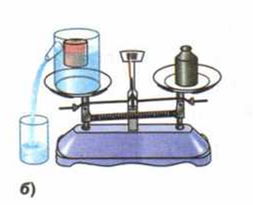
1. На весах уравновесили отливной сосуд с водой (рис. 156, а). В воду опустили деревянный брусок. Равновесие весов сначала нарушилось (рис. 156, б). Ho когда вся вода, вытесненная плавающим бруском, вытекла из сосуда, равновесие весов восстановилось (рис.
156, в). Объясните это явление.

2. На рисунке 157 изображено одно и то же тело, плавающее в двух разных жидкостях. Плотность какой жидкости больше? Почему? Что можно сказать о силе тяжести, действующей на тело, и архимедовой силе в том и другом случае?

3. Яйцо тонет в пресной воде, но плавает в солёной. Объясните почему. Пронаблюдайте это сами на опыте.
4. Изобразите графически силы, действующие на тело, плавающее на воде, всплывающее на поверхность воды, тонущее в воде.
5. Пользуясь таблицами плотности 2—4, определите, тела из каких металлов будут плавать в ртути, а какие — тонуть.
6. Будет ли кусок льда плавать в бензине, керосине, глицерине?
Задания:
1. Французский учёный Декарт (1596—1650) для демонстрации некоторых гидростатических явлений придумал прибор.
Высокий стеклянный сосуд (банку) наполняли водой, оставляя сверху сосуда небольшой объём воздуха. В этот сосуд опускали небольшую полую стеклянную фигурку. Фигурку заполняли частично водой и частично воздухом так, чтобы она только немного выходила из воды. Сверху стеклянный сосуд плотно закрывали куском тонкой кожи. Нажимая на кожу, можно было заставить фигурку плавать в воде и на воде, а также тонуть.
2. Изготовьте такой прибор («картезианский водолаз») и проделайте с ним опыты. Фигурку замените небольшим поплавком, а сосуд закройте резиновой плёнкой (рис. 158, а. На рисунке 158, б изображён другой вариант этого прибора).

3. Объясните действие прибора. Продемонстрируйте на этом приборе законы плавания тел.
Источник: xn—-7sbbfb7a7aej.xn--p1ai
Тонкая взвесь капель или тв частиц в воздухе не оседает под действием силы тяжести

Как облака наполняются водой

2015-03-25
Строго говоря, облака не заполнены водой. Он не губки, которые впитывают воду. Облака состоит из очень мелких жидких капель или кристалликов льда, взвешенных в воздухе. Капли воды и кристаллы льда, можно сравнить с поплавком, так как они настолько малы, что сопротивление воздуха уравновешивается гравитацией.
Чтобы быть более точным, капли воды и кристаллы льда, на самом деле не плавают неподвижно в небе. Они постоянно очень медленно падают под действием силы тяжести и иногда поднимаются в восходящем потоке воздуха. Это падение настолько медленно, а облака являются настолько большими и далекими, что трудно для случайного наблюдателя на земле, заметить это движение.
В книге «Физика облаков» Louis J. Battan, приведены следующие цифры: капля радиусом 10 мкм падает со скоростью 1 см / сек, капля радиуса 50 мкм уже падает со скоростью 26 см / сек. В случае, когда происходит увеличение капель в размере в результате столкновения и слияний, капли могут получаться настолько большими, что сопротивление воздуха не играет большой роли (при радиусе > 0,1 мм). Такие капли падают в виде дождя.
Облака в основном состоят из воздуха. Когда мы говорим, ведро наполнено водой, мы имеем в виду, что почти все свободное пространство, в ведре содержит воду. В облаке, все не так. Вода, составляющие облако падает в виде дождя задолго до того, когда оно сольется достаточно, чтобы заполнить весь объем облака. Удивительно, но только одна миллиардная часть объема облака состоит из воды.
Все остальное — воздуха.
Как же облака могут быть так визуально яркими, если они состоят почти их воздуха? Главная причина в отражении света от поверхности объектов. Чем больше площадь поверхности, тем больше света отражается. Облака же кажутся белыми по тому же, почему снег выглядит белым. Так что, хотя облако не содержит много воды, с точки зрения общего объема, но триллионы маленьких капелек, в сумме обеспечивают многократное отражение и преломление.
Приведем пример в цифрах, предположим, что облако состоит из капель воды, которые все имеют радиус $R$ и равномерно распределены. Предположим, общий объем облака постоянен и равен $V$, а общий объем воды в этом облаке — $V_$. Объем единичной сферической капли воды $frac pi r^$, количество капель $N$, то есть полный объем воды в облаке: $V_ = N frac pi r^$.
Кроме того, площадь поверхности одной сферы $4 pi r^$, так что общая площадь поверхности капель по всей облака $S_> = N 4 pi r^$. Решаем полученную систему получаем: $ S_> = frac<3V_>$. Так как общий объем воды фиксирован, это уравнение говорит нам, что если радиус каждой капли уменьшается, общая площадь капель поверхности будет увеличиваться. Для облака капель с очень маленьким размером, общая площадь поверхности облака будет очень высокой. Так как количество света, отраженного от объекта сильно зависит от площади поверхности, отражательная способность такого облака будет очень высокой, несмотря на то, что это по сути воздух.
Следует отметить, что, хотя отдельные капли уменьшаются в размерах, их индивидуальная площадь поверхности, конечно, становится меньше. Но при фиксированном общем объеме воды в облаке, общее количество капель меньшего размера будет больше, что означает большую общую площадь поверхности.
Источник: earthz.ru