Геометрия… Страшное слово для бесчисленного множества учеников. Они знают свойства фигур и выучили определения и теоремы, но задачи по геометрии все равно остаются какой-то китайской грамотой.
Это про тебя? Тогда ты попал туда, куда нужно!
Проблема подавляющего большинства учеников в том, что они не умеют обдумывать задачу по геометрии. Их этому не научили (ну, или они не захотели научиться, когда была возможность). Именно в этой статье, я объясню саму технологию обдумывания и, в конечном счете, нахождения решения ПРАКТИЧЕСКИ ЛЮБОЙ задачи по геометрии.
Сразу оговорюсь — без знания теории в геометрии никак. В смысле, вообще никак, от слова «совсем». Чтоб тебе было полегче при чтении этой статьи, я буду внутри решений задач в скобках курсивом указывать используемые свойства и теоремы. Но помни: если вдруг в знании теории у тебя пробел – закрытие его за тобой! Бери учебник и читай. Причем главные вещи – заучивай (или понимай).
Знать теорию – обязательно!
Ты играл когда-нибудь в квесты? Неважно в реальной жизни или в компьютере. Во всех квестах принцип один – у тебя есть что-то (вещи, знания, навыки) и есть цель (раскрыть какую-нибудь тайну, найти некий предмет, «спасти принцессу» и т.д.). При этом путь к цели – неизвестен. И зачем нужны эти самые имеющиеся у тебя «вещи, знания, навыки» – тоже непонятно. Что делать?
Очень красивое, простое и быстрое решение задачи по геометрии с экзамена
Как достичь цели?
Известно как: использовать то, что есть, и искать, куда это применить, чтоб продвинуться к цели. То есть, делать шаги от своего текущего местонахождения – к цели. При этом понятно, что некоторые шаги будут вести нас не туда, куда надо, а совсем даже в тупик. А иногда мы будем находить вещи или информацию, вроде бы напрямую к цели не ведущие, но как выяснится в дальнейшем – необходимую.
Более того, порой можно логически двигаться и наоборот – от цели к твоей текущей позиции. Например, если нужно «спасти принцессу из замка», то понятно, что, скорее всего, надо будет как-то попасть в замок. А для этого надо оказаться на острове, где этот замок стоит. Как попасть? Может быть на лодке. Или найти телепорт.
Или использовать магию. Но на остров – надо. Начинаем искать пути на остров. Это уже логические шаги от цели к текущей позиции.
К чему весь этот разговор? Решение задачи по геометрии это точно такой же «квест», только математический . Вдумайся: у нас всегда есть некоторые исходные данные и есть то, что нужно найти (или доказать – разницы на самом деле практически нет). И наша задача – построить логическую цепочку от исходных данных к цели. Строительным материалом при этом у нас будут данные (исходные и полученные при рассуждениях), а также теоремы и свойства.
Ладно, давай уже конкретный пример разберем.
Задача. В треугольнике (ABC) из точки (B) проведена высота (BH). Найти длину отрезка (AH), если известно, что сторона (AC; =; 14) см и угол (A) равен углу (C).
Так. С чего начинается решение геометрической задачи? Ну, а с чего начинается решение квеста? Правильно, осматриваемся по сторонам, изучаем, что у нас есть и куда нас жизнь закинула.
КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | Математика
В геометрии это означает:
- построить чертежа выделить из условия задачи исходные данные, то есть, выяснить, что нам дано.
- выделить из условия задачи исходные данные, то есть, выяснить, что нам дано.

Хорошо. Значит, текущая ситуация у нас такова:

Давайте потихоньку развеивать туман. Нам известно, что углы (А) и (С) равны, а это значит, что треугольник (АВС) – равнобедренный с основанием АС (теория – «признак равнобедренного треугольника: равенство углов при одной из сторон. Она и является основанием»). Это новая информация, новые данные, изначально неизвестные. Делаем шаг.

Отлично. Теперь смотрим, что у нас есть еще? Еще у нас есть информация, что (BH) – высота. А раз треугольник (ABC) – равнобедренный, то значит (BH) еще и медиана (теорема о высоте в равнобедренном треугольнике: высота, проведенная к основанию равнобедренного треугольника является медианой и биссектрисой). То есть, мы, используя новые, полученные на предыдущем шаге данные, а также исходные данные и знание теории, делаем еще один шаг и опять получаем новую информацию.

А что мы знаем про медиану? Она делит противоположную сторону на две равные части (определение медианы: отрезок, соединяющий вершину треугольника с серединой противоположной стороны). Но тогда получается, что точка (H) делит сторону (AC) пополам. То есть (AH = HC).
Стоп. Так у нас же есть длина стороны (AC)! И если мы знаем, что точка (H) делит сторону (AC) пополам, значит, (AH) равен половине (AC)! Таким образом, получаем, что (AH = AC/2 = 14/2=7) см.

Готово. Ответ получен.
Естественно, такие конструкции с «пятном тумана» рисовать каждый раз не нужно, эта схема показывает логическую цепочку решения у нас в голове. А записывается примерно так:
Источник: cos-cos.ru
ОГЭ, Математика.
Геометрия: Задача №FE8B32

Проектор полностью освещает экран A высотой 50 см, расположенный на расстоянии 140 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 260 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Решение задачи:
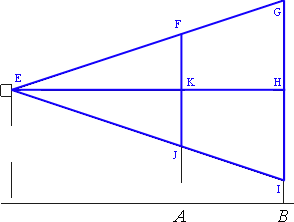
Обозначим треугольники и их ключевые точки как показано на рисунке.
Рассмотрим треугольники EGI и EFJ.
Прямая EH перпендикулярна обоим экранам и проходит через их центр, следовательно является серединным перпендикуляром.
То есть, FK=FJ/2=50/2=25 и GH=GI/2=260/2=130.
Рассмотрим треугольники EFK и EGH.
∠FEK — общий для обоих треугольников.
∠EKF=∠EHG=90° (т.к. EH — серединный перпендикуляр).
Тогда, по первому признаку подобия, данные треугольники подобны.
Следовательно, мы можем записать пропорцию сторон:
EH/EK=GH/FK
EH/140=130/25
EH=(130*140)/25=728
Ответ: 728
Источник: otvet-gotov.ru
Г) Решение практико-ориентированных задач.
Тип урока: урок обобщения и систематизации знаний.
Оборудование: мультимедийный проектор, презентация, раздаточный материал.
Форма проведения урока: беседа, индивидуальная работа, работа в микрогруппах.
План урока
1. Организационный момент – 1 мин;
2. Объявление темы и постановка целей урока — 2 мин;
3. Повторение, обобщение и систематизация учебного материала:
а) Разминка (ребусы, фронтальный опрос) – 3 мин;
б) Теория (призма, пирамида, конус, цилиндр, сфера, шар) – 5 мин;
в) Математический диктант «Верно или неверно?» — 5 мин;
г) Решение практико-ориентированных задач – 10 мин;
д)Многогранники и тела вращения в жизни – 10 мин. (заслушиваются подготовленные сообщения);
4. Подведение итогов урока. Рефлексия – 3 мин;
5. Домашнее задание – 1 мин.
Ход урока
Организационный момент.
Я приветствую Вас на уроке математики. Сегодня мне хочется, чтобы вы ещё раз убедились, что математика интересная и увлекательная наука, тесно связанная с жизнью и окружающим миром.
Объявление темы и постановка целей урока.
Тема нашего урока: «Объемы многогранников и тел вращений».
Цель урока: повторить виды многогранников и тел вращений, их элементы и формулы объемов; совершенствовать умения обучающихся применять накопленные знания в изменяемой ситуации, делать выводы и обобщения; показать практическую значимость данной темы в жизни человека.
Сегодняшнее занятие будет проходить по следующему алгоритму: мы класс разделим на пять микрогрупп. Каждая подгруппа выбирает командира. Он будет оценивать работу каждого в микрогруппе, используя оценочный лист (табл. 1).
Таблица 1 – Оценочный лист
| Ф.И. | Разминка | Теория | Мат-кий диктант | Решение задач | Многогранники и тела вращения | Итого |
0–14 баллов — удовлетворительно; 15–24 баллов — хорошо; 25–31 баллов — отлично.
Пожелаем друг другу успехов и начнём работу.
Повторение, обобщение и систематизация учебного материала.
А) Разминка (до 3 баллов).
Ребята, давайте начнём наш урок с умственной разминки. Внимание на доску. Перед вами три ребуса (рис. 1). Разгадав ребусы, вы узнаете, о чем пойдет речь на нашем уроке.
Рисунок 1 – Ребусы
О чем же пойдет речь на нашем уроке? (о многогранниках).
Что называется многогранником? (многогранник — это геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, называемыми гранями).
Какие многогранники знаете? (пирамида, параллелепипед, куб, призма, тетраэдр, икосаэдр, октаэдр, додекаэдр).
Перед вами следующие три ребуса (рис. 2).

Рисунок 2 – Ребусы
Разгадав ребусы, вы назвали тела вращения, которые мы изучали на уроках геометрии.
Почему их называют телами вращения? (Тела вращения — объёмные тела, возникающие при вращении плоской фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости).
Следующий ребус (рис. 3):

Рисунок 3 – Ребус
Разгадав ребус, мы определили тему нашего урока «Объемы многогранников и тел вращений». Трудно назвать чаще встречающиеся задачи на практике, чем задачи на вычисление объёмов. Прежде чем приступить к решению задач, давайте вспомним необходимый теоретический материал.
Б) Теория (до 5 баллов).
Вашим домашним заданием было повторить теоретический материал о многогранниках и телах вращения.
Задание: каждая микрогруппа расскажет о модели (определение, свойства, формулы и т. д.), другие могут дополнять. Фигуру для микрогруппы выбирает учитель.
Спасибо за ваше ответственное отношение к подготовке домашнего задания. Командиры, не забудьте оценить работу микрогруппы.
Теперь, повторив теорию, вы готовы к выполнению математического диктанта «Верно или неверно?».
в) Математический диктант «Верно или неверно?» (каждый верный ответ 1 балл) Презентация.
Задание: перед вами вопросы, ответьте на них с помощью знаков « +» и «−». На выполнение задания 5 минут.
1) Объем любого многогранника можно вычислить по формуле:
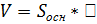
.
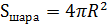
2) Неверно, что

3) Верно ли, что если объем куба равен 64 , то сторона равна 8 см.?

4) Верно ли, что если сторона куба равна 5 см, то объём равен 125 .
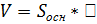
5) Верно ли, что объем конуса и пирамиды можно вычислить по формуле: .
6) Неверно, что высота прямой призмы равна ее боковому ребру.
7) Верно ли, что все грани правильной пирамиды равносторонние треугольники?
8) Верно ли, что если в прямоугольный параллелепипед вписан шар, то параллелепипед – куб?
9) Верно ли, что образующая цилиндра больше его высоты?
10) Верно ли, что ли осевое сечение цилиндра может быть трапецией?
11) Верно ли, что объём цилиндра меньше объёма любой описанной около него призмы?
12) Верно ли, что если осевые сечения двух цилиндров – равные прямоугольники, то объёмы цилиндров тоже равны?
13) Неверно, что осевое сечение цилиндра — квадрат.
14) Верно ли, что многогранник называют правильным, если в основании лежит правильный многоугольник.
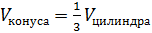
15) Верно ли, что если в цилиндр вписан конус, то ?
Внимание на экран. Правильные ответы (табл. 2):
Таблица 2 — Ответы на математический диктант.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| — | — | — | + | + | — | — | + | + | — | — | — | + | + | — |
Проверьте ваши ответы. Передайте бланки командирам на проверку и для заполнения оценочного листа.