Молекулы всех газов при одной и той же температуре обладают одинаковой средней кинетической энергией. Причем давление газа при данной температуре зависит только от числа молекул в единице объема газа. В основе объяснений физических свойств газов и законов газового состояния лежит кинетическая теория. Большинство законов газового состояния было выведено для идеального газа. Идеальным называют газ, в котором молекулы рассматриваются как материальные точки, обладающие массой, но не имеющие при этом объёма, между которыми отсутствуют силы взаимодействия.
При больших объёмах и малых давлениях, когда расстояние между молекулами во много раз больше собственных размеров молекул, а также при высоких температурах, когда интенсивность хаотического движения молекул велика и поэтому молекулы слабо взаимодействуют между собой, складываются условия, при которых реальный газ можно с некоторым приближением считать идеальным.
Закон Бойля — Мариотта. Английский ученый Бойль и независимо от него несколько позднее французский физик Мариотт на основании экспериментов пришли к выводу о том, что объем данной массы газа и его давление находятся в обратно пропорциональной зависимости.
ГБО 4 поколения . Давление газа на редукторе должно быть? Как зависит время впрыска от давления?
Эта зависимость между давлением и объемом газа при постоянной температуре выражается формулой:
где V1 и Р1 – объем и абсолютное давление газа до их изменения; V2 и Р2 – то же, после изменения.
Из данной формулы можно получить следующие математические выражения:
Из последней формулы следует, что произведение давления данной массы газа на его объем постоянно, если температура газа не меняется.
Закон имеет практическое применение в газовом хозяйстве. Он позволяет определять объем газа при изменении его давленная и давление газа при изменении его объема при условии, что температура газа остаётся постоянной.
Чем больше при постоянной температуре увеличивается объем газа, тем меньше становится его плотность. Зависимость между объёмом газа и его плотностью при постоянной температуре выражается формулой
где V1 и V2 – объемы, занимаемые газом; ρ1 и ρ2 – плотности газа, соответствующие этим объемам.
Если в формуле (1) заменим отношение объемов газа отношением их плотностей, то на основании формулы (4) можно получить.
Из формулы (5) можно сделать вывод, что при одной и той же температуре плотности газов прямо пропорциональны давлениям, под которым находятся эти газы, т.е. плотность газа (при постоянной температуре) будет тем больше, чем больше будет его давление.
Пример. Объем газа при давлении 760 мм.рт.ст. и при температуре 0°С составляет 300 м 3 . Какой объем займет этот газ при абсолютном давлении, равном 1520 мм.рт.ст. и при той же температуре?
760 мм.рт.ст. = 101 320 Па = 101,3 кПа;
1520 мм.рт.ст. = 202 630 Па = 202,6 кПа.
Подставляем заданные значения V1, Р1, и Р2 в формулу (2):
Р1 = 101,3 кПа; V1 = 300 м 3 ; Р2 = 202,6 кПа;
101,3 х 300 = 202,6 V2, откуда V2 = (101,3 х 300)/202,6 = 150 м 3 .
Какое давление газа на форсунках?!
Закон Гей-Люссака. Французский химик Гей-Люссак впервые установил зависимость объема газа от температуры при постоянном давлении. Сущность этой зависимости заключается в том, что при постоянном давлении относительное изменение объема данной массы газа прямо пропорционально изменению температуры. Математически эта зависимость между объемом и температурой газа при постоянном давлении записывается следующим образом:
где V – объем газа, м 3 ; Т – абсолютная температура, К.
Из формулы (6) следует, что если определенный объем газа нагревать при постоянном давлении, то его объем изменится во столько раз, во сколько раз изменится его абсолютная температура.
Многочисленные опыты показывают, что при нагревании газов на 1 градус при постоянном давлении их объем увеличивается на постоянную величину, равную 1/273,2 первоначального их объема. Эта величина называется термическим коэффициентом объемного расширения и обозначается α = 1/273,2 град -1 .
С учетом этого закон Гей-Люссака можно сформулировать так: объем данной массы газа при постоянном давлении увеличивается линейно при повышении температуры
где Vt и V0 – объемы газа при конечной и начальной температурах, м 3 ; t и Т – начальная и конечная температуры, о С, К; α – термический коэффициент объёмного расширения.
Из формулы (9) следует, что объем газа при постоянном давлении прямо пропорционален его абсолютной температуре.
Закон Шарля. Согласно закону Шарля, давление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре. Из этого закона следует, что отношение давлений массы газа при постоянном объеме равно отношению его абсолютных температур. Закон выражается следующей формулой:
где Р1 и Р2 – абсолютные давления; Т1 и Т2 – абсолютные температуры газа, К.
Из формулы (10) можно сделать вывод, что при постоянном объеме давление газа при нагревании увеличивается во столько раз, во сколько раз увеличивается его абсолютная температура.
Пример 1. При температуре газа 27°С его давление равно 4 МПа (40 кгс/см 2 ). Каково будет избыточное давление этого газа при температуре 47°С?
Начальная абсолютная температура газа равна: ,
конечная абсолютная температура газа равна: .
Атмосферное давление примем равным 0,1 МПа (1 кгс/см 2 ), тогда абсолютное давление газа до нагревания будет: .
Искомое абсолютное давление газа Р2 по формуле (10) равное:
Следовательно, избыточное давление газа после нагревания его до 47°С равно:
Пример 2. Сжатый газ в баллоне при температуре 7°С имел избыточное давление 0,9МПа. После нагревания давление в баллоне повысилось до 1,1 МПа. До какой температуры был нагрет газ?
Начальная абсолютная температура газа: .
Начальное абсолютное давление газа: .
Конечное абсолютное давление газа: .
Из формулы (10) после преобразования ее относительно неизвестной Т2 получаем:
Следовательно, газ в баллоне был нагрет до температуры 63°С.
Закон Авогадро. Итальянский ученый Амадео Авогадро выразил предположение, что различные газы, занимающие одинаковые объёмы при равных условиях (одинаковые давление и температура), содержат одинаковое число молекул.
Это число для одной грамм-молекулы (1 моль) любого газа составляет около N = 6,064 х 10 23 и называется числом Авогадро. В дальнейшем было экспериментально установлено, что 1 грамм-молекула любого газа при нормальных условиях занимает объем 22,4л.
В Международной системе единиц производной является величина, в 1000 раз большая моля, она называется киломоль и обозначается кмоль. 1 кмоль любого газа при нормальных условиях (0°С и 101,3 кПа) занимает объем 22,4 м 3 . Зная эту величину, можно определить плотность любого газа по формуле
где М — масса 1 кмоля газа, кг.
Пример 1. Определить плотность метана при нормальных условиях (О о С и 101,3 кПа):
Пример 2. В баллоне находится 100 кг жидкого этана. Определить объем паров этана, полученных при его полном испарении в нормальных условиях.
Решение. Сначала определяют число киломолей этана:
п = 100 : 30,07 = 3,33 (здесь 30,07 – молекулярная масса этана).
Зная, что 1 киломоль этана при испарении, т.е. в газообразном состоянии, занимает объем 22,4 м 3 , находят объем паров этана от испарения всего его количества:
V = 22,4 х 3,33 = 74,63 м 3 .
Уравнение Клапейрона — Менделеева. При одновременном изменении объема, давления и температуры газа справедливы законы и Бойля — Мариотта и Гей-Люссака.
Французский ученый Клапейрон пришел к выводу о существовании для газов некоторой универсальной функции. Русский ученый Д.И. Менделеев вывел в более общем виде уравнение состояния идеальных газов, объединив уравнения законов Бойля — Мариотта и Гей-Люссака в одно общее математическое уравнение идеального газа, которое называется уравнением Клайперона—Менделеева:
Величина обозначается буквой “R” называется газовой постоянной. Подставляя обозначение газовой постоянной в формулу (12), получаем выражение:
Это уравнение закона газового состояния связывает все три основных параметра данного количества газа: объем, абсолютное давление и абсолютную температуру, и оно относится к 1 молю газа.
Из уравнения следует, что для определенного количества газа произведение его объема на абсолютное давление равно произведению газовой постоянной на абсолютную температуру газа. Числовое значение газовой постоянной зависит от величин параметров, входящих в уравнение (13).
В Международной системе универсальная газовая постоянная для 1 кмоля равна:
где 101325 – нормальное давление, Па.
Уравнением Клапейрона — Менделеева часто пользуются при пересчете характеристик газа. Формулы (14) и (15), предназначенные для пересчета параметров, характеризующих состояние газа в нормальных и стандартных условиях, получены путем соответствующих, преобразований выражения .
где VН Vст – объём газа при нормальных и стандартных условиях, м 3 ; Vt – объём газа при реальных условиях, м 3 ; Pt – давление газа при реальных условиях, Па; Р – давление газа при нормальных и стандартных условиях (101325 Па).
Закон Дальтона. Смеси газов (паров), близких по своим свойствам к идеальным, характеризуются аддитивностью парциальных давлений. Аддитивность (от лат. additivus – прибавляемый), свойство объекта, по которому величина всего объекта равна сумме величин частей объекта при любом разбиении. Так, масса тела равна сумме масс его частей.
Парциальным давлением компонента ρi газовой смеси называется то давление, которое этот компонент оказывал бы, если бы из смеси удалить все другие компоненты при сохранении первоначальных объема и температуры системы. Закон аддитивности записывается следующим образом:
где π — общее давление смеси газов (паров). Из уравнения следует, что
Подставив это выражение в уравнение (17), получим
т.е. парциальное давление компонента равно давлению системы, умноженному на мольную долю этого компонента в газовой фазе.
Пример. Известен молярный состав смеси газов, %: метан – 90, этан – 5, пропан – 2, азот – 2, бутаны – 1. Смесь находится под давлением 12 МПа. Требуется определить парциальное давление компонентов смеси.
Решение. Пользуясь уравнением, вычисляют парциальное давление компонентов:
Законы реальных газов. При повышении давления объем реального газа становится меньше, чем идеального. Это обстоятельство учитывают введением соответствующих поправок в законы идеальных газов.
Так, уравнение состояния реального газа можно записать в виде:
где z — коэффициент сжимаемости, являющийся функцией приведенного давления Рпр = P/Pкр и приведенной температуры Tпр = T/Ткр; Ркр и Ткр — критические давление и температура (табличные значения).
Давление насыщенных паров. Пары жидкости могут быть насыщенными и ненасыщенными. Насыщенным называется пар, находящийся в равновесии с жидкостью. Чем выше температура, тем выше давление, при котором находится данная равновесная система. Для насыщенных паров существует однозначная зависимость между давлением паров и температурой Р = f(T).
Ненасыщенными (перегретыми) парами называют пары, которые при данных температуре и давлении образуют однофазную систему. Жидкая фаза отсутствует.
Известно, что жидкость начинает кипеть при такой температуре, при которой давление её насыщенных паров Р становится равным внешнему давлению π. Давление насыщенных паров определяют по табличным данным или эмпирическим уравнениям (ур-е Антуана, Киреева).
Для определения ДНП нефтепродуктов, представляющих собой сложные смеси углеводородов различных классов, предложены графики и формулы (Кокса, Ашворта, Вильсона, BWR и др.)
Закон Рауля. Этот закон устанавливает зависимость между парциальным давлением компонента, входящего в состав раствора, его молярной концентрацией в жидкой смеси Х и упругостью пара того же чистого компонента при заданной температуре Q.
Парциальное давление компонента в жидкой смеси равно его молярной концентрации, умноженной на упругость его паров в чистом виде при данной температуре:
где р – парциальное давление компонента в растворе.
По закону Рауля, сумма парциальных давлений всех компонентов равна общему давлению над смесью или общей упругости паров смеси:
где ХnQn – молярная концентрация и упругость паров компонента соответственно.
Пример. Жидкая смесь состоит из этана –60%, пропана –25 % и изобутана –15 % (молярные доли). Требуется определить общее давление системы при температуре 10 0 С.
Решение. Сначала из рис. 2.1 (график Кокса) находим давление насыщенных паров компонентов в чистом виде при 10°С:
Затем по уравнению определим общее давление системы:
Данные этого примера показывают, что если бы указанная смесь транспортировалась в жидком виде при 10°С, то трубопровод работал под давлением 2,14 МПа.
Важным выводом, вытекающим из закона Рауля, является то, что высококипящие компоненты имеют низкую упругость, содержатся в паровой фазе в малых количествах; следовательно, их основная доля находится в жидкой фазе. Что касается низкокипящих компонентов, обладающих высокой упругостью, то они легко переходят в газовую фазу. На этом положении основана работа многих установок по частичной стабилизации газового конденсата при выветривании – ступенчатом снижении давления смеси с одновременным ее расширением.
Источник: studfile.net
Характеристика системы газоснабжения на уровне генерального плана города
Классификация газопроводов, входящих в систему газоснабжения представлена в таблице №5.
Таблица № 5. Классификация газопроводов.
| Газопроводы | Классификационный показатель |
| Наружные и внутренние | Местоположение относительно планировки поселений |
| Подземные, надземные, наземные | Местоположение относительно поверхности земли |
| Распределительные, газопроводы-вводы, вводные, продувочные, сбросные, импульсные, а также межпоселковые | Назначение в системе газоснабжение |
| Металлические и неметаллические | Материал труб |
| Природного газа, попутного газа и СУГ | Вид транспортируемого газа |
В соответствии с указаниями пункта 2.2 СНиПа 2.04.08-87 «Газоснабжение», газопроводоы по уровню давления газа в них делятся на:
Г1 – газопровод низкого давления (р ≤ 5 кПа)
Г2 – газопровод среднего давления (р ≤ 0,3 МПа)
Г3 – газопровод высокого давления второй категории (р ≤0,6 МПа)
Г4 – газопровод высокого давления первой категории (р ≤ 1,2 МПа)
(Г4 применяют только для крупных городов)
Распределительные наружные газопроводы высокого и среднего давлений выполняются чаще всего кольцевыми (газопроводы Г1). Трассирование газопроводов тесно связано с планировкой города, размещением крупных потребителей, наличием особого рода препятствий. Трассирование выполняют так, чтобы общая протяженность газопроводов была минимальной. В профиле одних и тех же улиц возможна параллельная прокладка газопроводов Г1, Г2, Г3. Следует стремиться к прокладке Г3 и Г4 по периферийной части города, где плотность населения минимальна и относительно мало подземных коммуникаций.
Газопроводы высокого и среднего давления должны обслуживать и коммунальных, и промышленных потребителей. Но для крупных промышленных предприятий, ТЭЦ допустима прокладка специальных трубопроводов либо от газораспределительной станции, либо от магистрального газопровода.
Плотность прокладки газопроводов низкого давления должна быть такой, чтобы длина газопроводов-вводов была 50-100 м.
Газорегуляторные пункты (ГРП).
Газорегуляторные пункты необходимы для связи участков газопроводов с различным рабочим давлением (Г1-Г3; Г2-Г3). Центральным элементом ГРП является регулятор давления. Кроме него ГРП может оборудоваться фильтрами, предохранительными клапанами, комплектом КИП (контрольно-измерительные приборы) и т.д. Все это в различных вариантах исполнения обычно размещается в отдельно стоящих или пристроенных зданиях и шкафах. Для отдельно стоящих ГРП должно выдерживаться удаление от сооружений различного вида 10-15 м.
Для соединения развитых кольцевых трубопроводов Г3 и Г1 (последний имеет вид единого трубопровода для всей селитебной территории) необходимо несколько сетевых ГРП, имеющих пропускную способность от 1000 до 3000 м 3 /час и радиус действия 400-800м. Сетевые ГРП располагаются в условных центрах зон обслуживания, границы которых точно установить нельзя.
Если же трубопровод Г1 представлен отдельными микрорайонными участками, то устраиваются квартальные ГРП с пропускной способностью 100-500 м 3 /час и радиусом 50-200м. Эти ГРП размещаются в отапливаемых шкафах, они обычно предназначаются для связи Г2-Г1, то есть давления на входе менее 0,3 МПа.
На рисунке 20 представлена схема централизованного газоснабжения среднего города, двухступенчатая со связью Г3-Г1. На схеме показаны сетевые ГРП.
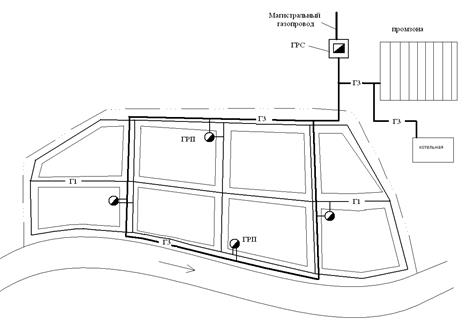
Рис.20. Схема централизованного газоснабжения.
ГРС – газораспределительная станция; Г1 – газопровод низкого давления (р ≤ 5 кПа); Г3 – газопровод высокого давления второй категории (р ≤0,6 МПа); ГРП – газорегуляторный пункт.
На полосе между красной линией квартала и линией застройки следует размещать газопровод Г1.
Источник: studopedia.su
Давление газа — формула. Формула давления газа в сосуде

Давление является одним из трех основных термодинамических макроскопических параметров любой газовой системы. В данной статье рассмотрим формулы давления газа в приближении идеального газа и в рамках молекулярно-кинетической теории.
Идеальные газы
Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.
В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.
В идеальном газе существует лишь единственный вид взаимодействия — упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.
Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.
Причина возникновения давления в газах
Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.
Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:
Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:
Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 10 23 ), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.
Формула давления газа идеального из молекулярно-кинетической теории
При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.
Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.
Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:
Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.
Формула давления из уравнения состояния

В середине 30-х годов XIX века французский инженер Эмиль Клапейрон, обобщая накопленный до него экспериментальный опыт по изучению поведения газов во время разных изопроцессов, получил уравнение, которое в настоящее время называется универсальным уравнением состояния идеального газа. Соответствующая формула имеет вид:
Здесь n – количество вещества в молях, T – температура по абсолютной шкале (в кельвинах). Величина R называется универсальной газовой постоянной, которая была введена в это уравнение русским химиком Д. И. Менделеевым, поэтому записанное выражение также называют законом Клапейрона-Менделеева.
Из уравнения выше легко получить формулу давления газа:
Равенство говорит о том, что давление линейно возрастает с температурой при постоянном объеме и увеличивается по гиперболе с уменьшением объема при постоянной температуре. Эти зависимости отражены в законах Гей-Люссака и Бойля-Мариотта.
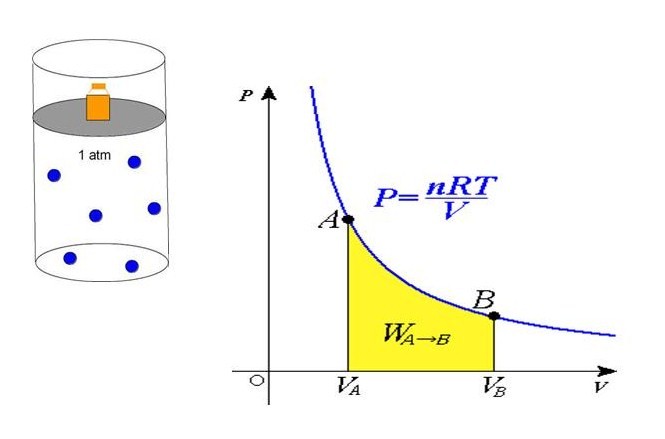
Если сравнить это выражение с записанной выше формулой, которая следует из положений МКТ, то можно установить связь между кинетической энергией одной частицы или всей системы и абсолютной температурой.
Давление в газовой смеси
Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.
Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:
- Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
- Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример задачи
Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.
Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:
Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:
Объем сосуда в кубических метрах равен 0,01 м 3 . Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.
Источник: fb.ru