Диагонали a куб с длиной стороны 1. AC ‘(показано синим) — это диагональ пространства с длиной 3 < displaystyle < sqrt >> , а AC (показан красным) — это диагональ лица и имеет длину 2 < displaystyle < sqrt >> .
В геометрия, а диагональ это отрезок присоединение двух вершины из многоугольник или же многогранник, когда эти вершины не находятся на одной край. Неформально любую наклонную линию называют диагональной. Слово диагональ происходит от древнегреческий διαγώνιος диагони, [1] «от угла к углу» (от διά- диа-, «через», «поперек» и γωνία гония, «угол», относящийся к угрюмый «колено»); его использовали оба Страбон [2] и Евклид [3] для обозначения линии, соединяющей две вершины ромб или же кубовид, [4] и позже принят на латынь как диагонус («косая линия»).
В матричная алгебра, диагональ квадрата матрица представляет собой набор записей, простирающихся от одного до самого дальнего угла.
Есть и другие нематематические применения.
ДИАГОНАЛЬ — что это такое? значение и описание
- 1 Нематематическое использование
- 2 Полигоны
- 2.1 Области, образованные диагоналями
- 2.2 Пересечения диагоналей
- 2.3 Правильные многоугольники
Нематематическое использование

Стенд основных строительных лесов на строительной площадке дома с диагональными распорками для сохранения конструкции.
В инженерное дело, диагональная скоба — это балка, используемая для крепления прямоугольной конструкции (например, строительные леса ) выдерживать толчки сильных сил; хотя диагональные скобы называются диагональными, из практических соображений они часто не соединяются с углами прямоугольника.
Плоскогубцы диагональные Кусачки для проволоки, определяемые режущими кромками губок, пересекающими стыковочную заклепку под углом или «по диагонали», отсюда и название.
А диагональная увязка это тип найтовки, используемой для связывания лонжеронов или стоек вместе, применяемых таким образом, чтобы найтовки пересекали стойки под углом.
В ассоциация футбола, то диагональ система контроля — это метод, который используют судьи и помощники судьи для позиционирования себя в одном из четырех квадрантов поля.

Диагональ — это обычное измерение Размер дисплея.
Полигоны
Применительно к многоугольник, диагональ — это отрезок соединение любых двух непоследовательных вершин. Следовательно, четырехугольник имеет две диагонали, соединяющие противоположные пары вершин. Для любого выпуклый многоугольник, все диагонали лежат внутри многоугольника, но для повторно входящие многоугольники, некоторые диагонали находятся за пределами многоугольника.
Любой п-сторонний многоугольник (п ≥ 3), выпуклый или же вогнутый, имеет п ( п − 3 ) 2 < Displaystyle < tfrac >> диагонали, поскольку каждая вершина имеет диагонали ко всем остальным вершинам, кроме себя и двух соседних вершин, или п — 3 диагонали, причем каждая диагональ делится на две вершины.
Свойства диагоналей прямоугольника
Области, образованные диагоналями
В выпуклый многоугольник, если нет трех диагоналей одновременный в одной точке внутри, количество регионов, на которые диагонали делят интерьер, определяется как
За п-угольники с п= 3, 4, . количество регионов равно [5]
1, 4, 11, 25, 50, 91, 154, 246.
Это OEIS последовательность A006522. [6]
Пересечения диагоналей
Если никакие три диагонали выпуклого многоугольника не совпадают во внутренней точке, количество внутренних пересечений диагоналей определяется как ( п 4 ) < Displaystyle < binom >> . [7] [8] Это верно, например, для любого правильный многоугольник с нечетным количеством сторон. Формула следует из того факта, что каждое пересечение однозначно определяется четырьмя конечными точками двух пересекающихся диагоналей: количество пересечений, таким образом, является количеством комбинаций п вершины по четыре за раз.
Правильные многоугольники
А треугольник не имеет диагоналей.
А квадрат имеет две диагонали равной длины, которые пересекаются в центре квадрата. Отношение диагонали к стороне равно 2 ≈ 1.414. < displaystyle < sqrt > приблизительно 1,414.>
А правильный пятиугольник имеет пять диагоналей одинаковой длины. Отношение диагонали к стороне — это Золотое сечение, 1 + 5 2 ≈ 1.618. < displaystyle < frac >> > примерно 1,618.>
Обычный шестиугольник имеет девять диагоналей: шесть более коротких равны друг другу по длине; три более длинных равны друг другу по длине и пересекаются в центре шестиугольника. Отношение длинной диагонали к стороне равно 2, а отношение короткой диагонали к стороне равно 3 < displaystyle < sqrt >> .
Обычный семиугольник имеет 14 диагоналей. Семь более коротких равны друг другу, а семь более длинных равны друг другу. Обратная сторона равна сумме обратных величин короткой и длинной диагонали.
В любом регулярном п-гон с п даже все длинные диагонали пересекают друг друга в центре многоугольника.
Многогранники
А многогранник (а твердый объект в трехмерное пространство, ограниченный двумерный лица ) может иметь два разных типа диагоналей: диагонали лица на разных гранях, соединяя несмежные вершины на одной грани; и диагонали пространства, полностью внутри многогранника (за исключением концов на вершинах).
Так же как треугольник не имеет диагоналей, поэтому тетраэдр (с четырьмя треугольными гранями) не имеет диагоналей граней и пространственных диагоналей.
А кубовид имеет две диагонали на каждой из шести граней и четыре диагонали пространства.
Матрицы
В случае квадратная матрица, то главный или же главная диагональ — диагональная линия записей, идущая от верхнего левого угла к нижнему правому углу. [9] [10] [11] Для матрицы А < displaystyle A>с индексом строки, указанным я < displaystyle i>и индекс столбца, указанный j < displaystyle j>, это будут записи А я j < displaystyle A_ > с я = j < displaystyle i = j>. Например, единичная матрица может быть определен как имеющий элементы 1 на главной диагонали и нули в другом месте:
( 1 0 0 0 1 0 0 0 1 ) < displaystyle < begin 1 0 0 0 0 1 end >>
Диагональ от верхнего правого до нижнего левого угла иногда описывается как незначительный диагональ или антидиагональный. В недиагональный записи не на главной диагонали. А диагональная матрица это тот, у которого все недиагональные элементы равны нулю. [12] [13]
А супердиагональ вход — это тот, который находится прямо над и справа от главной диагонали. [14] [15] Так же, как диагональные записи А я j < displaystyle A_ > с j = я < displaystyle j = i>, супердиагональные элементы j = я + 1 < displaystyle j = я + 1>. Например, все ненулевые элементы следующей матрицы лежат в наддиагонали:
( 0 2 0 0 0 3 0 0 0 ) < displaystyle < begin 0 0 0 3 0 0 end >>
Точно так же субдиагональный вход — это тот, который находится непосредственно под и слева от главной диагонали, то есть запись А я j < displaystyle A_ > с j = я − 1 < displaystyle j = i-1>. [16] Диагонали общей матрицы можно указать индексом k < displaystyle k>измеряется относительно главной диагонали: главная диагональ имеет k = 0 < displaystyle k = 0>; супердиагональ имеет k = 1 < displaystyle k = 1>; поддиагональ имеет k = − 1 < displaystyle k = -1>; и вообще k < displaystyle k>-диагональ состоит из элементов А я j < displaystyle A_ > с j = я + k < Displaystyle j = я + к>.
Геометрия
По аналогии подмножество из Декартово произведение Икс×Икс любого набора Икс с самим собой, состоящий из всех пар (x, x), называется диагональю и является график из равенство связь на Икс или, что то же самое, график из функция идентичности из Икс к Икс. Это играет важную роль в геометрии; например, фиксированные точки из отображение F из Икс самому себе может быть получена пересечением графика F с диагональю.
В геометрических исследованиях идея пересечения диагонали с собой является обычным явлением, не напрямую, а путем нарушения его в пределах класс эквивалентности. Это связано на глубоком уровне с Эйлерова характеристика и нули векторные поля. Например, круг S 1 имеет Бетти числа 1, 1, 0, 0, 0, и, следовательно, эйлерова характеристика 0. Геометрический способ выразить это — взглянуть на диагональ на двухугольнике.тор S 1 xS 1 и заметьте, что он может двигаться от себя малым движением (θ, θ) к (θ, θ + ε). В общем, число пересечения графика функции с диагональю может быть вычислено с использованием гомологии через Теорема Лефшеца о неподвижной точке; самопересечение диагонали является частным случаем тождественной функции.
Смотрите также
- Нормальная форма Джордана
- Главная диагональ
- Диагональный функтор
Источник: wikidea.ru
ДИАГОНАЛЬ
ДИАГОНАЛЬ, -и, ж. 1. В математике: отрезок прямой линии, соединяющий две вершины многоугольника, не лежащие на одной стороне, или две вершины многогранника, не лежащие на одной грани. 2. Ткань с косыми рубчиками. По диагонали — наискось, не под прямым углом. Разлиновать лист по диагонали. || прилагательное диагональный, -ая, -ое (к 1 значение) и диагоналевый, -ая, -ое (ко 2 значение).
Предыдущее слово ДИАГОНАЛЕВЫЙ
Следующее слово ДИАГОНАЛЬНО
Как это будет выглядеть:
ДИАГОНАЛЬ, -и, ж. 1. В математике: отрезок прямой линии, соединяющий две вершины многоугольника, не лежащие на одной стороне, или две вершины многогранника, не лежащие на одной грани. 2. Ткань с косыми рубчиками. По диагонали — наискось, не под прямым углом. Разлиновать лист по диагонали. || прилагательное диагональный, -ая, -ое (к 1 значение) и диагоналевый, -ая, -ое (ко 2 значение).
О толковом словаре
Толковый словарь русского языка – единственный в Интернете бесплатный словарь русского языка с поддержкой полнотекстового поиска и морфологии слов.
Толковый словарь является некоммерческим онлайн проектом и поддерживается специалистами по русскому языку, культуре речи и филологии. Важную роль в развитии проекта играют наши уважаемые пользователи, которые помогают выявлять ошибки, а также делятся своими замечаниями и предложениями. Если Вы являетесь автором блога или администратором веб-сайта, Вы тоже можете поддержать проект, разместив у себя баннер или ссылку на словарь.
Ссылки на словарь русского языка допускаются без каких-либо ограничений.
Источник: www.vedu.ru
Что такое прямоугольник — это одна из основ геометрии
Сегодня мы расскажем об одной из основных геометрических фигур – ПРЯМОУГОЛЬНИКЕ.
Название это весьма говорящее, и в нем скрыто официальное определение.

Прямоугольник — это.
Прямоугольник – это четырехугольник, у которого все углы прямые, то есть равны 90 градусам.
Впервые описание этой фигуры встречается еще в Древнем Египте. Но в те времена все геометрические правила давались как неопровержимые истины, не предоставляя доказательств.
Более правильный подход появился в Древней Греции. И естественно, автором стал самый знаменитый математик той эпохи — Евклид. А прямоугольник, как и многие другие фигуры и термины, был подробно описан в его произведении «Начала».
Все тот же Евклид разделил все четырехугольники на два вида – параллелограммы (что это?) и трапеции (что это?).
У первых противоположные стороны равны и параллельны, а у вторых параллельна только одна пара сторон, и они при этом не равны.
То есть выглядит это так:
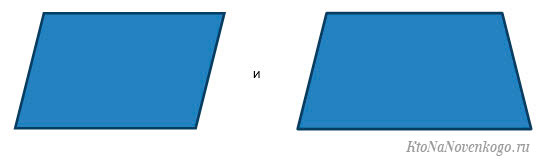
Так вот, прямоугольник в данном случае является частным случаем параллелограмма.

У этой фигуры противоположные стороны параллельны. Это первое условие по Евклиду. И к тому же они равны, что является условием номер два.
У прямоугольника есть и собственный частный случай. Когда равны не только противоположные стороны, а все. И как нетрудно догадаться, фигура эта называется квадрат.

Ну, и логично предположить, что квадрат является частным случаем параллелограмма.
Признаки прямоугольника
Признаки геометрической фигуры – это совокупность отличий, по которым ее можно выделить среди других.
В нашем случае их всего три:
- Если один из углов параллелограмма прямой, то данный параллелограмм является прямоугольником.
- Если три угла четырехугольника являются прямыми, то перед нами опять же прямоугольник. При этом нет необходимости доказывать, что четырехугольник является параллелограммом. Это промежуточное звено становится верно само по себе.
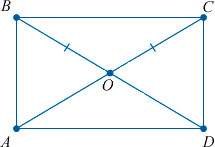
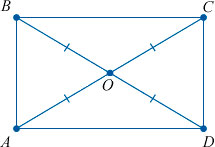
- Если диагонали параллелограмма равны между собой, то фигура точно является прямоугольником.
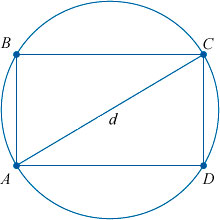
Диагонали
Как мы уже упомянули выше, диагонали прямоугольника (отрезки, соединяющие его противоположные углы) равны между собой.
Доказать это можно с помощью известной теоремы Пифагора. Она гласит, что «Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы».
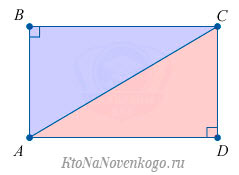
В нашем случае гипотенузой является диагональ прямоугольника, которая делит его на два равных прямоугольных треугольника. И теорема Пифагора выглядит следующим образом:
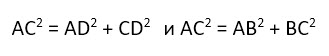
Свойства прямоугольника
К свойствам относятся следующие утверждения:
-
Прямоугольник является параллелограммом, а значит имеет все присущие ему свойства.
-
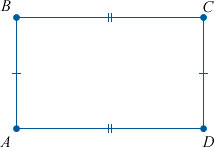
У него равны противоположные стороны.
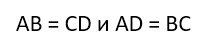
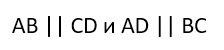

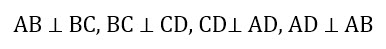
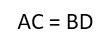
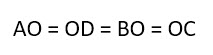
Периметр и площадь
Для того чтобы определить периметр прямоугольника, надо просто сложить длины всех его четырех сторон.

Но с учетом того, что попарно они равны, то конечная формула может выглядеть более просто:
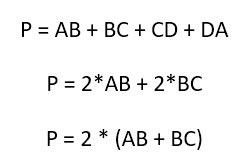
Площадь прямоугольника вычисляется также весьма просто. Надо лишь перемножить две его стороны:
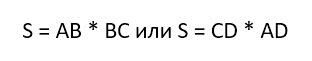
К слову, это не единственная формула для вычисления площади. Площадь также можно получить, имея значение периметра фигуры или длину его диагонали. Но эти формулы гораздо сложнее.

Вот и все, что мы хотели рассказать о геометрической фигуре ПРЯМОУГОЛЬНИК. До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Главная основа геометрии — это все же треугольник. Через него можно построить любую фигуру и доказать любую теорему.
Не согласен с утверждением, что раз один угол прямой, то перед нами точно прямоугольник. Ибо у него все противоположные стороны параллельны друг другу, а если только один угол прямой, то там и трапеция может быть.
Я бы сказала, что прямоугольник — это основа архитектуры. Все здания так или иначе используют эту фигуру в своем дизайне.
Вот за что я люблю прямоугольники, так за то, что площадь его легко найти, да и периметр, вот с трапецией сложнее, увы, но те же земельные участки больше трапеции, отсюда и земельные споры.
Ваш комментарий или отзыв
Источник: ktonanovenkogo.ru