Сразу хочу сказать, что здесь никакой воды про коаксиальные фильтры, и только нужная информация. Для того чтобы лучше понимать что такое коаксиальные фильтры , настоятельно рекомендую прочитать все из категории Устройства СВЧ и антенны. коаксиальные фильтры представляют собой подобие отрезков коаксиального кабеля и обычно выполняют функции фильтра низких частот, включаемого между системой и антенной для снижения интерференции соседних сигналов и подавления боковой полосы частот.
Широкая полоса заграждения с уровнем до 45дБ достигается при использовании передаточной характеристики Чебышева. Потери в полосе пропускания 1.5дБ или меньше. Отличительными особенностями данных фильтров являются идеальное подавление гармоник и возможность работы с высокой мощностью, вплоть до 5кВт.
Маломощные, миниатюризированные варианты таких фильтров предназначены для установки в линию в радиосистему с использованием коаксиальных разъемов на обоих концах фильтра, доступных в конфигурациях TNC, и обратной полярности TNC и SMA. Всепогодная конструкция и прочный корпус позволяют устанавливать фильтр как внутри помещения, так и на улице в течение продолжительных периодов времени.
Лекция 66. Фильтр низкой частоты
Благодаря своему широкому рабочему диапазону от 30МГц до 5ГГц коаксиальные фильтры (рис. 1.11) подходят для использования в беспилотных системах, стационарной инфраструктуре, тактических радиосистемах, автомобильных радиосистемах и других системах, где необходима радиочастотная фильтрация.
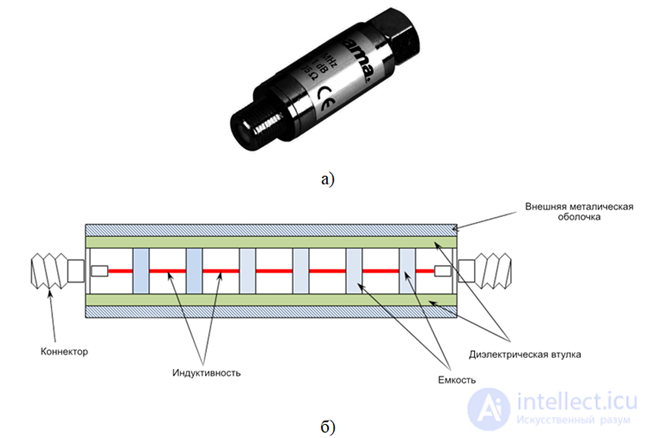Рисунок 1.11 – Коаксиальный фильтр: а) внешний вид, б) структурная схема Коаксиальные фильтры получили распространение в метровом, дециметровом и длинноволновой части сантиметрового (более 5 см ) диапазонах радиоволн. Наибольшее распространение получили фильтры на коротких отрезках.
В фильтрах на коротких отрезках линий передач используется свойство эквивалентности коротких отрезков лин ий (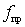
Рис.
4.2.Схемы фильтров: а —трехэлементная схема звена; б — четырехэлементная схема звена;в, г —- лестничные схемы фильтров трех- и четырехэлементные соответственно. Фильтры на коротких отрезках выполняются по трехэлементной схеме звена (рис. Об этом говорит сайт https://intellect.icu . 4.2, а, в).
Расчет коаксиальных фильтров производится методом характеристических параметров, то есть выбирается характеристическое сопротивление фильтра из условия конструктивной реализации элементов, определяются элементы схемы фильтра и геометрические размеры. Фильтры нижних частот на коротких отрезках состоят из последовательно соединенных отрезков линий передач с высоким и низким волновым сопротивлением.
ВЧ-фильтры. Часть 2. ФНЧ ФВЧ. Начинающим радиоконструкторам. Ликбез.
Конструктивно ФНЧ представляют собой жесткую коаксиальную линию, внешний проводник которой выполнен из латунной трубы диаметром D(рис. 4.5). Внутренний проводник фильтра, работающего в сантиметровом диапазоне волн, представляет собой латунный стержень, состоящий из отрезков разного диаметра d1 и d2 (рис.
4.5, а), в дециметровом и метровом диапазонах волн отрезки проводника с меньшим диаметром заменены спиральными линиями (рис. 4.5, б).
Каркас спиральной линии и диэлектрическая втулка между внутренним и внешним проводниками коаксиальной линии (параллельная емкость) изготовляется из высокочастотных диэлектриков с малыми потерями типа ПТ, полистирола, фторопласта-4, и т. д. Эквивалентная схема звена фильтра с достаточной для практики точностью может быть представлена схемой фильтра нижних частот типа К, собранного по Т- или П-образной схеме (рис. 4.5, в, г.).
Показанный на рис. 4.5, а фильтр имеет Т-образную схему звеньев. Отрезки линий длиной l1, с большим волновым сопротивлением
(рис. 4.5, а), и спиральные линии (рис.
4.5, б)эквивалентны сосредоточенным индуктивностям, отрезки линии длиной l2 с малым волновым сопротивлением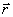 
—емкостям. Законы изменения характеристических сопротивлений для Т- и П-образных фильтров различны и показаны на рис. 4.5, в, г. Для обеспечения наилучшего согласования Zхар фильтра с сопротивлением нагрузкиZн в полосе частот от 0 до f1 необходимо, чтобы Zо было равно:
для Т-образного звена Z 0 » 1,41 Z н , (4.11) для П-образного звена Z 0 » Z н /1.41. (4.12)
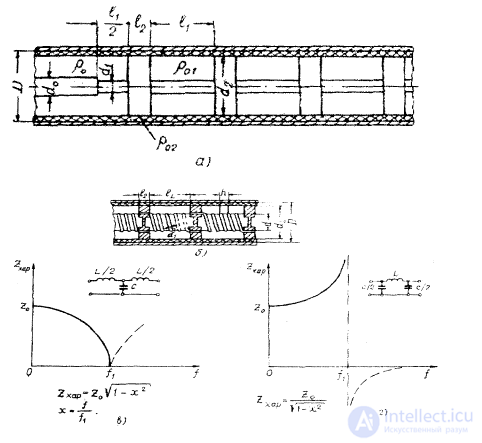
Рис. 4.5. Фильтр нижних частот: а — ФНЧ сантиметровых воли; б —ФНЧ дециметровых и метровых волн; в— зависимость Z хар от частоты для Т-образной схемы; г — для П-образной схемы.
Величины емкости и индуктивности звена связаны следующими соотношениями: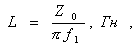 
(4.13) 
(4.14) Граничная частота f1 и сопротивление Zоравны: 
(4.15) 
(4.16) Элементы звена связаны с конструктивными размерами следующими соотношениями: 
(4.17)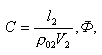 
(4.18) здесь V1, V2— скорости распространения волн в линиях 
, 
для фильтра рис. 4.5, а: V1= 3*10 10 см/сек,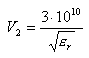 
см/сек. Коаксиальные фильтры обладают хорошими характеристиками изоляции, минимальными потерями и хорошей подавлением сигналов в нежелательных частотных диапазонах. Они широко используются в различных приложениях, включая телекоммуникации, радиосвязь, радиовещание, медицинскую технику и другие области, где требуется фильтрация сигналов в определенных диапазонах частот.
Вау!! Ты еще не читал? Это зря!
- теория фильтров , фильры сигналов , фильтр , влияние фильтра на параметры импульса ,
Статью про коаксиальные фильтры я написал специально для тебя. Если ты хотел бы внести свой вклад в развии теории и практики, ты можешь написать коммент или статью отправив на мою почту в разделе контакты. Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое коаксиальные фильтры и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Устройства СВЧ и антенны
Источник: intellect.icu
Фильтр низких частот для чего нужен тв
HPF (High Pass Filter) — фильтр низких частот, это такой фильтр в звуковой аппаратуре, который обрезает все звуковые частоты ниже частоты установки фильтра. На графике это выглядит так:
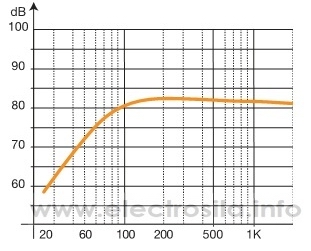
Включать этот фильтр нужно обязательно в том случае если вы подключили к усилителю акустику размером 10, 13, 16 см. Для такой акустики необходимо убрать частоты ориентировочно ниже 100 Hz, 70 Hz, 50 Hz соответственно. Обрезают низкие частоты для того, чтобы акустика не перегружалась басами которые не может полноценно отыграть. При правильной подрезке улучшается СЧ спектр, повышается скорость атаки, и снижается вероятность выхода акустики из строя. Настраивайте фильтр на слух, для каждой конкретной акустики и места её установки настройка может быть разной. Рекомендуемая частота подрезки для 16см акустики 60-80Hz
На большинстве усилителей этот фильтр включается переключателем вроде этого:
Т.е. вы можете включить либо фильтр HPF или фильтр LPF или вообще отключить фильтры. Также есть потенциометр выставляющий частоту (в данном случае 50-150 Hz хотя бывают настройки и пошире). В дорогих усилителях существует возможность включить одновременно и HPF и LPF фильтр, получив таким образом полосовой фильтр (Bandpass).
LPF (Low Pass Filter) — фильтр высоких частот, пропускающий звук ниже частоты настройки фильтра. Обычно его используют при включении сабвуфера или мидбасовых динамиков.
На графике это выглядит так:
Если вы подключаете сабвуфер и он расположен в багажнике то частота настройки фильтра должна быть не выше 70Hz, иначе велика вероятность того, что звук сабвуфера будет локализованным (вы будете слышать сабвуфер сзади, отдельно от всей музыки). Это связано с особенностями человеческого слуха-человек начинает понимать откуда идет звук частотой выше где-то 70Hz.
Поэтому сабвуфер в автомобиле стараются «обрезать» как можно ниже, чтобы казалось что звук идет «отовсюду» а не из багажника. Если ваш сабвуфер расположен спереди, под сидением например, то можно поднять частоту среза даже до 150Hz. В любом случае, задача всей настройки-добиться слитного звучания музыки в машине, в идеале вы не должны слышать отдельные динамики а только музыку в целом. Опытной настройкой фильтров добейтесь наилучшего результата.
Фильтр Bandpass (полосовой фильтр)
Позволяет включать одноврененно фильтры высоких и низких частот ограничивая диапазон с 2х сторон, устанавливая границы воспроизведения динамиков.
Актуален для 3х полосных систем с отдельными СЧ динамиками диапазон (200-4000Hz) либо для НЧ динамиков (60-200Hz)
Источник: max-audio.ru
Фильтр низких частот и переходные процессы в нем
Для анализа переходных процессов в адаптивных антенных решетках (ААР) потребуются четкие представления о свойствах и способах описания одного из самых простых и распространенных элементов радиоэлектронных цепей − RC-фильтра низких частот (ФНЧ) [6, 7]. На мой взгляд, чтобы не перегружать память, по поводу ФНЧ достаточно помнить графический образ, представленный на рис. 2.2, и уметь на этой основе записывать временные соотношения. Минимум необходимых знаний приводится мелким шрифтом.
Зависимость между входным x(t) и выходным y(t) сигналами RC-фильтра ФНЧ, полностью определяющая его свойства, проще всего описывается уравнением в операторной форме [6]:
или (1 + Tфp) y(p) = Kф x(p), (2.1)
где p = − оператор дифференцирования; Кф, Тф – параметры ФНЧ: коэффициент передачи (или усиления в активном варианте фильтра) и постоянная времени, соответственно; x(p), y(p) – изображения (по Лапласу) входного и выходного сигналов. Для пассивного RC-фильтра Кф = Rн / (R + Rн), Тф = R C. Уравнение ФНЧ во временной области получается из формулы (2.1) заменой р на d/dt:
y(t) + Tф dy(t)/dt = Kф x(t). (2.2)
Если на входе ФНЧ действует ступенчатая функция то, как это видно из формулы (2.2) , при dy(t)/dt = 0 установившееся состояние на выходе ФНЧ у∞ = y(t =∞) соответствует значению Кф А, где А – это амплитуда ступеньки. Наконец, помня, что переходный процесс на выходе ФНЧ определяется экспонентой с постоянной времени Тф, легко (не по памяти, а по смыслу!) с учетом нулевого начального y | t=0= 0 и конечного y∞ = Кф А значений записать формулу:
Кроме того, если в момент подачи ступенчатой функции на выходе ФНЧ было значение у0, то понятно, что выходной процесс складывается из экспоненциального угасания начального значения и отклика ФНЧ на ступеньку
Обратите внимание на то, что уравнение (2.2) высвечивает и другую роль постоянной времени Tф – уравнивать размерности слагаемых в правой части этого уравнения и, как следствие этого, превращать показатель временной экспоненты в безразмерное отношение. Не упущу возможности высказать парадоксальную мысль, что эта никогда не упоминаемая формальная роль постоянной времени Tф важнее ее смысловой роли – отвечать за скорость протекания процессов на выходе ФНЧ. Потому, что терялся бы сам смысл* уравнений (2.1) и (2.2), а вместе с этим обесценивались бы все формальные решения. Действительно, как вычислить значение , и отличается ли оно от значения ?
| Рис. 2.3. Интегратор, охваченный отрицательной обратной связью |
Также необходимо знать (или убедиться в том), что идеальный интегратор с отрицательной обратной связью (рис. 2.3) эквивалентен ФНЧ.
Быть может, было бы даже чуть-чуть проще анализировать схему рис. 2.3 с использованием ее операторного описания, когда идеальному интегратору соответствует передаточная функция , но ради разнообразия и расширения арсенала приемов выполним анализ во временной области без перехода к изображениям сигналов. Итак, в путь! Идеальному интегратору* соответствует уравнение
С учетом очевидной взаимосвязи = x(t) – КИ y(t) оно преобразуется к виду
После дифференцирования и умножения обеих частей равенства на величину ТИ/КИ получаем дифференциальное уравнение
которое совпадает с уравнением (2.2) для ФНЧ при постоянной времени Тф = ТИ/КИ и коэффициентом передачи Кф = 1/КИ.
Простенькие упражнения для тренировки навыков и сообразительности
1. Поразмышляйте, что будет, если уравнение идеального интегратора записать в виде ? Учтите, что, с одной стороны, в формулах могут фигурировать размерные коэффициенты, которые, имея значение, равное единице, в формулах не пишутся, но присутствуют(!). А с другой – размерности входа и выхода любого функционального элемента, интегратора в частности, могут быть разными. Итог размышлений обсуждаемой формы описания интегратора, на мой взгляд, сводится к следующему. Упрощенная запись исходного уравнения возможна, но затрудняет не только понимание результатов, но и сами вычисления. Дело в том, что приходится учитывать, в каких единицах (секундах, минутах, микросекундах и т.д.) исчисляется время для подынтегральной функции, и вычислять e — t , пользуясь безразмерным временем, нормированным к этой единице.
2. Используя описания в рамках преобразования Лапласа, докажите утверждение о том, что отрицательная обратная связь превращает интегратор в ФНЧ.
3. Без вывода формулы (2.5) из элементарных физических рассуждений по поводу функционирования схемы рис. 2.3, как говорят, «на пальцах» докажите, что если на ее входе действует постоянный сигнал x(t) = A, то на выходе установится* постоянное значение y(t) = A/КИ. Тем самым формула Кф = 1/КИ будет обоснована в обход математическим выкладкам.
4. Как и в предыдущем пункте, без аналитических выкладок покажите, что если на вход схемы подана ступенчатая функция с амплитудой А и в начальный момент времени на выходе интегратора значение равно нулю, то сигнал y(t) непрерывно нарастает со снижающейся скоростью роста** и устремляется к значению A/КИ. В поисках доводов полезно «стать компьютером», моделирующим уравнение идеального интегратора дискретными разностями для моментов времени tk = k ∆t:
Для этого примите, например, КИ = 2. Если хотите*, назначьте значение ТИ. Его придется выбирать наугад. Сообразительным студенткам или студентам не надо объяснять, что в рассматриваемом случае важно не само по себе значение постоянной ТИ, а безразмерная величина: отношение ∆t/ТИ.
При реальном компьютерном моделировании ∆t/ТИ лежит в диапазоне 10 -6 ÷ 10 -3 (естественно, чем меньше это отношение, тем выше точность моделирования). Для того чтобы, исполняя роль компьютера, вам не «перегреться» и не «зависнуть», можно положить ∆t/ТИ = 0,1 (умножать проще). Амплитуду А не только можно, но и целесообразно принять за единицу потому, что при этом результат для y(t) получится универсальным: в долях А. Наконец, учтите, что начальные значения (при k = 0) равны y(t0) = 0, .
Выполните рекурсии (2.6) для четырех − шести шагов, занося результаты в табл. 2.1.
Источник: lektsia.com