Для построения изображений предмета (светящейся стрелки), получаемых с помощью тонкой собирающей линзы, фокусы и оптический центр которой заданы, мы будем использовать три вида «удобных» лучей. Лучи, параллельные главной оптической оси, преломившись в линзе, проходят через её фокус. Из обратимости хода лучей следует, что лучи, идущие к линзе через её фокус, после преломления пойдут параллельно главной оптической оси. Наконец, лучи, проходящие через оптический центр линзы, не изменяют своего направления. Они лишь испытывают параллельное смещение, которое в случае тонкой линзы невелико и им можно пренебречь.
Для построения изображения точки можно использовать любые два из трёх «удобных» лучей, ход которых через линзу известен.
1) Луч, проходящий через оптический центр линзы.
2) Луч, падающий на линзу параллельно главной оптической оси.
3) Луч, проходящий через главный фокус линзы.
Построим изображение предмета AB, который находится между фокусом и двойным фокусом тонкой собирающей линзы (рис. 7.43).
Изображения, даваемые линзой | Физика 8 класс #31 | Инфоурок
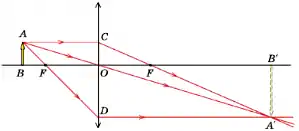
Для того чтобы получить изображение точки A, направим луч AC параллельно главной оптической оси. После преломления он пройдёт через фокус линзы F. Другой луч — AD можно направить через фокус линзы. После преломления он пойдёт параллельно главной оптической оси.
В точке пересечения этих двух преломлённых лучей будет находиться изображение А’ точки А. Таким же образом можно построить и все остальные точки изображения предмета. Но не следует думать, что изображение создаётся двумя или тремя лучами; оно формируется всем бесчисленным множеством лучей, вышедших из точки А и собравшихся в точке А’. В частности, в точку А’ попадает луч AOA’, прошедший через оптический центр О линзы.
Получившееся изображение А’В’ является действительным, увеличенным и перевёрнутым.
Теперь построим изображение предмета AB, находящегося от линзы на расстоянии, меньшем её фокусного расстояния (рис. 7.44).

Луч ВО проходит через оптический центр линзы, не преломляясь. Проведём луч BC параллельно главной оптической оси линзы. После преломления этот луч должен пройти через главный фокус линзы справа. Поскольку лучи после линзы расходятся, то изображение предмета будет мнимым; оно получается на продолжении луча CF.
Пересечение двух лучей и даёт нам искомое изображение А’В’. Оно является мнимым, прямым и увеличенным.
Допустим, необходимо построить изображение отрезка АВ, даваемое тонкой собирающей линзой, причём отрезок не перпендикулярен главной оптической оси.
Для построения будем использовать два «удобных» луча (рис. 7.45): лучи, проходящие через оптический центр линзы, и лучи, параллельные главной оптической оси.

Физика 9 класс (Урок№31 — Изображение, даваемое линзой.)
Охарактеризуем полученное изображение A’B’. Оно получилось перевёрнутым и увеличенным.
Рассмотрим случай, когда требуется построить изображение точки, расположенной на главной оптической оси. Трудность задачи заключается в том, что все три «удобных» луча сливаются в один, совпадающий с главной оптической осью. Поэтому следует определить ход произвольного луча SB (рис. 7.46), прошедшего через линзу в точке В.

Для построения преломлённого луча проведём побочную оптическую ось PQ, параллельную лучу SB. Затем построим фокальную плоскость MN и найдём точку C пересечения фокальной плоскости с побочной оптической осью. Через эту точку и пройдёт преломлённый луч ВС. Таким образом, мы построили ход двух лучей, выходящих из точки S.
После преломления в линзе эти лучи расходятся. Изображение S’ точки является мнимым, так как в ней сходятся продолжения преломлённых лучей.
Изображения, создаваемые тонкими рассеивающими линзами.
Рассмотрим построение изображений предметов в тонких рассеивающих линзах. Пусть предмет AB расположен на главной оптической оси рассеивающей линзы перед главным фокусом F (рис. 7.47).

Воспользуемся двумя «удобными» лучами. Пусть луч ВО идёт через оптический центр линзы. Он пройдёт через него, не преломляясь. Луч BC направим параллельно главной оптической оси линзы, его продолжение FC после преломления в плоскости линзы должно пройти через передний фокус.
Точка пересечения В’ луча FC и луча ВО — это мнимое изображение точки В. Поскольку предмет AB был расположен перпендикулярно главной оптической оси, то и изображение этого предмета будет расположено перпендикулярно главной оптической оси. Таким образом, мы построили изображение точки А’ на главной оптической оси. Охарактеризуем полученное изображение А’В’: оно является мнимым, уменьшенным и прямым.
Рассмотрим, каким получится изображение в тонкой рассеивающей линзе, если предмет находится между ней и фокусом. Кроме того, расположим предмет наклонно к главной оптической оси (рис. 7.48).

Направим к плоскости линзы луч AK в направлении предмета. Поскольку луч AK не принадлежит к «удобным» лучам, то для построения его хода проведём побочную оптическую ось CD, параллельную лучу АК. Найдём точку пересечения левой фокальной плоскости с побочной оптической осью. Это будет точка C — точка побочного фокуса.
Соединим точку C с точкой К — это будет продолжение преломлённого луча, который в рассеивающей линзе должен расходиться после плоскости линзы. Это означает, что изображение точки В будет мнимым и его можно получить, если провести луч ВО, проходящий через оптический центр линзы (точку О). Этот луч пересечёт луч CK в точке В’, которая и будет изображением точки В. Точка А’ получена на пересечении луча CK и главной оптической оси линзы. Охарактеризуем полученное изображение А’В’: оно является мнимым и уменьшенным.
Теперь мы можем сделать обобщающий вывод: в случае тонкой рассеивающей линзы изображение предмета всегда мнимое и уменьшенное.
Наконец, рассмотрим случай, когда необходимо построить изображение точки S, находящейся на главной оптической оси рассеивающей линзы (рис. 7.49).

Направим из точки S произвольный луч на плоскость линзы. Построим побочную оптическую ось PQ, проходящую параллельно лучу, проходящему через оптический центр линзы. Эта побочная оптическая ось пересечёт левую фокальную плоскость в точке P — побочном фокусе. Изображение точки S, будет лежать на продолжении луча PB в месте его пересечения с главной оптической осью.
Увеличение линзы.
Изображение, даваемое тонкой линзой, обычно отличается своими размерами от размеров предмета. Различие размеров предмета и изображения характеризуют такой физической величиной, как линейное увеличение.
Линейным увеличением линзы называют отношение линейного размера изображения к линейному размеру предмета.

Для определения линейного увеличения линзы обратимся к рисунку 7.43. Если высота предмета AB равна h, а высота изображения А’В’ — H, то будет линейным увеличением.
Из подобия треугольников OAB и OA’В’ следует, что  , т.е.
, т.е. 

Следовательно, линейное увеличение линзы равно

Используя подобие треугольников OCF и FA’В’, можно получить другую формулу для увеличения линзы:
Вопросы:
1. Какие «удобные» лучи используют для построения изображения предмета в линзе?
2. Приведите примеры построений изображений предмета, создаваемых тонкими собирающими линзами. Охарактеризуйте полученные изображения.
3. Приведите примеры построений изображений предмета, создаваемых тонкими рассеивающими линзами. Охарактеризуйте полученные изображения.
4. Какую физическую величину называют линейным увеличением линзы?
Вопросы для обсуждения:
1. Как, используя в качестве источника света Солнце, оценить фокусное расстояние тонкой собирающей линзы?
2. Почему в тонкостенном стакане с водой ложечка кажется увеличенной?
3. C помощью линзы на экране получено изображение пламени свечи. Изменится ли размер изображения на экране, если линзу заменить тонкой непрозрачной пластинкой с малым отверстием? Сделайте необходимый чертёж.
Пример решения задачи
C помощью тонкой собирающей линзы с фокусным расстоянием 6 см рассматривают монету, диаметр которой равен 1,25 см, и получают её мнимое изображение, диаметр которого равен 5 см. На каком расстоянии от линзы находится монета?








Ответ: d = 4,5 см.
Упражнения:
1. На рисунке 7.51 показан ход луча через линзу. Определите графически положение её фокусов.



2. Нa рисунке 7.52 показаны: AB — предмет, A’B’ — изображение, даваемое линзой. Определите графически положение оптического центра линзы и её фокусов.



3. На рисунке 7.53 показаны положение главной оптической оси линзы, источник света S и его изображение S’ в линзе. Найдите с помощью построения положение оптического центра линзы и её фокусов. Определите тип линзы.






4. Изображение миллиметрового деления шкалы, расположенной перед линзой на расстоянии d = 12,5 см, имеет на экране длину L = 8 см. На каком расстоянии от линзы находится экран? Чему равна оптическая сила линзы?
5. В 15 см от двояковыпуклой линзы с оптической силой 10 дптр поставлен перпендикулярно оптической оси предмет высотой 2 см. Найдите положение и высоту изображения.
Источник: xn—-7sbbfb7a7aej.xn--p1ai
Почему для получения правильного изображения кадр или слайд в проекторе надо устанавливать «вверх ногами»?
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
- Обратная связь
- Правила сайта
Источник: www.soloby.ru
Физика — изображения, даваемые линзой

Концепция линз является одним из фундаментальных элементов оптики, физики, и инженерных наук. Линзы используются в широком спектре приборов, начиная от очков и камер до микроскопов и телескопов. В своей простейшей форме, линза представляет собой прозрачный объект с изогнутой поверхностью, который может изменять направление падающих на нее лучей света. Изображения, создаваемые линзами, могут быть увеличены или уменьшены, и они могут быть фокусированными или нефокусированными, что делает линзы незаменимыми инструментами во многих областях.
Линзами называют прозрачные тела, ограниченные с двух сторон сферическими поверхностями.
Линзы бывают двух видов — выпуклые и вогнутые.
Линза, у которой края намного тоньше, чем середина, является выпуклой.
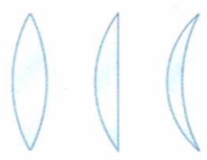
Линза, у которой края толще, чем середина, является вогнутой.

Прямая, проходящая через центры сферических поверхностей, ограничивающих линзу, называется оптической осью.
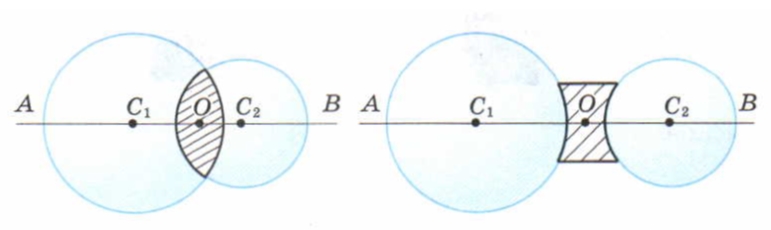
Собирающая линза
Если мы направим световые лучи, идущие параллельно оптической оси, на выпуклую линзу, то после их прохождения через линзу они сойдутся в одной точке. Эта точка, называемая фокусом линзы, является результатом фокусировки лучей и находится на оптической оси.
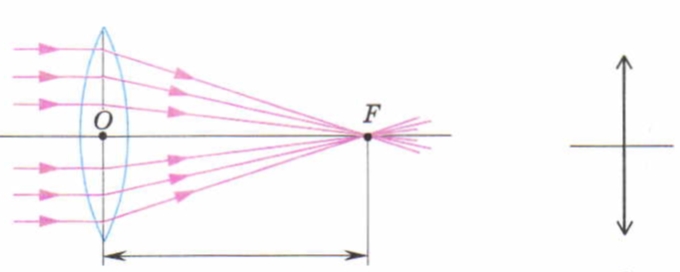
Справа на рисунке показано, как схематично изображают выпуклую линзу.
У каждой выпуклой линзы два фокуса — по одному с каждой стороны.
Расстояние от линзы до её фокуса называется фокусным расстоянием линзы и обозначается буквой F.
Выпуклая линза называется собирающей линзой.
Рассеивающая линза
Вогнутая линза обладает обратными оптическими свойствами по сравнению с собирающей линзой.
Если мы направляем на вогнутую линзу лучи света, которые параллельны оптической оси, то они будут рассеиваться в разные стороны, а не фокусироваться в одной точке, как это происходит с лучами света, падающими на собирающую линзу.
Поэтому у вогнутой линзы нет одной точки, которую можно назвать фокусом. Однако, если мы продолжим лучи, которые после прохождения через линзу идут под углом к оптической оси, то они в конечном итоге пересекутся в одной точке за линзой.
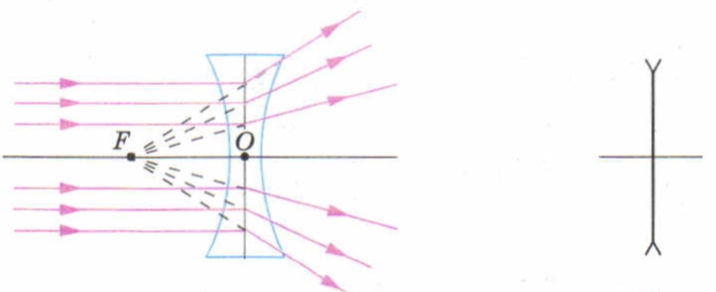
Эта точка называется мнимым фокусом.
Справа на рисунке показано, как схематично изображают вогнутую линзу.
Вогнутая линза называется рассеивающей линзой.
Изображения, даваемые собирающей линзой
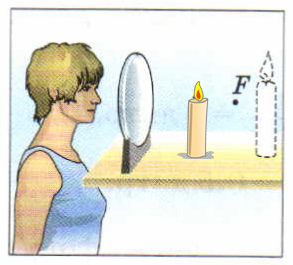
1. Предмет находится между собирающей линзой и фокусом (0
Чтобы построить изображение предмета, находящегося между фокусом и собирающей линзой, нужно воспользоваться следующей схемой для каждой точки, которую мы хотим отобразить.
Проводим два луча: один идёт через центр линзы, другой рисуется параллельно оптической оси. Луч, проходящий через центр линзы, не преломляется. Луч, который идёт параллельно оптической оси, после преломления в линзе, пройдёт через фокус.