1. Маша включает телевизор. Телевизор включается на случайном канале. В это время по девяти каналам из сорока пяти показывают новости. Найдите вероятность того, что Маша попадет на канал, где новости не идут.
2. На тарелке 16 пирожков: 7 с рыбой, 5 с вареньем и 4 с вишней. Юля наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
3. Родительский комитет закупил 30 пазлов для подарков детям на окончание учебного года, из них 12 с картинками известных художников и 18 с изображениями животных. Подарки распределяются случайным образом. Найдите вероятность того, что Вове достанется пазл с животным.
4. Игральную кость с 6 гранями бросают дважды. Найдите вероятность того, что оба раза выпало число, большее 3.
5. В чемпионате по гимнастике участвуют 50 спортсменок: 17 из России, 22 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
Мониторное безумие Проверка и обслуживание мониторов Продажа мониторов
6. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.
7. В среднем из 1500 садовых насосов, поступивших в продажу, 12 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
8. Фабрика выпускает сумки. В среднем из 300 сумок, поступивших в продажу, 18 сумок имеют скрытый дефект. Найдите вероятность того, что случайно выбранная сумка окажется без скрытых дефектов.
9. Конкурс исполнителей проводится в 3 дня. Всего заявлено 40 выступлений — по одному от каждой страны. В первый день 12 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?
10. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Биолог» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Биолог» проиграет жребий ровно один раз.
11. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 10 очков. Результат округлите до сотых.
12. В среднем из 500 садовых насосов, поступивших в продажу, 2 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
13. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что решка выпадет ровно два раза.
14. Конкурс исполнителей проводится в 3 дня. Всего заявлено 75 выступлений — по одному от каждой страны. В первый день 33 выступления, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?
15. Фабрика выпускает сумки. В среднем на 190 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
16. В чемпионате по гимнастике участвуют 56 спортсменок: 10 из Литвы, 25 из Латвии, остальные — из Эстонии. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Эстонии.
17. Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию А = ?
18. В классе 21 учащийся, среди них два друга — Вадим и Олег. Класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Вадим и Олег окажутся в одной группе.
19. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Труд» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Труд» выиграет жребий ровно один раз.
20. На олимпиаде по русскому языку участников рассаживают по трём аудиториям. В первых двух аудиториях сажают по 110 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчёте выяснилось, что всего было 400 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
21. На борту самолёта 25 мест рядом с запасными выходами и 17 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир Л. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру Л. достанется удобное место, если всего в самолёте 200 мест.
22. В группе туристов 4 человека. С помощью жребия они выбирают двух человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдёт в магазин?
23. На олимпиаде по русскому языку участников рассаживают по трём аудиториям. В первых двух аудиториях сажают по 120 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчёте выяснилось, что всего было 400 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
24. На борту самолёта 21 мест рядом с запасными выходами и 15 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир К. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру К. достанется удобное место, если всего в самолёте 450 мест.
25. В ящике лежат одинаковые на вид ручки: 1 красная, 8 черных и 6 синих. Вася выбирает наугад одну ручку. Найдите вероятность того, что эта ручка окажется синей.
26. В группе туристов 6 человек. С помощью жребия они выбирают трёх человек, которые должны идти в село в магазин за продуктами. Турист К. хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что К. пойдёт в магазин?
27. На экзамене 40 билетов. Сеня не выучил 8 из них. Найдите вероятность того, что ему попадется выученный билет.
28. Маша включает телевизор. Телевизор включается на случайном канале. В это время по трем каналам из тридцати показывают телевикторины. Найдите вероятность того, что Маша попадет на канал, где телевикторины не идут.
29. В классе 9 учащихся, среди них два друга — Михаил и Андрей. Класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Михаил и Андрей окажутся в одной группе.
30. Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию А = «сумма очков равна 9»?
Ответы
1) 0,8
2) 0,25
3) 0,6
4) 0,25
5) 0,22
6) 0,125
7) 0,992
8) 0,94
9) 0,35
10) —
11) 0,08
12) 0,936
13) 0,375
14) 0,28
15) 0,96
16) 0,375
17) 3
18) 0,3
19) 0,375
20) 0,45
21) 0,21
22) 0,5
23) 0,4
24) 0,08
25) 0,4
26) 0,5
27) 0,8
28) 0,9
29) 0,25
30) 2
Источник: 4ege.ru
ОГЭ, Математика.
Геометрия: Задача №11F101
Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
3) Площадь трапеции равна произведению средней линии на высоту.
Решение задачи:
Рассмотрим каждое утверждение.
1) Есть теорема об окружности, описанной около треугольника. Т.е. утверждение верно.
2) По свойству квадрата это утверждение верно.
3) Площадь трапеции равна произведению средней линии на высоту. Это утверждение тоже верно.
Присоединяйтесь к нам.
Вы можете поблагодарить автора, написать свои претензии или предложения на странице ‘Про нас’
Другие задачи из этого раздела
Задача №32ED6D

Радиус окружности с центром в точке O равен 29, длина хорды AB равна 40 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
Задача №0E2BF9
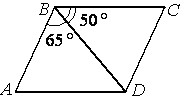
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
Задача №1A8C8D
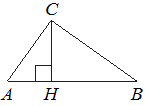
На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=4, BH=64. Найдите CH.
Задача №20702A

В треугольнике ABC угол C прямой, BC=8, sinA=0,4. Найдите AB.
Задача №FF47FC
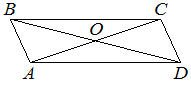
Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=12, BD=20, AB=7. Найдите DO.
(2017-04-16 14:12:05) Троишник: СПАСИБ. (2016-02-03 13:23:08) : 🙂 (2015-12-17 10:05:01) : КЛАСС (2015-12-06 12:50:43) Пятерка: :* (2015-12-06 12:50:24) Ангелочек: СУПЕР. )))
Найти задачу

Хочу получать новые решения
Источник: otvet-gotov.ru
Решение задач про выбор деталей
В ящике находится $K$ стандартных и $N-K$ бракованных деталей (всего $N$ деталей). Наудачу и без возвращения вынимают $n$ деталей. Найти вероятность того, что будет выбрано ровно $k$ стандартных и $n-k$ бракованных деталей.

*Поясню, что значит «примерно»: вместо деталей могут фигурировать изделия, болты, телевизоры и т.п.; детали могут быть стандартными и бракованными, или годными и дефектными, или обычными и поломанными и так далее. Главное, чтобы они были ДВУХ типов, тогда один тип вы считаете условно «стандартными», второй — «бракованными» и используете формулу для решения, которую мы выведем ниже.
Сначала найдем общее число исходов — это число всех различных способов выбрать любые $n$ деталей из общего множества в $N$ деталей (без учета порядка), то есть число сочетаний $C_N^n$ (см. подробнее про сочетания).
Теперь найдем число всех способов выбрать $k$ стандартных деталей из $K$ возможных — это сочетания $C_K^k$, и одновременно число всех способов выбрать $n-k$ бракованных деталей из $N-K$ возможных — $C_^$. По правилу произведения перемножая эти числа, получим число исходов, благоприятствующих нашему событию — $C_K^k cdot C_^$.
Применяя классическое определение вероятности — поделив число благоприятствующих исходов на общее число исходов, придем к искомой формуле:
Видеоурок и шаблон Excel
Посмотрите наш ролик о решении задач про детали в схеме гипергеометрической вероятности, узнайте, как использовать Excel для решения типовых задач.
Расчетный файл Эксель из видео можно бесплатно скачать и использовать для решения своих задач.
Примеры решений задач о выборе деталей/изделий
Пример 1. В партии из 12 изделий 5 изделий имеют скрытый дефект. Какова вероятность того, что из взятых наугад 4 изделий 2 изделия являются дефектными?
Популярная задача из методички, в которой меняются только цифры, а вариантов множество. С помощью данного решения и калькулятора ниже для числовых расчетов, вы легко получите полное решение задачи. Для разнообразия сделаем подробное пояснение.
Начинаем решение задачи с ввода события $A = $ (Из взятых наугад 4 изделий 2 изделия являются дефектными) и общей формулы для нахождения вероятности. Так как речь идет о выборе объектов из совокупности, используем классическое определение вероятности $P(A)=m/n$, где $n$ — общее число всех равновозможных элементарных исходов, а $m$ — число исходов, благоприятствующих событию $A$.
Сначала найдем общее число исходов — это число способов выбрать любые 4 изделия из партии в 12 изделий. Так как порядок выбора несущественнен, применяем формулу для числа сочетаний из 12 объектов по 4: $n=C_^4$.
Теперь переходим к числу благоприятствующих событию исходов. Для этого нужно, чтобы из 4 выбранных изделий 2 были дефектные (выбираем любые 2 дефектные изделия из 5 $C_5^2$ способами) и еще 2 — стандартные (выбираем любые 2 стандартные изделия из 12-5=7 имеющихся в партии $C_7^2$ способами). Тогда всего способов выбрать 2 дефектных и 2 обычных изделия из партии будет $m = C_5^2 cdot C_7^2$.
Нужная вероятность равна:
Пример 2. В ящике 16 стандартных и 7 бракованных деталей. Наудачу извлечены 6 деталей. Найти вероятность того, что среди извлеченных ровно 4 стандартных детали.
Подставляем в формулу (1) значения: $K=16$ стандартных деталей, $N-K=7$ бракованных деталей, итого $N=16+7=23$ всего деталей в ящике. Из ящика извлекают $n=6$ деталей, из них должно быть $k=4$ стандартных и соответственно, $n-k=6-4=2$ бракованные. Получаем нужную вероятность:
Пример 3. В партии из 12 изделий 8 стандартных. Найти вероятность того, что среди 3 наугад взятых есть хотя бы одно нестандартное.
Эта задача самую малость сложнее предыдущих. В ней помимо исходного события
$A = $ (Среди 3 наугад взятых изделий есть хотя бы одно нестандартное),
введем еще противоположное ему событие, которое можно записать как
$overline = $ (Все три выбранные изделия стандартные).
Тогда вероятность искомого события (что будет хотя бы одно нестандартное изделие из 3), равна:
Пример 4. Мастер для замены получил 8 однотипных деталей, из которых 3 бракованные. Он заменил 2 детали. Найти вероятность того, что замененными оказались годные детали.
Подставляем в формулу (1) значения: $K=8-3=5$ годных деталей, $N-K=3$ бракованных, $N=8$ всего деталей у мастера. Выбираем для замены $n=2$ детали, и обе они должны оказаться годными, то есть: $k=2$, $n-k=0$. Приходим к ответу:
Спасибо за ваши закладки и рекомендации
- Онлайн учебник по теории вероятностей
- Еще примеры решений задач по теории вероятностей
- Заказать решение теории вероятностей
Поищите готовые задачи в решебнике:
Источник: www.matburo.ru