Пространством состояния системы называется пространство, в каждой точке которого однозначно соответствует определенное состояние рассматриваемой динамической системы, а каждому процессу изменения состояния системы соответствует определенная траектория перемещения изображающей точки в пространстве.
Для описания движений динамических систем широко используется метод основанный на используемый, так называемого, фазового пространства (n мерного эвклидова пространства), по осям которого откладываются значения всех n обобщенных координат, рассматриваемой динамической системы. При этом однозначное соответствие между состоянии системы и точками фазового пространства достигается выбором числа измерений, равного числу обобщенных координат рассматриваемой динамической системы.
Обозначим параметрами некоторой системы символами z1, z2…zn, который можно рассматривать, как координаты вектора z, n мерного пространства. Такой вектор есть совокупность действительных чисел z=(z1,z2..zn). Параметры z1, z2…zn будут называться фазовыми координатами системы, а состояния (фазу системы) изобразим точкой z в фазовом пространстве. Размерность этого пространства определяется числом фазовых координат, то есть числом отобранных нами для описания системы, её существенных параметров.
Почему НЛП не работает? Барометр состояний. Шкалирование в коучинге. Как визуализировать Самокоучинг
В том случае, когда состояния системы можно охарактеризовать только одним параметром z1 (например, расстояния от пункта отправления поезда движущегося по некоторому заданному маршруту), то фазное пространство будет одномерным и отображаться в виде участка оси z.
Если состояние системы характеризуется 2умя параметрами z1 и z2 (например, движения автомобиля, выраженное углом относительно некоторого заданного направления и скоростью его движения), то фазовое пространство будет двухмерным.
В тех случаях, когда состояние системы описывается 3ьомя параметрами (например, управления скорость и ускорение), оно будет изображаться точкой в трьохмерном пространстве, а траектория движения системы будет пространственно кривой в этом пространства.
В общем случае, когда число параметров, характеризующую систему произвольно и как в большинстве сложных экономических систем значительно больше 3, геометрическая интерпретация теряет наглядность. Однако геометрическая терминология и в этих случая остается удобной для описания состояния и движения систем, в так называемом n мерном или многомерном фазовом пространстве (гипер пространстве).
Число независимых параметров системы называют числом степеней свободы или вариантностью систем.
В реальных условиях работы системы и её параметров (фазовые координаты), как правило, могут изменятся лишь в некоторых ограниченных приделах. Так скорость автомобиля ограничена приделами от 0 до 200 км в час, температура человека – от 35 градусов до 42 и т.д.
Область фазового пространства за пределы, которого не может выходить изображающая точка, называют областью допустимых состояний системы. При исследования и проектирования систем всегда исходит из того, что система находится в пределах в области её допустимых состояний.
Метод пространства состояний САУ: описание конкретной системы
Если изображающая точка выйдет за пределы этой области, то это грозит разрушением целостности системы, возможностью её распада на элементы, нарушением существующих связей, то есть полным прекращением её функционирование как данная система.
Область допустимых состояний, которую можно назвать полем системы, включает в себя всевозможные фазовые траектории, то есть линии поведения систем. Совокупность фазовых траекторий называют фазовым портретом рассматриваемой динамической системы. Во всех случаях, когда параметры системы могут принимать в определенном интервале любые значения, то есть изменяется плавно изображающая точка, которая может располагаться в любой точке внутри области допустимых состояний, при этом мы имеем дело с так называемым непрерывным пространством состояний. Однако существует большое количество технических, биологических и экономических систем, в которых ряд параметров – координат могут принимать лишь дискретные значения.
Только дискретно можно измерить количество станков в цехе, количество тех или иных органов и клеток в живом организме и т.д.
Пространство состояний таких систем должно рассматриваться как дискретное, поэтому их точка, изображающая состояние такой системы, не может находится в любом месте, области допустимых состояний, а только в определенных фиксированных точках этой области. Изменение состояния таких систем, то есть их движения, будет интерпретироваться скачками изображающей точки из одного состояния в другое, в третье и т.д. Соответственно и траектория движения изображающей точки будет иметь при этом дискретный, прерывистый характер.
Пространство состояний и классификация (опознание объектов)
Концепция представление объектов изображающими точками в многомерном пространстве нашла широкое применение в так называемой теории распознавания образов. Она представляет раздел кибернетики, в котором разрабатываются вопросы, теории и принципы построения систем, разделяющие сложные объекты и ситуации на заданные классы.
Задачами распознавания образов, то есть отнесения их к различным классам – классификации является, например, определение букв алфавита и звуков человеческой речи, узнавание людей и предметов, определение минералов, запахов и растений, диагностика заболеваний. Во всех этих случаях распознавание объекта состоит сличением его признаков с признаками некоторого эталона, хранящегося в мозгу человека или в памяти распознающего автомата.
Если приставить каждый признак объекта, подлежащего к опознанию в виде которого численного показателя (размер, вес, угол, насыщенность цвета, количество элементов и т.п.), то описание объектов будет сводится к некоторому конечному набору чисел, соответствующих количественных значением существенных признаков. Если принять каждое из этих чисел в качестве координаты в многомерном пространстве признаков, то объект будет представлен в этом пространстве точкой.
Учитывая некоторую вариабельность численных значений признака приходим к представления объекта в виде более или менее компактного множества точек в гиперпространстве соответствующего множества объектов 1 класса несущественно отличающихся друг от друга. Дальнейшая процедура распознавания сводится к проблеме разделения множеств соответствующих объектам разных классов, то есть классификация объектов. Геометрически это можно приставить в виде построения в пространстве признаков гиперплоскостей отделяющих эти множества друг от друга.
Движения систем
Преобразования системы
В соответствии с положениями диалектики развития материального общества, под движением принимается все происходящие в природе и обществе процессы.
Следовательно, можно говорить о химическом движении (синтезе и разложении химических соединений), органическом движении (жизненных процессов растений и животных), движение экономических систем и т.п.
Движение любой системы представляет некоторую последовательность изменение его состояния. Характеризуется состояние системы в некоторый времени U, вектором Zj, а состояние его в последующий момент времени Ti+1 вектором Zi и можно считать что произошел переход вектора Zj в вектор Zi+1 .
Правило, согласно которому каждому элементу этого множества ставится в соответствие элемент другого множества называется оператором. Говоря о переходе в систему новое состояние, оператором будем называть правило в соответствие, с которым происходит этот переход. Значение переменной или величина, над которой совершается операция, вызывающая переход в новое состояние, называется операндом.
Новое значение переменной, то есть новое состояние, возникшая под действием оператора на операнд, носит название образа.
Под воздействия некоторого оператора происходит переходы для некоторого множества операндом. Множество переходов для множества операндов будет называться преобразованием.
Любую систему, в которой происходят те или иные изменения (преобразования), в результате которых множества реакций системы некоторым образом зависит от множества входящих воздействий, можно рассматривать как преобразователь реализующей некоторую заданную зависимость Y=f(x), где Y – множество реакций системы, а х – множество входящих воздействий.
Источник: infopedia.su
Сергучёв ПР 2. описание строения системы

Единственный в мире Музей Смайликов
Самая яркая достопримечательность Крыма

Скачать 29.37 Kb.
Федеральное государственное бюджетное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра автоматизированных систем управления (АСУ)
«ОПИСАНИЕ СТРОЕНИЯ СИСТЕМЫ»
Практическая работа №2 по дисциплине «Системный анализ»
_______________ C.А. Сергучев
профессор Кафедры автоматизированных систем управления
_______________ А.М. Кориков
Оглавление
1 Цель работы 3
2Описание функционирования системы в пространстве состояний 4
— физические (размер, цвет, объем, материал, дизайн корпуса); 4
— технические (напряжение питания, количество камер, типы разморозки); 4
— параметры производителя (компания-производитель, страна, марка, дата производства, гарантийный срок); 4
Температура в холодильнике 4
3Описание жизненных циклов 5
4Описание управлений системы 6
Источник: topuch.com
Модель системы в пространстве состояний
Для случая линейной системы с p входами, q выходами и n переменными состояния описание имеет вид:
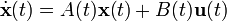
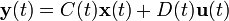
Где x— вектор состояния, элементы которого называются состояниями системы, y— вектор выхода, u— вектор управления, A — матрица системы, B— матрица управления, C— матрица выхода и D— матрица прямой связи.
Как известно, любой передаточной функции можно поставить в соответствие дифференциальное уравнение вида:
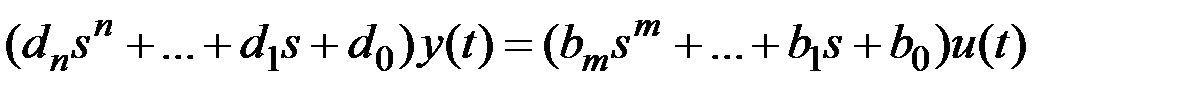
Выбор переменных состояния в принципе произволен и определяется зачастую исключительно удобством вычислений, поэтому введем следующие обозначения:
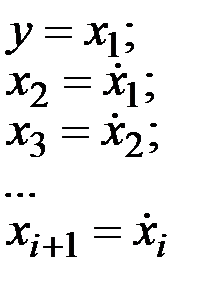
где i изменяется до n-1, тогда получим следующие уравнения
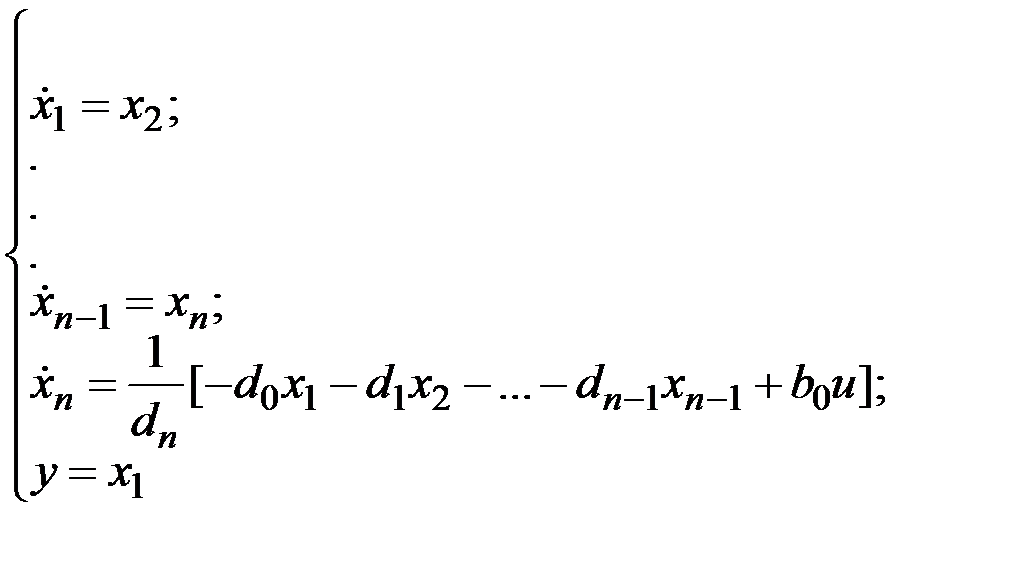
Из этой системы получим матрицы для описания системы в пространстве состояний.
В Matlab для получения матриц пространства состояния используется функция tf2ss, которая записывается в виде: [A,B,C,D]=tf2ss(num,den)
Получаем матрицы следующего вида:
-0.0001 -0.0033 -0.1733 -3.9403 -9.6332 -6.6908 0
0.0000 -0.0000 -0.0000 -0.0000 0.0625 5.7901 5.7901
Исследование системы на управляемость и наблюдаемость.
Любая САУ должна обладать свойствами управляемости и наблюдаемости.
Говорят, что система, описываемая матрицами A и B, является управляемой, если существует такое неограниченное управление u, которое может перевести систему из произвольного начального состояния x(0) в любое другое заданное состояние x(t).
Для системы с одним входом и одним выходом вводится понятие матрицы управляемости, которая имеет вид
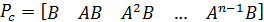
и имеет размерность n×n. Если определитель матрицы не равен нулю, то матрица является управляемой.
Калман предложил ранговые критерии. По Калману система называется вполне управляемой, если ранг матрицы управляемости равен n
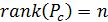
Получим матрицу управляемости и найдем ее определитель и ранг с помощью следующих вычислений в Matlab:
F 1= A * B
F 2=(A ^2)* B
F 3=(A ^3)* B
F 4=(A ^4)* B
F 5=(A ^5)* B
F 6=(A ^6)* B
PC =[ B F 1 F 2 F 3 F 4 F 5 F6]
dp= det (PC)
rp = rank (PC)
Получаем, что определитель матрицы управления не равен 0, а ранг
матрицы равен 4. Следовательно, система не является вполне управляемой. Матрицу управляемости также можно получить при помощи функции ctrb(A,B).
Система является наблюдаемой тогда и только тогда, если существует конечное время T такое, что начальное состояние x(0) может быть определено в результате наблюдения выходной переменной y(t), t T, при заданном управлении u(t).
Система является наблюдаемой, если определитель матрицы Q размерностью n×n, называемой матрицей наблюдаемости, не равен нулю, где
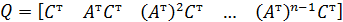
По Калману, система является вполне наблюдаемой, если ранг матрицы наблюдаемости равен n.
Находим матрицу наблюдаемости в Matlab:
F 1= A ‘* C ‘
F 2=((A ‘)^2)* C ‘
F 3=((A ‘)^3)* C ‘
F 4=((A ‘)^4)* C ‘
F 5=((A ‘)^5)* C ‘
F6 =((A ‘)^6)* C ‘
Q =[ C ‘ F 1 F 2 F 3 F 4 F 5 F6]
dq= det (Q)
rq = rank (Q)
Получаем, что определитель матрицы наблюдаемости не равен 0, ранг матрицы – 7. Следовательно, система является вполне наблюдаемой.
Цифровая модель САУ
Для получения цифровой модели САУ используем функцию c2d (sys, Ts, method). Эта функция имеет следующие параметры:
Sys – система, дискретизацию которой необходимо провести;
Ts — время квантования;
method –строковая константа, обозначающая метод дискретизации. Например, ‘ tustin ‘ –преобразование Тастина с использованием квантования по уровню.
Рассмотрим преобразование Тастина более подробно на примере корректирующего устройства системы, передаточная функция которого имеет вид:

Формула Тастина для перехода ПФ к z-преобразованию:
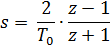
С учетом формулы Тастина проведем z-преобразование корректирующего устройства для стандартного времени квантования T0=0,025
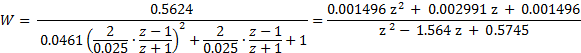
Вычисления в Matlab с помощью функции c2d дают тот же результат:
0.001496 z^2 + 0.002991 z + 0.001496
z^2 — 1.564 z + 0.5745
Sampling time: 0.025
Как известно изображения входной и выходной величины блока связаны передаточной функцией:
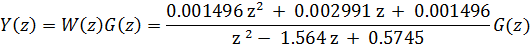
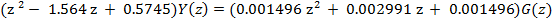
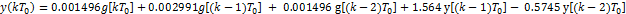
Эквивалентная схема САУ представлена на рис. 8.
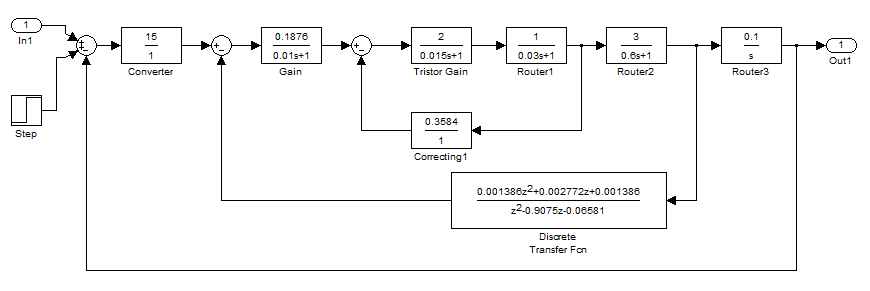
Рисунок 8 — Эквивалентная схема САУ
По разностному уравнению можно построить не только эквивалентную схему корректирующего устройства, но и подставляя конкретные k получить систему реккурентных соотношений, по которой определить значения выходного сигнала в зависимости от входного для каждого периода квантования и построить переходную функцию. Для построения переходной функции в нашем случае используем Matlab. Результат сравнения переходных функций изображен на рис. 9.
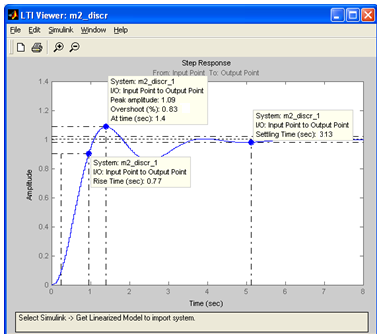
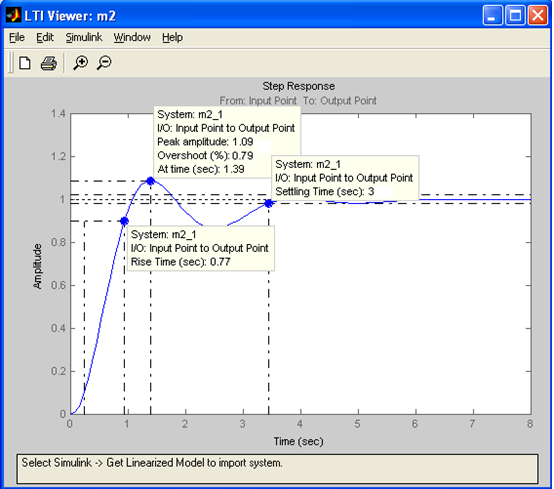
Рисунок 9 — Сравнение переходных функций систем для цифрового (вверху) и аналогового (внизу) входных сигналов
Характеристики переходной функции для цифрового сигнала: время нарастания – 0.77с, перерегулирование –0.83%, длительность переходного процесса – 5.13с. Эти характеристики отличаются от таковых, полученных в п. 2, следовательно, дискретизация системы вносит неточность в сигнал.
Источник: cyberpedia.su