По телевизору показывают 3 приключенческих фильм

Содержание

Задача. В вазе лежат 5 яблок, 4 груши и 3 мандарина. Сколько существует возможностей взять один фрукт из вазы?

Если взять яблоко, то существует 5 возможностей,

если взять грушу, то существуют 4 возможности,

если взять мандарин, то существуют 3 возможности.

Значит, чтобы взять один фрукт из всех лежащих в вазе, существует 5+4+3=12 возможностей.

Этот пример можно обобщить.

Допустим, что есть две группы: в одной k различных элементов, во второй n различных элементов. Если из первой группы какой-либо элемент можно выбрать k способами, а из второй — n способами, то выбрать один элемент из первой или второй группы можно k+n способами.

Это называется законом сложения в комбинаторике. Закон сложения также используется, если нужно выбрать элемент из трёх, четырёх и т. д. групп.

Закон сложения используется тогда, когда нужно выбрать только 1 элемент.

Чтобы использовать закон сложения:

1. нужно понять, каковы группы, из которых нужно выбрать 1 элемент;

Территория. Приключенческая Драма. Лучшие фильмы

2. нужно выяснить количество элементов в каждой группе;

3. нужно убедиться, что в различных группах, из которых выбирают элемент, нет одинаковых элементов.

Пример 1. Вика должна выбрать только один десерт из 8 видов коктейля, 5 видов мороженого и 5 видов йогурта. Сколькими способами она может выбрать десерт?

используется закон сложения, т. к. Вика должна выбрать или коктейль, или мороженое, или йогурт.

8+5+5=18. Ответ: Вика может выбрать десерт 18 способами.

При использовании закона сложения надо следить, чтобы ни один из способов выбора объекта a не совпадал с каким-либо способом выбора объекта b.
Если такие совпадения есть, то закон сложения утрачивает силу, и мы получаем лишь (k+n−m) способов выбора, где m — число совпадений.

если объект a можно получить k способами, объект b — n способами, то объект «a или b» можно получить k+n−m способами, где m — это количество повторяющихся способов.

Пример2. В группе 7 человек имеют «5» по математике, 9 человек — «5» по философии. В сессии 2 экзамена. Известно, что 4 человека сдали сессию отлично. Сколько человек имеет хотя бы одну пятерку в сессии?
Решение: 7+9−4=12.

Пример3. В магазине канцелярских товаров продаются ручки 10 различных видов, карандаши 14 различных видов и резинки 6 различных видов. Сколькими различными способами Владик может купить:

a) одну резинку? б) один карандаш и одну резинку?

в) одну резинку или один карандаш? г) все три принадлежности — ручку, карандаш и резинку?

Решение. Если в двух группах нет одинаковых элементов и если из первой группы элемент можно выбрать k способами, а из второй — n способами, то выбрать один элемент из первой или второй группы можно k+n способами.

Еще по теме: Ultra hd 4K LED телевизор 43 Hisense 43a6bg отзывы

Закон умножения:

Если элемент A можно выбрать k способами и затем второй элемент B независимо от выбора A можно выбрать m различными способами, пару элементов A и B можно выбрать k ⋅ m способами.

Как в воду глядела! Предсказания Ванги о Украине и России на 2023 год. В каком месяце война закончит

a) один элемент из всего множества можно выбрать столькими способами, сколько всего элементов данного вида;

б) используется закон умножения: 14⋅6=84 способами;

в) используется закон сложения: 6+14=20 способами;

г) используется закон умножения: 10⋅14⋅6=840 способами.

Пример4. Из опрошенных 47 молодых людей работают 19, учатся 28 и ничего не делают 3.

сколько молодых людей учится и работает?

Сколько молодых людей только учится?

Сколько молодых людей только работает?

Соответствующие множества молодых людей отображаем с помощью кругов Эйлера:

M — молодые люди, которые учатся;

S — молодые люди, которые работают:

N — молодые люди, которые ничего не делают.

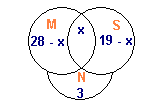
По кругам видно, что множество молодых людей делится на 4 подмножества.

Если допустить, что количество молодых людей, которые учатся и работают одновременно, равно x, то количество молодых людей, которые только учатся, равно 28−x, а количество тех, которые только работают, равно 19−x.

3. Согласно закону суммы:

(28−x)+x+(19−x)+3=47

Значит, учатся и работают одновременно 3 человек, только учатся 28−3=25 человек, а только работают 19−3=16 человек.

Из всех молодых людей учатся и работают 3 человек.

Из всех молодых людей только учатся 25 человек.

Из всех молодых людей только работают 16 человек.

Практическая работа

1. Рита хочет нарядиться на классный вечер. В её шкатулке 2 цепочки, 6 колец, и 10 браслетов. Сколькими способами она может выбрать одно украшение?

2. По телевизору в среду показывают 3 приключенческих фильмов, 6 комедий и 3 фильма ужасов.
Вычисли, сколькими различными способами можно выбрать один из всех предложенных фильмов?

3. В группе 31 человека. Из них 15 человек изучают английский язык, 16 — немецкий язык, 11 — оба языка. Сколько человек не изучают ни одного языка?

4. Каждый из 25 студентов является читателем, по крайней мере, одной из двух библиотек: колледжа и областной. Из них 15 человек берут книги библиотеке колледжа, 20 – в колледжа.

Сколько студентов:

1. Являются читателями обеих библиотек;
2. Не являются читателями областной библиотеки;
3. Не являются читателями библиотеки колледжа;
4. Являются читателями только областной библиотеки;
5. Являются читателями только библиотеки колледжа?

Инструкция.

Записать тему, закон сложения, разобрать решение задач, выполнить практическую работу.

Дата добавления: 2021-06-02 ; просмотров: 329 ; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Источник: studopedia.net

Задание №6 Выбор по одному элементу из трех групп

Изучение понятий комбинаторики: правила суммы и правила произведения, Наработка навыков решения комбинаторных задач с применением закона сложения и умножения.

Еще по теме: Потек ЖК телевизор что делать

2. Дидактическое оснащение практического занятия:

Теория по ссылке: Закон сложения в комбинаторике, Закон умножения в комбинаторике

Закон сложения	Допустим, что есть две группы: в одной k различных элементов, во второй n различных элементов. Если из первой группы какой-либо элемент можно выбрать k способами, а из второй n способами, то выбрать один элемент из первой или второй группы можно k + n способами. Закон сложения также используется, если нужно выбрать элемент из трёх, четырёх и т.д. групп.
Важно!	Закон сложения используется тогда, когда нужно выбрать только 1 элемент.
Правило использования закона сложения	Чтобы использовать закон сложения: 1. нужно понять, каковы группы, из которых нужно выбрать 1 элемент; 2. нужно выяснить количество элементов в каждой группе; 3. нужно убедиться, что в различных группах, из которых выбирают элемент, нет одинаковых элементов.
Важно!	Применение закона сложения невозможно, если есть совпадения при выборе элементов из групп
Если есть m — количество повторяющихся способов, то закон сложения (с повторениями)	Если объект a можно получить k способами, объект b n способами, то объект «a или b » можно получить k + n − m способами, где m — это количество повторяющихся способов.
Закон умножения	Если элемент A можно выбрать k способами и затем второй элемент B можно выбрать m различными способами, то пару элементов A и B можно выбрать k ⋅ m способами. Закон выполняется так же, если нужно выбирать по 1 элементу из трёх, четырёх и т.д. групп.

Задания

Задание№1. Выбор элемента из нескольких групп

Дана хочет нарядиться на классный вечер. В её шкатулке 5 цепочек, 3 колец и 12 браслетов. Сколькими способами она может выбрать одно украшение?
Решение: Закон сложения: Существуют 2 группы: в одной k различных элементов, во второй n различных элементов. Если из первой группы элемент можно выбрать k способами, а из второй — n способами, то выбрать элемент из первой или второй группы можно k + n способами. Закон также в силе, если дано большее количество групп. В данном задании 3 группы: цепочки, кольца и браслеты. Цепочку можно выбрать 5 способами; Кольцо можно выбрать 3 способами; Браслет можно выбрать 12 способами. Одно украшение можно выбрать 5+3+12=20 способами. Ответ:Одно украшение можно выбрать 5+3+12=20 способами.
Решить задание на ЯКласс	№1 Выбор элемента из нескольких групп

Задание №2 Выбор элемента из множества групп, выбор нужной группы

В школьном самоуправлении участвуют ученики разных классов. Данные обобщены в таблице:

Класс	Кол-во девочек	Кол-во мальчиков
8-й класс
9-й класс
10-й класс
11-й класс

Сколькими способами можно выбрать одного ведущего школьного мероприятия, если для роли ведущего нужно выбрать девочку из 10-ого или 9-ого класса?

Задание №3 Варианты выбора элемента из нескольких групп

Еще по теме: Срок службы va матрицы в телевизоре

По телевизору в воскресенье показывают 6 приключенческих фильмов, 5 комедий и 2 фильмов ужасов. Запиши, сколькими различными способами можно выбрать один из всех предложенных фильмов?
Решение: Используется закон сложения: Если в двух группах нет одинаковых элементов и из одной группы какой —либо элемент можно выбрать n способами, а из второй — k способами, то выбрать один элемент из первой или второй группы можно n + k способами. 6+5+2=13 Ответ:Из всех фильмов один можно выбрать 13 различными способами.
Решить задание на ЯКласс	№3 Варианты выбора элемента из нескольких групп

Задание №4 Варианты маршрутов по данному рисунку

Задание №5 Варианты выбора двух элементов (закон умножения)

На полке лежит 8 пар брюк. Игорь для путешествия из них выбирает 2 пары. Выясни, сколькими различными способами Игорь может выбрать себе брюки?
Решение: 1. Сначала Игорь может выбрать любые из всех 8 брюк. 2. Когда первый выбор сделан, для следующего остаётся 8−1=7 вариантов брюк. 3. По закону умножения: Если элемент A можно выбрать k способами и затем второй элемент B можно выбрать m различными способами, пару элементов A и B можно выбрать k ⋅ m способами. 8⋅7=56 (способами). Ответ:Игорь может выбрать брюки 56 различными способами.
Решить задание на ЯКласс	№ 5 Варианты выбора двух элементов

Задание №6 Выбор по одному элементу из трех групп

Дана корзина с конфетами разных видов. Из всех конфет 9 конфет «Буревестник», 11 конфет «Клубничные» и 3 конфеты «Белочка». Найди, сколькими способами можно выбрать 3 конфеты так, чтобы это были 1 «Буревестник», 1 «Клубничная» и 1 «Белочка»?
Решение: О Для решения задачи используется закон умножения. Если элемент A можно выбрать k способами и затем другой элемент B независимо от выбора элемента A можно выбрать m различными способами, пару элементов A и B можно выбрать k ⋅ m различными способами. Закон в силе и тогда, когда нужно выбирать по одному элементу из большего количества групп. 9⋅11⋅3=297 Ответ:Конфеты можно выбрать 297 различными способами.
Решить задание на ЯКласс	№ 5 Выбор по одному элементу из трех групп

Содержание отчета

Записать решение заданий в тетрадь, ответить на контрольные вопросы

5. Контрольные вопросы

Какой закон применим для выбора 1 элемента из нескольких групп?

Возможно ли применение закона сложения при выборе элементов из нескольких групп, если есть совпадения при выборе элементов??

Какой закон применяется при выборе нескольких элементов из одной или нескольких групп?

В чем разница применения закона сложения и уможения?

Литература и используемые интернет-ресурсы

Источник: poisk-ru.ru