Следующие логические задачи мы решим с помощью средств алгебры логики.
Задача 1. Представим такую ситуацию: по телевизору с иноптик объявляет прогноз погоды на завтра и утверждает следующее:
1. Если не будет ветра, то будет пасмурная погода без дождя.
2. Если будет дождь, то будет пасмурно и без ветра.
3. Если будет пасмурная погода, то будет дождь и не будет ветра.
Так какая же погода будет завтра?
Решение:
а ) Выделим простые высказывания и запишем их через переменные:
б) Запишем логические функции (сложные высказывания) через введенные переменные:
1. Если не будет ветра, то будет пасмурная погода без дождя:
2. Если будет дождь, то будет пасмурно и без ветра:
3. Если будет пасмурная погода, то будет дождь и не будет ветра
в) Запишем произведение указанных функций:
_
F=(A→ B (C→B (B→ C C) A) A) =
_ _ _ _
= (A v B (C v B (B v C C) A) A) =
_ _ _ _ _ _
= (A CCCA) A)=
_ _ _ _ _ _ _
РАЗГОВОРНЫЙ АНГЛИЙСКИЙ: РЕАКЦИЯ НА ПОДАРКИ.
= A (C v BBBA =
_ _ _
= AC
д) Приравняем результат единице, т.е. наше выражение должно быть истинным:
_ _ _
е) Проанализируем результат:
Логическое произведение равно 1, если каждый множитель равен 1.
Значит: A = 0; B = 0; C = 0;
Ответ: погода будет ясная, без дождя, но ветреная.
Задача 2. Трое друзей, болельщиков автогонок «Формула-1», спорили о результатах предстоящего этапа гонок.
— Вот увидишь, Шумахер не придет первым, — сказал Джон. Первым будет Хилл.
— Да нет же, победителем будет, как всегда, Шумахер, — воскликнул Ник. — А об Алези и говорить нечего, ему не быть первым.
Питер, к которому обратился Ник, возмутился:
— Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.
По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки?
Решение.
Введем обозначения для логических высказываний:
Ш — победит Шумахер; Х — победит Хилл; А — победит Алези.
Реплика Ника «Алези пилотирует самую мощную машину» не содержит никакого утверждения о месте, которое займёт этот гонщик, поэтому в дальнейших рассуждениях не учитывается.
Зафиксируем высказывания каждого из друзей:
Учитывая то, что предположения двух друзей подтвердились, а предположения третьего неверны, запишем и упростим истинное высказывание _______
( (Ш V ( X) )
2. не содержит ли она излишних усложнений.
Созданная позднее М.А.Гавриловым (1903-1979) теория релейно-контактных схем показала, что это вовсе не утопия.
Посмотрим на микросхему. На первый взгляд ничего того, что нас удивило бы, мы не видим. Но если рассматривать ее при сильном увеличении она поразит нас своей стройной архитектурой. Чтобы понять, как она работает, вспомним, что компьютер работает на электричестве, то есть любая информация представлена в компьютере в виде электрических импульсов. Поговорим о них.
С точки зрения логики электрический ток либо течет, либо не течет; электрический импульс есть или его нет; электрическое напряжение есть или его нет…В связи с этим поговорим о различных вариантах управления включением и выключением обыкновенной лампочки (лампочка тоже работает на электричестве). Для этого рассмотрим электрические контактные схемы, реализующие логические операции.
На рисунках контакты обозначены латинскими буквами А и В. Введем обозначение: 1 – контакт замкнут, 0 – контакт разомкнут. Цепь на схеме 1 с последовательным соединением контактов соответствует логической операции «И». Цепь на схеме 2 с параллельным соединением контактов соответствует логической операции «ИЛИ». Цепь на схеме 3 соответствует логической операции «НЕ».
Докажем это, рассмотрев состояния схем при различных состояниях контактов.
Попросите детей приготовить в тетради таблицу:
| Конъюнкция | Дизъюнкция | Инверсия |
Заполняйте ее по ходу объяснения материала.
Схема 1. (составляем таблицу истинности).
1. Оба контакта в положении «включено». Тогда ток через лампочку идет и она горит.
2. Первый контакт в положении «вкл», второй – в положении «выкл». Ток не идет, лампочка не горит.
3. Обратная ситуация. Лампочка не горит.
4. Оба контакта в положении выкл». Тока нет. Лампочка не горит.
Вывод: первая схема действительно реализует логическую операцию «И».
Схема 2. (составляем таблицу истинности).
1. Оба контакта в положении «включено». Тогда ток через лампочку идет и она горит.
2. Первый контакт в положении «вкл», второй – в положении «выкл». Ток идет, лампочка горит.
3. Обратная ситуация. Лампочка горит.
4. Оба контакта в положении выкл». Тока нет. Лампочка не горит.
Вывод: вторая схема действительно реализует логическую операцию «ИЛИ».
Схема 3. (составляем таблицу истинности).
В этом устройстве в качестве переключателя используется автоматический ключ. Когда тока на нем нет, пластинка замыкает контакты и лампочка горит. Если на ключ подать напряжение, то вследствие явления электромагнитной индукции пластинка прижимается и цепь размыкается. Лампочка не горит.
Вывод: третья первая схема действительно реализует логическую операцию «НЕ».
Недостатками контактных схем являлись их низкая надежность и быстродействие, большие размеры и потребление энергии. Поэтому попытка использовать такие схемы в ЭВМ не оправдала себя. Появление вакуумных и полупроводниковых приборов позволило создавать логические элементы с быстродействием от 1 миллиона переключений в секунду.
Именно такие электронные схемы нашли свое применение в качестве элементной базы ЭВМ. Вся теория, изложенная для контактных схем, была перенесена на электронные схемы. Элементы, реализующие базовые логические операции, назвали базовыми логическими элементами или вентилями и характеризуются они не состоянием контактов, а наличием сигналов на входе и выходе элемента.
Их названия (конъюнктор, дизъюнктор, инвертор) и условные обозначения являются стандартными и используются при составлении и описании логических схем компьютера.
Почему необходимо уметь строить логические схемы?
Дело в том, что из вентилей составляют более сложные схемы, которые позволяют выполнять арифметические операции и хранить информацию. Причем схему, выполняющую определенные функции, можно построить из различных по сочетанию и количеству вентилей. Поэтому значение формального представления логической схемы чрезвычайно велико.
Логические схемы необходимо строить из минимально возможного количества элементов, что в свою очередь, обеспечивает большую скорость работы и увеличивает надежность устройства.
| X | Результат |
Построение логических схем
1. Правило построения логических схем:
2. Определить число логических переменных;
3. Определить количество базовых логических операций и их порядок;
4. Изобразить для каждой логической операции соответствующий ей вентиль;
5. Соединить вентили в порядке выполнения логических операций.
Упражнение 1. Пусть Х = истина, Y = ложь. Составить логическую схему для следующего логического выражения: F = X V Y .
Ответ: 1 V 0 Y V . Вычислить значения выражения для Х=1, Y=0.
1. Переменных две: Х и Y.
2. Логических операций три: конъюнкция и две дизъюнкции.
3. Схему строим направо в соответствии с порядком логических операций:
4. Вычислим значение выражения: F = 1 , если А = 1, В = 1, С = 1 (ответ: 1)
2. F = , если А = 0, В = 1, С = 1 (ответ: 1)
3. F = V B (C V B), если А = 0, В = 1, С = 0 (ответ: 1)
Упражнение 4.
Постройте логическое выражение по логической схеме:
Ответ: F = A (( B ( V ).
Ответ: F = (C https://infopedia.su/12x728a.html» target=»_blank»]infopedia.su[/mask_link]
Решение логических задач средствами алгебры логики

1. Решение логических задач средствами алгебры логики
Иванова Юлия
2.
Разнообразие логических задач очень велико.
Способов их решения тоже немало. Но
наибольшее
распространение
получили
следующие три способа решения логических
задач:
средствами алгебры логики;
табличный;
с помощью рассуждений.
3. Решение логических задач средствами алгебры логики.
Обычно используется следующая схема решения:
1. изучается условие задачи;
2. вводится система обозначений для логических
высказываний;
3. конструируется логическая формула, описывающая
логические связи между всеми высказываниями
условия задачи;
4. определяются значения истинности этой логической
формулы;
5. из полученных значений истинности формулы
определяются значения истинности введённых
логических высказываний, на основании которых
делается заключение о решении.
4.
Задача. Представим такую ситуацию: по телевизору
синоптик объявляет прогноз погоды на завтра и
утверждает следующее:
1. Если не будет ветра, то будет пасмурная погода без
дождя.
2. Если будет дождь, то будет пасмурно и без ветра.
3. Если будет пасмурная погода, то будет дождь и не
будет ветра.
Так какая же погода будет завтра?
5.
Решение.
Выделим простые высказывания и запишем их
через переменные:
А – «Ветра нет»
В – «Пасмурно»
С – «Дождь»
Запишем сложные высказывания через введенные
переменные:
1. Если не будет ветра, то будет пасмурная
погода без дождя: A B C
2. Если будет дождь, то будет пасмурно и без
ветра: C B A
3. Если будет пасмурная погода, то будет
дождь и не будет ветра: B C A
6.
Запишем произведение указанных функций:
F ( A B C ) (C B A) ( B C A)
Упростим формулу (используем законы де Морга,
переместительный закон, закон противоречия):
F ( A B C ) (C B A) ( B C A) ( A B C ) (C B A) ( B C A)
( A B C ) ( B C A) (C B A) ( A B B C B A C A B C C A) (C B A)
A B (C B A) A B C A B B A A B C
Приравняем результат единице, т.е. наше выражение
должно быть истинным:
F A B C 1
7.
Проанализируем результат:
Логическое произведение равно 1, если каждый
множитель равен 1.
Поэтому: A 1; B 1; C 1
Значит: А=0; В=0; С=0
Ответ: погода будет ясная, без дождя, но ветреная.
8.
Задача 1. В школе-новостройке в каждой из двух
аудиторий может находиться либо кабинет
информатики, либо кабинет физики. На дверях
аудиторий повесили шутливые таблички. На первой
повесили табличку «По крайне мере, в одной из этих
аудиторий размещается кабинет информатики», а на
второй аудитории – табличку с надписью «Кабинет
физики
находится
в
другой
аудитории».
Проверяющему, который пришел в школу, известно
только, что надписи на табличках либо обе истинны,
либо обе ложны. Помогите проверяющему найти
кабинет информатики.
Ответ
9.
Задача 2. На вопрос «Кто из твоих учеников изучал
логику?» учитель ответил: «Если логику изучал
Андрей, то изучал и Борис. Однако неверно, что если
изучал Семен, то изучал и Борис». Кто же изучал
логику?
Ответ
Источник: ppt-online.org
Решение логических задач на уроках информатики.
Логические задачи имеют очень широкое распространение, т. к. они развивают умственные способности. Сначала исследователь сталкивается с набором разобщенных данных, по которым невозможно сделать какие – либо заключения. Приходится выдвигать некое предположение.
Правильность предположений, выдвинутых в ходе исследований, устанавливается путем сопоставления результатов с исходными данными. Если на этом этапе работы вскрывается несоответствие теоретических выводов фактам, исследователь отвергает предположение, выдвигает другое и начинает рассуждение заново. И так до устранения всех несоответствий.
Вы уже знаете о суперспособностях современного учителя?
![]()
Тратить минимум сил на подготовку и проведение уроков.
![]()
Быстро и объективно проверять знания учащихся.
![]()
Сделать изучение нового материала максимально понятным.
![]()
Избавить себя от подбора заданий и их проверки после уроков.
![]()
Наладить дисциплину на своих уроках.
![]()
Получить возможность работать творчески.
Просмотр содержимого документа
«Решение логических задач на уроках информатики.»
Урок по информатике: Решение логических задач
Цели: познакомить учащихся с решением логических задач.
Задачи:
- Научить учащихся решать логические задачи;
- Способствовать формированию логического мышления, интереса к изучаемому материалу.
Ожидаемые результаты обучения:Учащиеся должны знать:
- законы логики;
- правила преобразования логических выражений;
- методы решения логических задач.
Учащиеся должны уметь:
- применять законы логики;
- упрощать сложные логические выражения:
- решать логические задачи.
Ход урокаI. Оргмомент.II. Проверка домашнего задания.III. Изложение нового материала. Разнообразие логических задач очень велико. Способов их решения тоже немало. Но наибольшее распространение получили следующие три способа решения логических задач:
- средствами алгебры логики;
- табличный;
- с помощью рассуждений.
Сегодня на уроке познакомимся с решением логических задач средствами алгебры логики. Обычно используется следующая схема решения:
- изучается условие задачи;
- вводится система обозначений для логических высказываний;
- конструируется логическая формула, описывающая логические связи между всеми высказываниями условия задачи;
- определяются значения истинности этой логической формулы;
- из полученных значений истинности формулы определяются значения истинности введённых логических высказываний, на основании которых делается заключение о решении.
Задача.Представим такую ситуацию: по телевизору синоптик объявляет прогноз погоды на завтра и утверждает следующее:
- Если не будет ветра, то будет пасмурная погода без дождя.
- Если будет дождь, то будет пасмурно и без ветра.
- Если будет пасмурная погода, то будет дождь и не будет ветра.
Так какая же погода будет завтра?Решение.
- Выделим простые высказывания и запишем их через переменные:
А – «Ветра нет» В – «Пасмурно» С – «Дождь»
- Запишем сложные высказывания через введенные переменные:
- Если не будет ветра, то будет пасмурная погода без дождя:
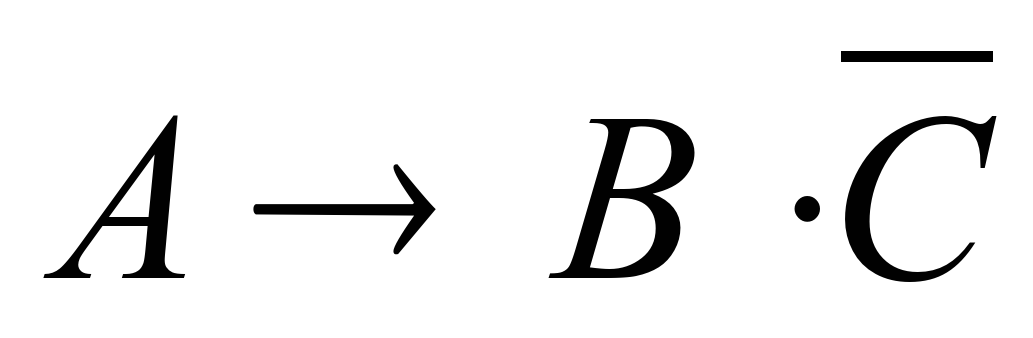
- Если будет дождь, то будет пасмурно и без ветра:
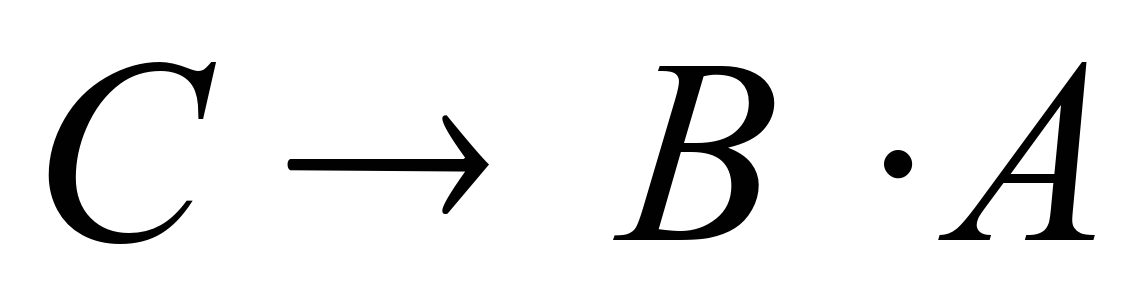
- Если будет пасмурная погода, то будет дождь и не будет ветра:
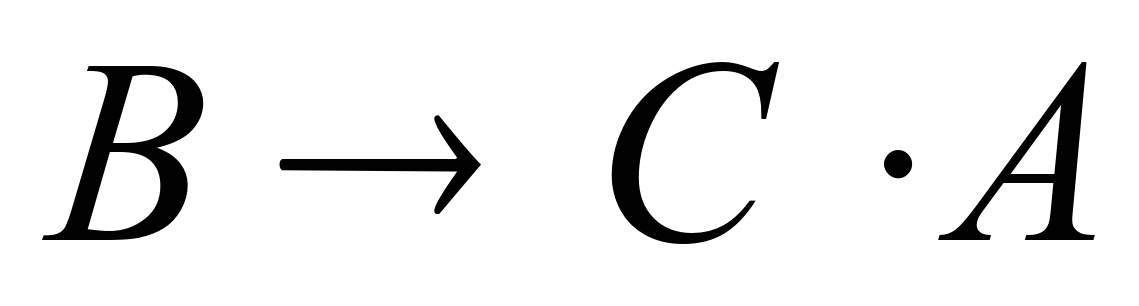
- Запишем произведение указанных функций:
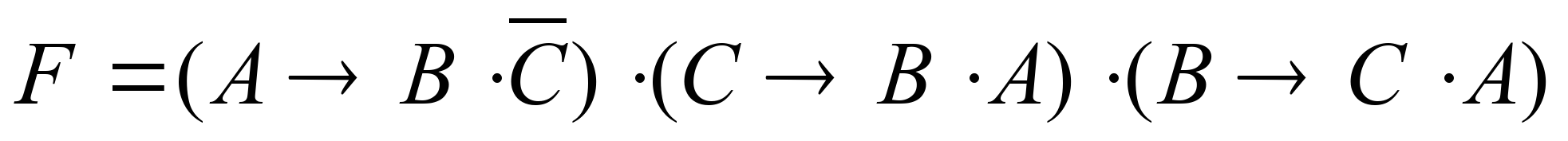
- Упростим формулу (используем законы де Морга, переместительный закон, закон противоречия):
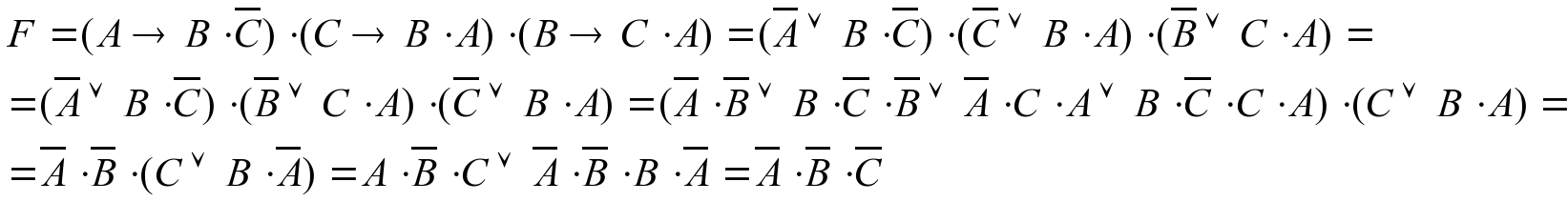
- Приравняем результат единице, т.е. наше выражение должно быть истинным:
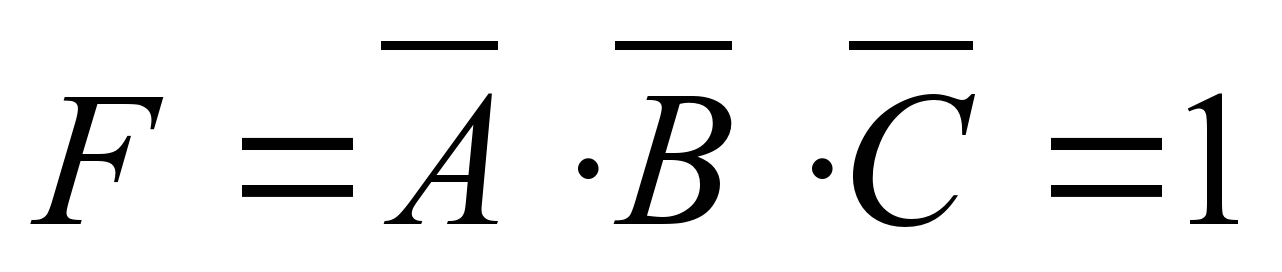
- Проанализируем результат:
Логическое произведение равно 1, если каждый множитель равен 1. Поэтому: 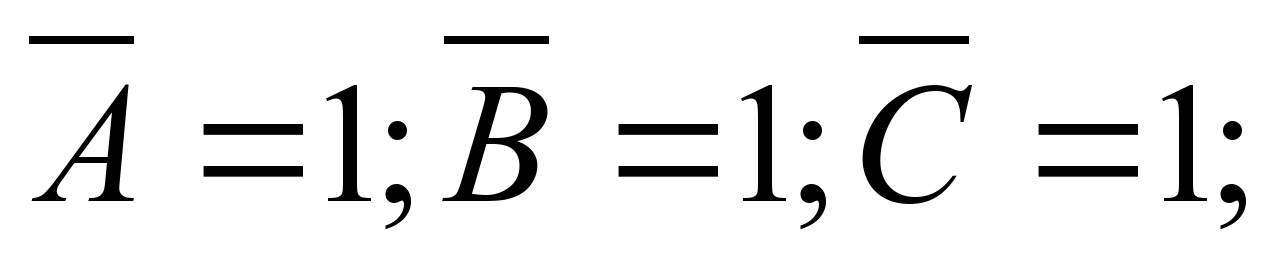 Значит: А=0; В=0; С=0Ответ: погода будет ясная, без дождя, но ветреная. IV. Закрепление изученного материала.Задача 1. В школе-новостройке в каждой из двух аудиторий может находиться либо кабинет информатики, либо кабинет физики. На дверях аудиторий повесили шутливые таблички. На первой повесили табличку «По крайне мере, в одной из этих аудиторий размещается кабинет информатики», а на второй аудитории – табличку с надписью «Кабинет физики находится в другой аудитории». Проверяющему, который пришел в школу, известно только, что надписи на табличках либо обе истинны, либо обе ложны. Помогите проверяющему найти кабинет информатики. Решение. Переведем условие задачи на язык логики высказываний. Так как в каждой из аудиторий может находиться кабинет информатики, то пусть: А – «В первой аудитории находиться кабинет информатики»; В – «Во второй аудитории находится кабинет информатики». Отрицания этих высказываний:
Значит: А=0; В=0; С=0Ответ: погода будет ясная, без дождя, но ветреная. IV. Закрепление изученного материала.Задача 1. В школе-новостройке в каждой из двух аудиторий может находиться либо кабинет информатики, либо кабинет физики. На дверях аудиторий повесили шутливые таблички. На первой повесили табличку «По крайне мере, в одной из этих аудиторий размещается кабинет информатики», а на второй аудитории – табличку с надписью «Кабинет физики находится в другой аудитории». Проверяющему, который пришел в школу, известно только, что надписи на табличках либо обе истинны, либо обе ложны. Помогите проверяющему найти кабинет информатики. Решение. Переведем условие задачи на язык логики высказываний. Так как в каждой из аудиторий может находиться кабинет информатики, то пусть: А – «В первой аудитории находиться кабинет информатики»; В – «Во второй аудитории находится кабинет информатики». Отрицания этих высказываний: 
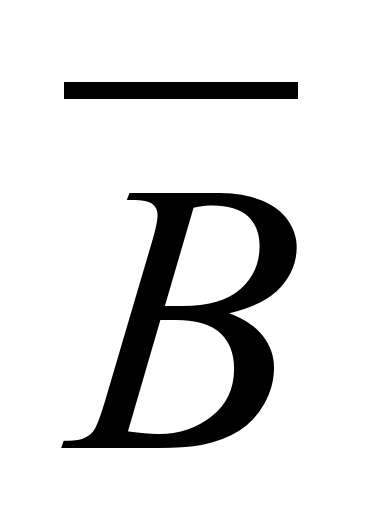 – «Во второй аудитории находиться кабинет физики». Высказывание, содержащееся на табличке на двери первой аудитории, соответствует логическому выражению:
– «Во второй аудитории находиться кабинет физики». Высказывание, содержащееся на табличке на двери первой аудитории, соответствует логическому выражению: 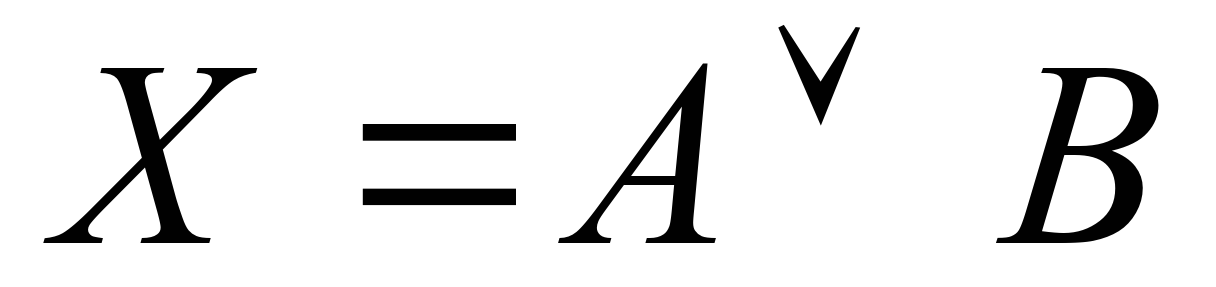 Высказывание, содержащееся на табличке на двери второй аудитории, соответствует логическому выражению:
Высказывание, содержащееся на табличке на двери второй аудитории, соответствует логическому выражению: 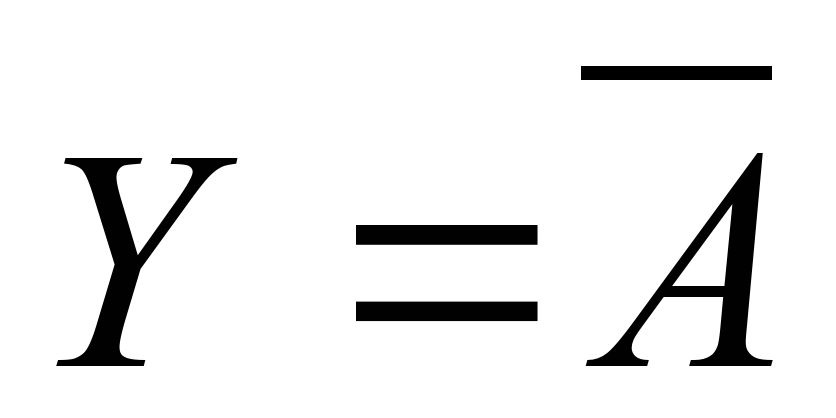 Содержащееся в условии задачи утверждение о том, что надписи на табличках либо одновременно истинные, либо одновременно ложные в соответствии с законом исключенного третьего записывается следующим образом:
Содержащееся в условии задачи утверждение о том, что надписи на табличках либо одновременно истинные, либо одновременно ложные в соответствии с законом исключенного третьего записывается следующим образом: 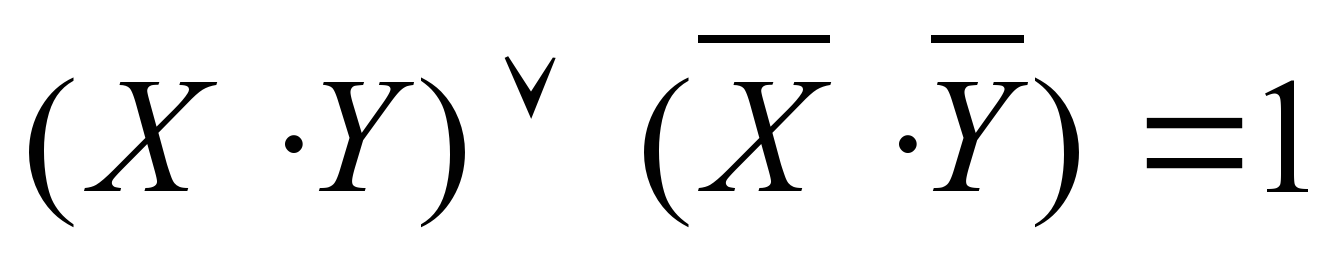 Подставим вместо Х и Y соответствующие формулы:
Подставим вместо Х и Y соответствующие формулы: 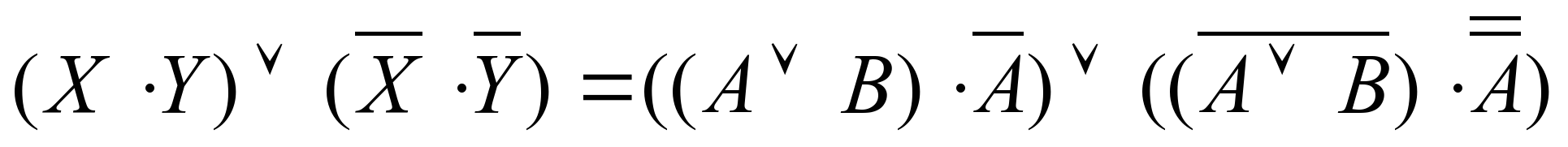 Упростим сначала первое слагаемое. В соответствии с законом дистрибутивности умножения относительно сложения:
Упростим сначала первое слагаемое. В соответствии с законом дистрибутивности умножения относительно сложения: 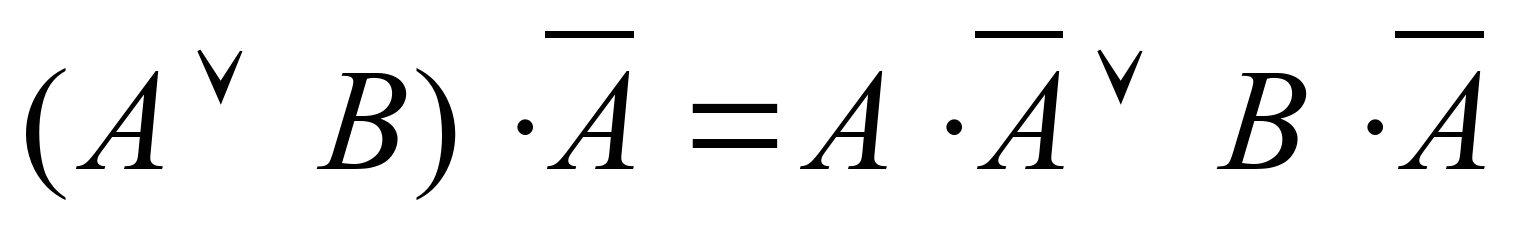 В соответствии с законом непротиворечия:
В соответствии с законом непротиворечия: 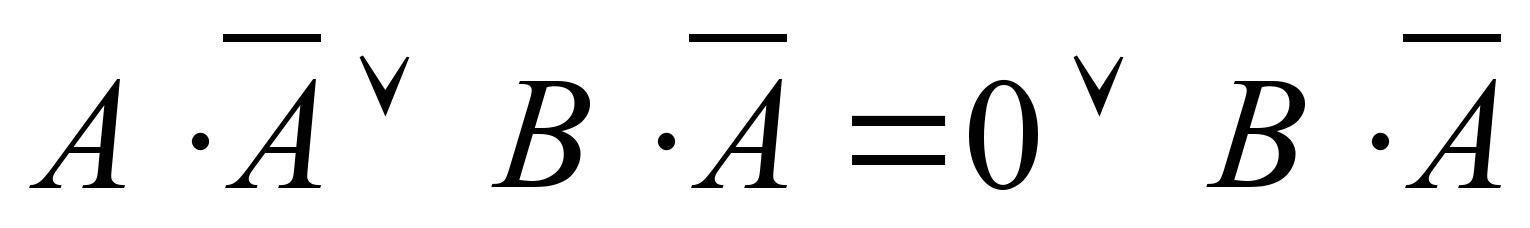 Упростим теперь второе слагаемое. В соответствии с первым законом де Моргана и законом двойного отрицания:
Упростим теперь второе слагаемое. В соответствии с первым законом де Моргана и законом двойного отрицания: 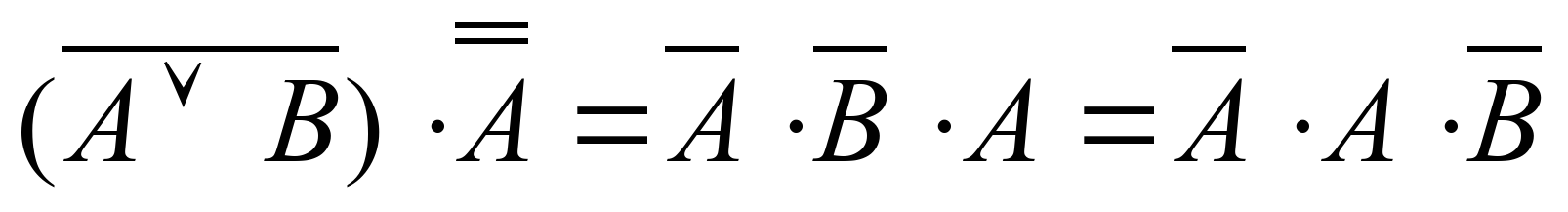 В соответствии с законом непротиворечия:
В соответствии с законом непротиворечия: 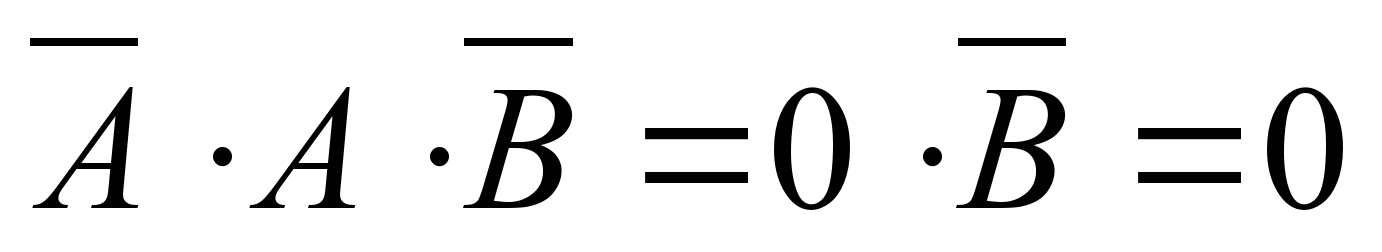 В результате получим:
В результате получим: 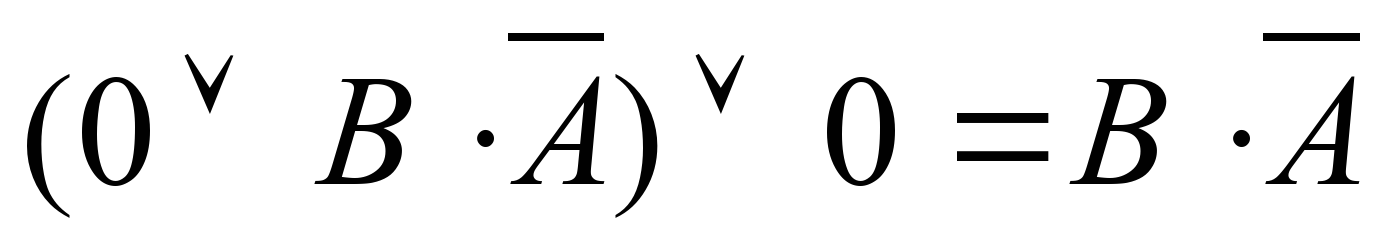 Для того чтобы выполнялось равенство
Для того чтобы выполнялось равенство 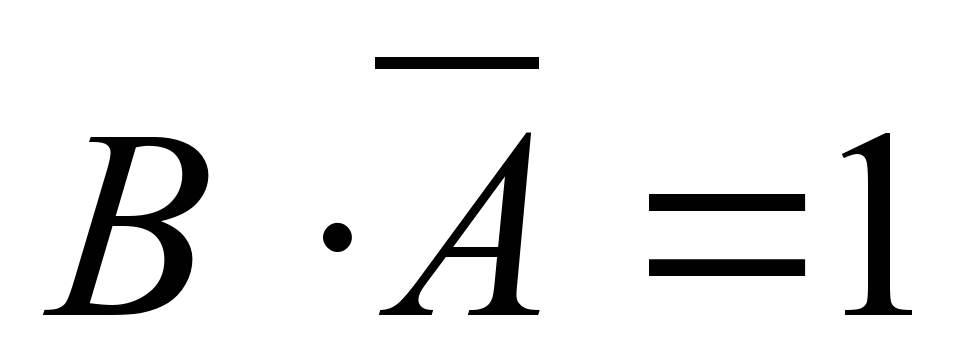 , В и
, В и  должны быть равны 1, то есть соответствующие им высказывания истинны. Ответ. В первой аудитории находится кабинет физики, а во второй — кабинет информатики. Задача 2. На вопрос «Кто из твоих учеников изучал логику?» учитель ответил: «Если логику изучал Андрей, то изучал и Борис. Однако неверно, что если изучал Семен, то изучал и Борис». Кто же изучал логику? Решение. Обозначим буквами высказывания: А — логику изучал Андрей; В — логику изучал Борис; С — логику изучал Семен. Оба высказывания учителя можно записать в виде импликаций: «Если логику изучал Андрей, то изучал и Борис».
должны быть равны 1, то есть соответствующие им высказывания истинны. Ответ. В первой аудитории находится кабинет физики, а во второй — кабинет информатики. Задача 2. На вопрос «Кто из твоих учеников изучал логику?» учитель ответил: «Если логику изучал Андрей, то изучал и Борис. Однако неверно, что если изучал Семен, то изучал и Борис». Кто же изучал логику? Решение. Обозначим буквами высказывания: А — логику изучал Андрей; В — логику изучал Борис; С — логику изучал Семен. Оба высказывания учителя можно записать в виде импликаций: «Если логику изучал Андрей, то изучал и Борис».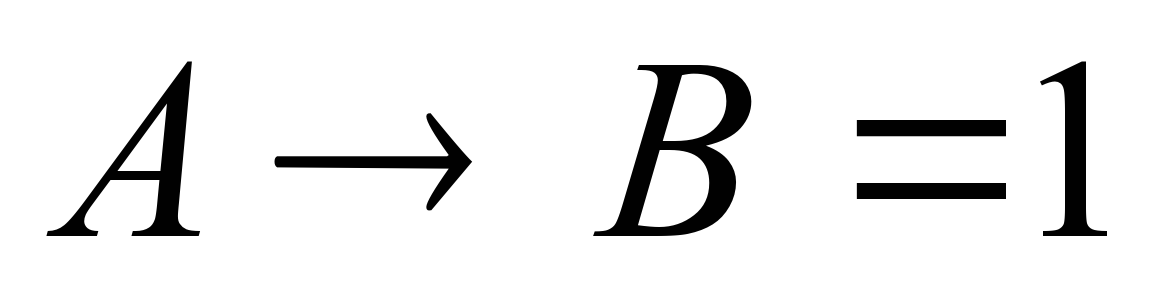 «Неверно, что если изучал Семен, то изучал и Борис».
«Неверно, что если изучал Семен, то изучал и Борис».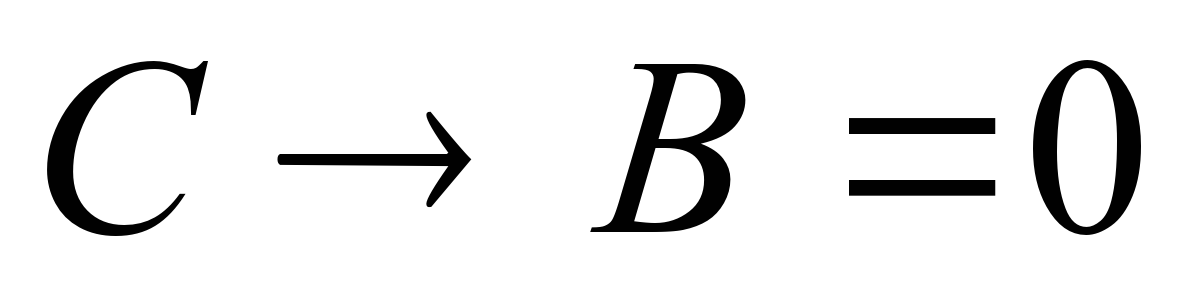 Применим логическое отрицание ко второму высказыванию и составим уравнение с помощью логического умножения:
Применим логическое отрицание ко второму высказыванию и составим уравнение с помощью логического умножения: 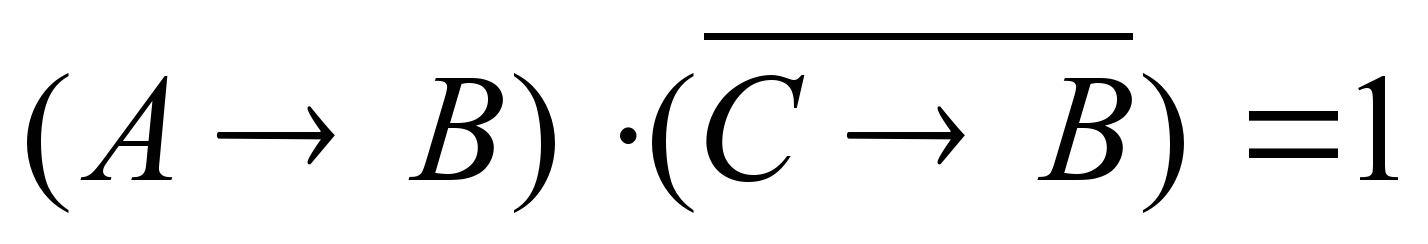 Теперь представляем импликацию через базовые операции и применяем закон де Моргана:
Теперь представляем импликацию через базовые операции и применяем закон де Моргана: 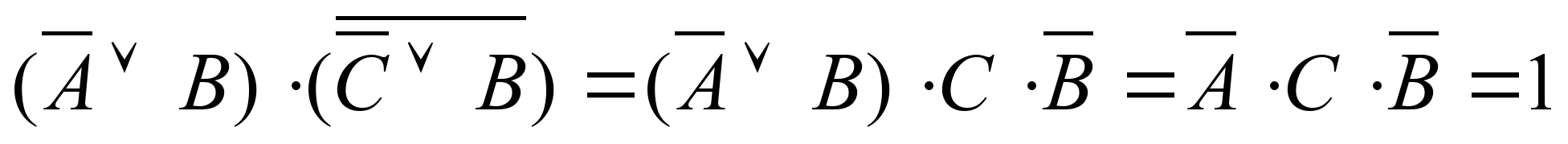 Это уравнение имеет единственное решение:
Это уравнение имеет единственное решение: 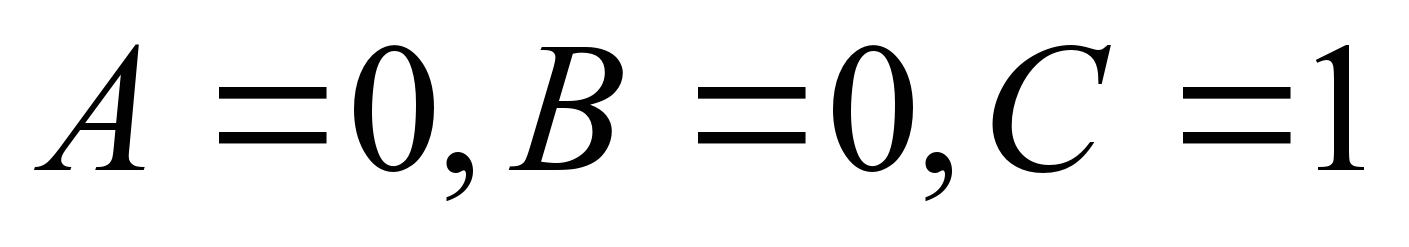 . Ответ: логику изучал только Семен. V. Итог урока. Обобщить пройденный материал, оценить работу активных учеников. VI. Домашнее задание.Задача. Кто из ребят играет в шахматы, если известно, что:
. Ответ: логику изучал только Семен. V. Итог урока. Обобщить пройденный материал, оценить работу активных учеников. VI. Домашнее задание.Задача. Кто из ребят играет в шахматы, если известно, что:
- если играет Андрей или Виктор, то Сергей не играет;
- если Виктор не играет, то играют Сергей и Дмитрий;
- Сергей играет.
Источник: kopilkaurokov.ru