На каждый шкаф расходуется 3,5 м стандартных ДСП, 1 м лицевого стекла и 1 человеко-день трудозатрат. На тумбу -1м ДСП, 2 м стекла и 1 человеко-день трудозатрат.
Прибыль от продажи 1 шкафа составляет 200 у. е., а 1 тумбы -100 у е.
Материальные и трудовые ресурсы ограниченны: в цехе работают 150 рабочих, в день нельзя израсходовать больше 350 м ДСП и более 240 м стекла.
Какое количество шкафов и тумб должен выпускать цех, чтобы сделать прибыль максимальной?
Формализация примера и основные соотношения
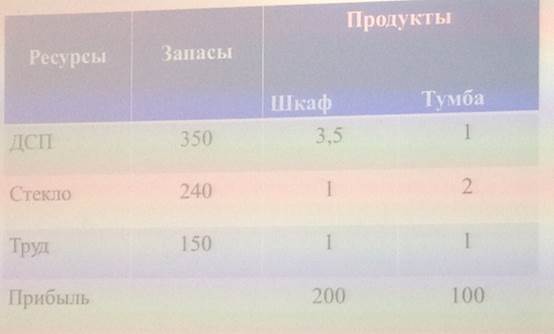
Прежде всего сведем данные — параметры, характеризующие работу цеха, — в следующую таблицу (табл. 1).
Таблица 1 Параметры задачи__________________________________________________________________________________
| Ресурсы | Запасы | Продукты | |
| Шкаф | Тумба | ||
| ДСП | 350 | 3,5 | 1 |
| Стекло | 240 | 1 | 2 |
| Труд | 150 | 1 | 1 |
| Прибыль | 200 | 100 | |
Тумба под TV. Коллекция «Верона»
В колонке «Запасы» запишем предельный расход ресурсов (ДСП, стекла и количества человеко-дней), которые ежедневно может позволить себе начальник цеха.
В колонках «Шкаф» и “Тумба» (продукты, которые может выпускать цех) запишем расход имеющихся ресурсов на единицу продукции (т.е. сколько требуется ДСП, стекла и труда на один шкаф и на одну тумбу).
Наконец, на пересечении колонок «Шкаф» и «Тумба» и строки «Прибыль» запишем величины прибыли от продажи одного шкафа и одной тумбы.
Определим теперь все элементы математической модели данной ситуации (табл. 2):
— целевую функцию и
В данном случае очевидно, что переменные решения (иначе — неизвестные), которые может задавать начальник цеха и от которых зависит целевая функция (прибыль) цеха, — это количество шкафов и тумб, выпускаемых цехом ежедневно.
а) В поле окна «Установить целевую ячейку» (Set target Cell) отметьте ячейку В16 (щелкните сначала по полю окна, а затем по шейке В16);
 |
Рис. 2. Общий вид и работа с окном “Поиск решения”
b) Установите переключатель на отметке «Равной максимальному значению» (Equal to Max);
c) В поле окна «Изменяя ячейки» (By changing Cells) отметьте ячейки В12:С12 (аналогично пункту а).
ТОП- 5 правил как выбрать ТУМБУ под ТВ. Как оформить ТВ зону для современного дизайна интерьер
Добавьте ограничения, щелкая по кнопке «Добавить» (Add).
В появившемся окне, озаглавленном «Добавление ограничения» (рис. 3), щелкните по полю «Ссылка на ячейку», а затем отметьте ячейки В12:С12, выберите знак ограничения, щелкните по правому полю «Ограничение» (Constraints) и введите в него значение 0. Таким образом, вы ввели ограничение X1,X2>0. Вновь щелкните по кнопке «Добавить».
| 31 F |
| Отмена | 1 | Добавить | | 1 |
| Справка |
| Рис. 3. Общий види работа с окном «Добавление ограничения» |
«Значения целевой ячейки не сходятся» или:
«Поиск не может найти решения», или:
«Условия линейной модели не выполняются».
В этом случае следует переставить переключатель в окне «Результаты поиска решения» в положение «Восстановить исходные данные», щелкнуть по кнопке Ok и проверить организацию данных на листе Excel и в установках окна «Поиск решения».
Рассмотрим теперь более сложный пример, включающий большее количество переменных решения. Этот пример позволит продемонстрировать дополнительные технические приемы, полезные при исследовании средних по размеру моделей линейного программирования с помощью MS-Excel.
Источник: all-sci.net
Линейное программирование и метод решения оптимизационной задачи в программе Excel.
цех может выпускать два вида продукции: шкафы и тумбы для телевизора.
на каждый шкаф расходуется 3, 5 м стандартных ДСП, 1 м лицевого стекла и 1 человеко-день трудозатрат.
на тумбу — 1 м ДСП, 2м стекла и 1 человеко-день трудозатрат.
прибыль от продажи 1 шкафа составляет 200 уе, а 1 тумбы — 100 уе.
материальные и трудовые ресурсы ограничены: в цехе работают 150 рабочих, в день нельзя израсходовать больше 350 м ДСП и более 240 м стекла.
какое количество шкафов и тумб должен выпускать цех, чтобы сделать прибыль максимальной?
1. сформулировать цель. цель- получить максимальную цель
2. критерий оптимальности. прибыль у.е. в день z
3. управляемые переменные. х1- количество шкафов, х2 — количество тумб
4. целевая функция 200х1+100х2=z
5. ограничения 3,5х1+х2 меньше 350; х1+2х2 меньше или равно 240; х1+х2 меньше или равно 150; х1 и х2 больше или равно 0
Выработки управляющих воздействий с целью получения оптимального конечного результата.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник: studopedia.ru
Обоснование управленческих решений (Оптимальный план выпуска продукции мебельного цеха) (Отчёт по учебной практике)

Цех собирается выпускать два вида продукции: шкафы и тумбы. На каждый шкаф расходуется 3,5 м стандартных листов ДСП, 1 м листового стекла и 1 человеко-день трудозатрат. На каждую тумбу – ДСП – 1 м, стекла – 2 м и 1 человека-день трудозатрат. Прибыль от продажи 1 шкафа составляет 200 у.е., а тумбы – 100 у.е. В цехе работает 150 человек, запас стекла – 240 м и ДСП – 350 м на день.
Цель выполнения задания
Определить количество шкафов и тумб, которое следует выпускать предприятию для того, чтобы прибыль была максимальной при имеющихся ограниченных ресурсах.
Формализация задачи
Исходные данные: ресурсы, необходимые для изготовления одной единицы продукции каждого вида (листы ДСП, листовое стекло, трудозатраты)
Переменные решения: количество произведенных шкафов(X) и тумб(Y)
Целевая функция: прибыль от продажи произведенных шкафов и тумб
Прибыль = [Кол-во шкафов] * [цена за ед.]+[Кол-во тумб]*[цена за ед.]
P=200*X+100*Y -> max
Ограничения: Расход ДСП и стекла, а также трудозатраты не должны превышать запасов на день и количества человек.
Способ решения и дальнейшее его использование
Данную задачу можно решать двумя способами: методом целочисленного программирования методом линейного программирования. Положительная черта первого способа заключается в получении целочисленной оптимальной программы выпуска изделий, обеспечивающей максимальную прибыль при постоянных заданных количествах ресурсов. Преимущество второго способа состоит в дополнительных возможностях для анализа изменения величины прибыли. Предоставляется возможность проанализировать качественные и количественные изменения ресурсов, а также оценить целесообразности таких изменений. Преимущество линейного программирования в том, что при его использовании для дополнительного анализа можно использовать отчет по устойчивости.
Исходя из содержания поставленной задачи возникает необходимость получения результата в виде целых чисел,
В этом случае имеются два пути: округление результата, полученного способом линейного программирования или решение задачи с целочисленными значениями переменных (целочисленным программированием).
Переход к целочисленному программированию сводится к вводу для переменных решения дополнительного ограничения со значением “цел.”.
Следует иметь в виду, что добавление этого ограничения исключает использование эффективных методов решения задач линейного программирования. Результаты решения задач при использовании целочисленных переменных более сложны для анализа, а алгоритмы менее универсальны и эффективны. Это значит, что вероятность нахождения экстремума целевой функции снижается.
Используется надстройка Excel “Поиск решения” как основное программное средство для выполнения задания.
Описание результатов, используемых при анализе
В результате решения задачи способом линейного программирования получены следующие результаты
Оптимальное количество производства шкафов = 80
Оптимальное количество производства тумб = 70
При этом выполнены все ограничения, и максимальная прибыль 23000 руб
Фактический расход ресурсов
Источник: vunivere.ru