Математическая статистика — область современной математики, основанная на теории вероятностей и занятая поиском законов изменения и способов измерения случайных величин, обоснованием методов расчетов, производимых с такими величинами.
Математическая статистика возникла (XVII в) и развивалась параллельно с теорией вероятностей. Дальнейшее развитие математической статистики (вторая половина XIX — начало XX в) обязано, в первую очередь, П.Л. Чебышеву, А.А. Маркову, А.М. Ляпунову, а также К. Гауссу, А. Кетле, Ф. Гальтону, К. Пирсону и др.
В XX в. Наиболее существенный вклад в математическую статистику был сделан советскими математиками (В.И. Романовский, Е.Е. Слуцкий, А.Н. Колмогоров, Н.В. Смирнов).
Математическая статистика применяется не только в экономических науках, но и в педагогике, психологии, а также в других областях практической науки. В нашей повседневной жизни мы, сами о том не догадываясь, постоянно занимаемся статистикой. Хотим ли мы спланировать бюджет, рассчитать потребление бензина автомашиной, оценить усилия, которые потребуются для усвоения какого-то курса, с учетом полученных до сих пор отметок, предусмотреть вероятность хорошей и плохой погоды по метеорологической сводке или вообще оценить, как повлияет то или иное событие на наше личное или совместное будущее, — нам постоянно приходится отбирать, классифицировать и упорядочивать информацию, связывать ее с другими данными так, чтобы можно было сделать выводы, позволяющие принять верное решение.
ЧВК Редан #обществознание #огэ #shorts
Рассмотрим основные этапы простейшей статистической обработки данных:
1) сначала данные измерений упорядочивают и группируют;
2) составляют паспорт данных измерения, который состоит из основных числовых характеристик полученной информации;
3) затем составляют таблицы распределения данных;
4) с помощью таблиц распределения строят графики распределения данных в виде многоугольника распределения, гистограммы распределения или круговой диаграммы.
Введем основные понятия, необходимые нам для обработки ряда данных.
Каждое число, встретившееся в конкретном измерении, называют вариантой измерения.
Если среди всех данных конкретного измерения одна из вариант встретилась k раз, то число k называют кратностью этой варианты.
Если записать все варианты в порядке возрастания, начиная с наименьшей, то получим сгруппированный ряд данных.
Среднюю варианту в сгруппированном ряду данных называют медианой.
Модой называют количественное значение исследуемого признака, наиболее часто встречающееся в выборке.
Объем измерения – это количество вариант данного ряда.
Частное от деления суммы всех вариант на объем измерения называется средним (средним арифметическим).
Размах измерения –это разность между наибольшей и наименьшей вариантой.
Если кратность варианты разделить на объем измерения, то получим частоту варианты.
А если частоту варианты умножить на 100%, то получим частоту варианты в процентах.
ЕГЭ 2020 (база) вариант 7
Рассмотрим пример 1.
При изучении учебной нагрузки выделили группу из 12 учащихся одного класса. Их попросили в определенный день отметить время (в минутах), затраченное на выполнение домашнего задания по математике.
Получили следующие результаты: 23,18,25,20,25,25,32,37,34,26,34,25.
Это общий ряд данных, с ним работать неудобно, поэтому составим упорядоченный ряд данных: 18,20,23,25,25,25,25,26,32,34,34,37.
Определим основные характеристики:
Таблица распределения данных: частот и частот в% (сводная).
| Варианта | 18 | 20 | 23 | 25 | 26 | 32 | 34 | 37 |
| Кратность | 1 | 1 | 1 | 4 | 1 | 1 | 2 | 1 |
| Частота | 0,08 | 0,08 | 0,08 | 0,33 | 0,08 | 0,08 | 0,17 | 0,08 |
| Частота,% | 8 | 8 | 8 | 33 | 8 | 8 | 17 | 8 |
С помощью этой таблицы мы можем построить различные графики:
— график распределения данных (график кратностей);
— график распределения частот в %.
Способы графического представления ряда данных:
-гистограмма (столбчатая диаграмма);
— многоугольник распределения (полигон).
1)Построим гистограмму распределения данных.
2)построим круговую диаграмму распределения частот в %.
3,7◦∙33=122,1◦ — это 33%
3,7◦∙17= 62,9◦- это 17%.
Пример 2. У 25 девятиклассников спросили, сколько часов в день в среднем они смотрят телевизор. Вот что получили:
| Часов | 0 | 1 | 2 | 3 | 4 |
| Человек | 1 | 9 | 10 | 4 | 1 |
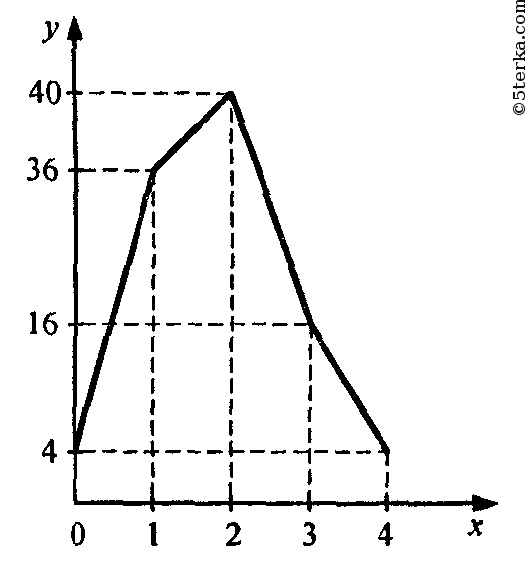
Определите: основные характеристики данного ряда, постройте полигон распределения процентных частот.
Объем=25, мода=2, медиана= 2, размах=3, среднее=45:25=1,8,
Таблица частот в %:
| Часов | 0 | 1 | 2 | 3 | 4 |
| Человек | 1 | 9 | 10 | 4 | 1 |
| Частота, % | 4 | 36 | 40 | 16 | 4 |
По горизонтали – часы, по вертикали – частоты, точки соединить.
В некоторых измерениях в качестве варианты используют не число, а интервал (промежуток), например, от 1 до 3 часов, от 3 до 5 часов.
Итак, математическая обработка информации, собранной в результате проведенного измерения, позволяет упорядочить данные, чтобы они занимали меньше места, представить наглядно результаты измерения, выяснить основные характеристики ряда данных.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник: studopedia.ru
19.9. У 25 девятиклассников спросили, сколько в среднем часов в день они смотрят телевизор. Вот что получилось: Определите: а) размах; б) моду; в) среднее значение. Постройте многоугольник процентных частот; укажите на нем данные, полученные в заданиях а)
Определите: а) размах; б) моду; в) среднее значение. Постройте многоугольник процентных частот; укажите на нем данные, полученные в заданиях а) — в).
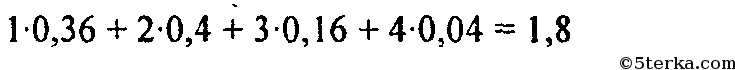
Источник:

Решебник по алгебре за 9 класс (А.Г. Мордкович, Л.А. Александрова, Т.Н. Мишустина и др., 2010 год),
задача №19.9.
к главе «§19. Статистика — дизайн информации».
Источник: 5terka.com
Упр.19.9 ГДЗ Мордкович 9 класс (Алгебра)
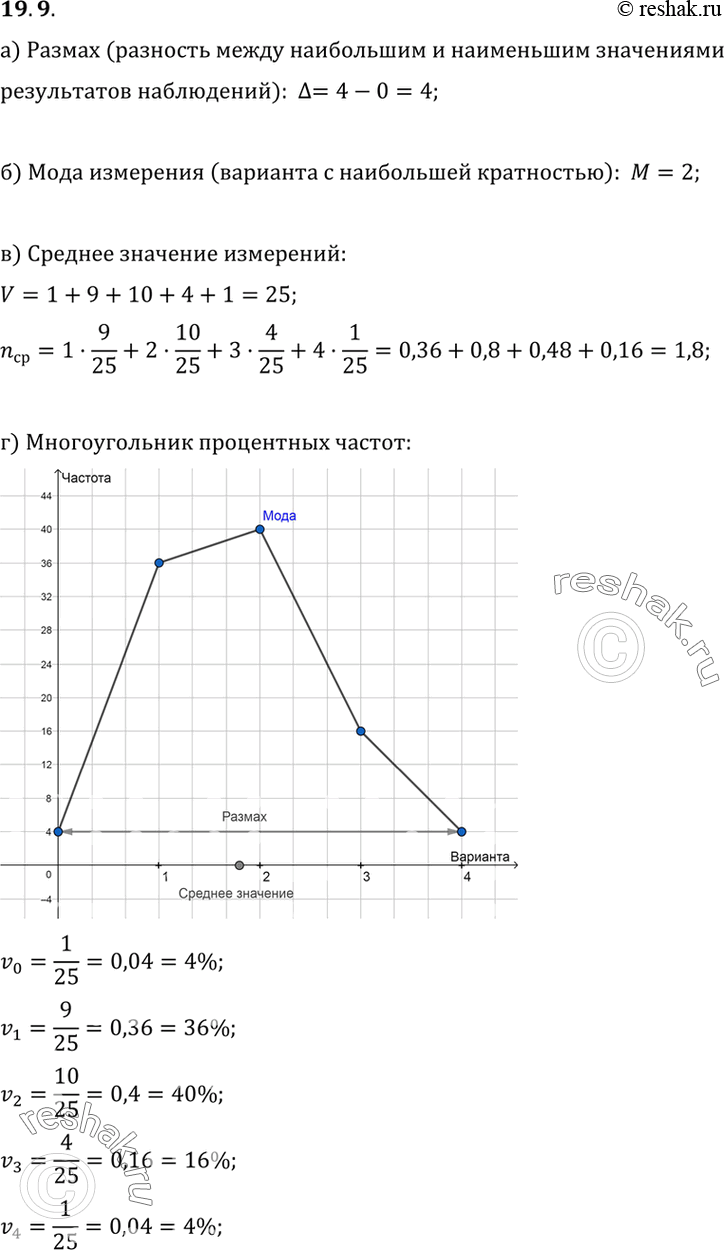
19.9. У 25 девятиклассников спросили, сколько в среднем часов в день они смотрят телевизор. Вот что получилось:
ТВ, ч в день 0 1 2 3 4
Число школьников 1 9 10 4 1
Определите: а) размах; б) моду; в) среднее значение. Постройте многоугольник процентных частот; укажите на нем данные, полученные в заданиях а) — в).
*Цитирирование задания со ссылкой на учебник производится исключительно в учебных целях для лучшего понимания разбора решения задания.
Популярные решебники 9 класс Все решебники
Юдовская, Баранов, Ванюшкина
Рудзитис, Фельдман
Боголюбов, Лазебникова, Матвеев
Михеева, Афанасьева
Погорелов 7-9 класс
Ладыженская
Ладыженская, Тростенцова

§18. Комбинаторные за.
§19. Статистика — диз.
Главная задача сайта: помогать школьникам и родителям в решении домашнего задания. Кроме того, весь материал совершенствуется, добавляются новые сборники решений.
Источник: reshak.ru