Найди верный ответ на вопрос ✅ «В лотерее разыгрывалось 5 автомобилей, 12 мотоциклов, 25 телевизоров. Всего было выпущено 4000 лотерейных билетов. Какова вероятность: 1) . » по предмету Математика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Новые вопросы по математике
2 тыс=. Дес 2 дес. тыс.=тысяч. 5 сот тысяч=дес. тыс 3 дес. тыс=сот тысяч 10 дес=ед 20 дес. тыс=сот тысяч
В треугольнике авс сторона ав=корень из 43, вс=корень из 59, ас=4. Найдите величину наибольшего угла
Сколько существует различных расположений 15 монеток, в которых нет 2 подряд идущих орлов?
Стороны треугольника равны 3/8 м, 1/2 м, 5/6 м. Найти периметр.
Всем привет. В магазине в 1 день продали 35%, во 2 — 28%всеховощей, А в 3 — оставшиеся 333 кг. Сколько кг овощейбыло в магазине первоначально?
Главная » Математика » В лотерее разыгрывалось 5 автомобилей, 12 мотоциклов, 25 телевизоров. Всего было выпущено 4000 лотерейных билетов. Какова вероятность: 1) выиграть мотоцикл2) выиграть какой-либо приз3) не выграть никакого приза
Источник: urokam.net
Кое-что из прошлого теории вероятности.
Еще первобытный вождь понимал, что у десятка охотников вероятность поразить копьем зубра гораздо больше, чем у одного. Поэтому и охотились только коллективно.
Неосновательно было бы думать, что такие древние полководцы, как Александр Македонский или Дмитрий Донской, готовясь к сражению, уповали только на доблесть и искусство воинов.
Несомненно, они на основании наблюдений и опыта военного руководства умели как-то оценить вероятность своего возращения со щитом или на щите, знали, когда принимать бой, когда уклониться от него. Они не были рабами случая, но вместе с тем они были еще очень далеки от теории вероятностей.
Позднее, с опытом, человек все чаще стал взвешивать случайные события, классифицировать их исходы как невозможные, возможные и достоверные. Он заметил, что случайностями не так уж редко управляют объективные закономерности. Вот простейший опыт – подбрасывают монету. Выпадение орла или решки, конечно, чисто случайное явление. Но при многократном подбрасывании обычной монеты можно заметить, что появление решки происходит примерно в половине случаев.
Кто и когда впервые проделал опыт с монетой, неизвестно. Французский естествоиспытатель Ж.Л.Л.Бюффон (1707 – 1788) в 18 столетии 4040 раз подбрасывал монету – решка выпала 2048 раз. Математик К.Пирсон в начале двадцатого столетия подбрасывал ее 24 000 раз – решка выпала 12 012 раз. Лет 40 назад американские экспериментаторы повторили опыт. При 10 000 подбрасываний решка выпала 4 979 раз.
Значит, результаты бросаний монеты, хотя каждое из них и является случайным событием, при неоднократном повторении подвластны объективному закону.
Наиболее интересные задачи теории вероятности возникли в области азартных игр. Этому, по-видимому, способствовало наличие таких “наглядных пособий”, как монета или игральная кость.
К азартным играм относили бросание шестигранных игральных костей. Слово “азар” по-арабски означает “трудный”. Так, арабы называли азартной игрой комбинацию очков, которая при бросании нескольких костей могла появиться лишь единственным способом. Например, при бросании двух костей трудным (“азар”) считалось появление в сумме двух или двенадцати очков.
Впервые основы теории вероятностей были изложены последовательно французским математиком П.Лапласом (1749-1827) в книге “Аналитическая теория вероятностей”.
В предисловии автор писал: “Замечательно, что наука, которая началась с рассмотрения азартных игр, обещает стать наиболее важным объектом человеческого знания… Ведь по большей части важнейшие жизненные вопросы являются на самом деле лишь задачами теории вероятностей”.
П.Лаплас не мог предусмотреть, что пройдет несколько десятилетий и интерес к теории вероятностей снизится. А так на деле и случилось. Во второй половине XIX века и в начале XX века некоторые математики перестали интересоваться теорией вероятностей как математической дисциплиной.
К счастью последние годы теория вероятностей вернулась в школьную программу, медленными, но уверенными шагами. Вот и наша задача – научиться решать такие жизненные задачи с помощью теории вероятностей.
Вернёмся к эксперименту с подбрасыванием монеты. Многие ученые проводили его и получали различные, но близкие значения.
Говоря о том, что монета однородна и имеет правильную геометрическую форму, можно сделать вывод, что случаи выпадения орла или решки имеют одинаковые шансы. Такие события называют равновозможными.
Найдём вероятность события выпадения орла.
Всего при подбрасывании монеты могут быть 2 равновозможных исхода: выпадет орёл или решка. Для нас благоприятным событием является первое. Среди всех возможных оно встречается 1 раз. Тогда получаем, что относительная вероятность выпадения орла равна: .
Определение:
Если все исходы какого-либо испытания равновозможны, то вероятность события в этом испытании равна отношению числа благоприятных для него исходов к числу всех равновозможных исходов.
Такой способ отыскания относительной вероятности называется классическим. Но полученное значение вероятности совсем не означает, что если подбросить монету два раза, то один раз выпадет орёл.
Вывод: статистический подход предполагает проведение испытаний, а классический — нет.
Чтобы вычислить вероятность события классическим способом необходимо только правильно определить количество всех равновозможных исходов, а также число благоприятных для этого события исходов.
Пример. Студент не выучил 3 билета из тридцати. Какова вероятность того, что он сдаст экзамен?
Пусть А — событие, при котором сдан экзамен. Студент может вытянуть на экзамене любой из тридцати билетов, то есть n=30.
Благоприятным исход m=27 — число билетов, которые он выучил. Получим:
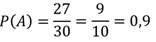
Рассмотрим следующие примеры:
Пример 1. Пусть на стол бросают монету. В результате обязательно произойдет одно из двух событий (либо “выпала решка”, либо “выпал орел”)
Событие А: “Выпала решка”
Событие В: “Выпал орел”
Так как предполагается, что монета не изогнута, то события А и В в нашем примере равновозможные и одно из них обязательно произойдет. Тогда вероятность события определяется следующим образом: Р(А) = , где n – число всех равновозможных случаев, m – число случаев, благоприятствующих событию А. Тогда Р(А) = и Р(В) = .
Пример 2. Пусть на стол бросают игральный кубик.
Возможны 6 случаев: выпадение 1, 2, 3, 4, 5, 6 очков. Эти случаи равновозможные.
Событие А: “выпадение 3 очков”, тогда Р(А) = .
Пример 3. Двое играют в эту игру. Они бросают два кубика. Первый получает очко, если выпадет сумма 8. Второй получает очко, если выпадет сумма 9. Справедлива ли эта игра?
Событие А: “при бросании двух кубиков выпало 8 очков”
Событие В: “при бросании двух кубиков выпало 9 очков”
При бросании двух кубиков могут получиться следующие равновозможные результаты:
| I II | I II | I II | I II | I II | I II |
| 1 1 1 2 1 3 1 4 1 5 1 6 | 2 1 2 2 2 3 2 4 2 5 2 6 | 3 1 3 2 3 3 3 4 3 5 3 6 | 4 1 4 2 4 3 4 4 4 5 4 6 | 5 1 5 2 5 3 5 4 5 5 5 6 | 6 1 6 2 6 3 6 4 6 5 6 6 |
n = 36 – число всех равновозможных случаев;
m = 5 – число случаев благоприятствующих событию А;
к = 4 – число случаев благоприятствующих событию В.
Так как 8 очков выпадает чаще, чем 9 очков, то данная игра не справедлива.
Задание: Выполнить самостоятельную работу (прилагается)
Самостоятельная работа » Вероятность случайного события»
Вариант 1.
1. Охарактеризуйте событие, о котором идет речь, как достоверное, невозможное или случайное:
а) На каждом уроке математики ученики решали математические задачи.
б) На зимней олимпиаде в Сочи все призовые места займут российские спортсмены.
в) В каждом месяце дней не меньше, чем 28.
г) В написании выбранного слова нет согласных букв.
д) Из интервала (-1;1) наугад взяли какое-то число. Оно оказалось натуральным.
2. В фирме такси в данный момент свободно 15 машин: 2 красных, 9 желтых и 4 зеленых. По вызову выехала одна из машин, случайно оказавшихся ближе всего к заказчице. Найдите вероятность того, что к ней приедет желтое такси.
3. Ученика попросили назвать число от 1 до 100. Какова вероятность того, что он назовет число кратное 5?
4. Женя, Лена, Маша, Аня и Коля бросили жребий – кому идти в магазин. Найдите вероятность того, что в магазин надо будет идти Ане.
5. Бросают игральный кубик. Найдите вероятность того, что выпадет число, меньшее 4 очков.
6. В коробке лежат 10 карточек, пронумерованных числами от 1 до 10. Какова вероятность того, что на наугад вынутой карточке будет записано:
а) Чётное число б) Число, кратное 3
7. В коробке лежат 18 зелёных и 12 голубых шариков. Какова вероятность того, что выбранный наугад шарик окажется зелёным.
8. В лотерее разыгрывалось 5 телевизоров, 25 магнитофонов, 30 фотоаппаратов. Всего было выпущено 3000 лотерейных билетов. Какова вероятность выиграть:
а) выиграть фотоаппарат б) выиграть какой-нибудь приз
9. В чемпионате по гимнастике участвуют 80 спортсменок: 23 из Аргентины, 29 из Бразилии, остальные — из Парагвая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Парагвая.
10. На тарелке 12 пирожков: 5 с мясом, 4 с капустой и 3 с вишней. Наташа наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
11. Миша с папой решили покататься на колесе обозрения. Всего на колесе двадцать четыре кабинки, из них 5 — синие, 7 — зеленые, остальные — красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Миша прокатится в красной кабинке.
12. У бабушки 20 чашек: 5 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
13. В среднем из каждых 80 поступивших в продажу аккумуляторов 76 аккумуляторов заряжены. Найдите вероятность того, что купленный аккумулятор не заряжен.
14. Для экзамена подготовили билеты с номерами от 1 до 50. Какова вероятность того, что наугад взятый учеником билет имеет однозначный номер?
15. Приведите примеры: а) достоверного, б) возможного и в) случайного события.
Источник: poisk-ru.ru
В лотерее разыгрывалось 10 телевизоров, 15 видеокамер, 20 фотоаппаратов. Всего было выпущено 1000 лотерейных билетов.
Какова вероятность: 1) Выиграть видеокамеру; 2)Выиграть какой-нибудь приз; 3) Не выиграть никакого приза?
Ответы
Будь первым, кто ответит на вопрос
Как добавить хороший ответ?
Что необходимо делать:
- Написать правильный и достоверный ответ;
- Отвечать подробно и ясно, чтобы ответ принес наибольшую пользу;
- Писать грамотно, поскольку ответы без грамматических, орфографических и пунктуационных ошибок лучше воспринимаются.
Что делать не стоит:
- Списывать или копировать что-либо. Высоко ценятся ваши личные, уникальные ответы;
- Писать не по сути. «Я не знаю». «Думай сам». «Это же так просто» — подобные выражения не приносят пользы;
- Писать ответ ПРОПИСНЫМИ БУКВАМИ;
- Материться. Это невежливо и неэтично по отношению к другим пользователям.
Пример вопроса
Русский язык
7 минут назад
Какой синоним к слову «Мореплаватель»?
Пожаловаться
Хороший ответ
Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Источник: uchi.ru