В магазине 10 телевизоров, из которых 2 неисправных. Найти вероятность того, что среди наудачу взятых 3-х телевизоров будет хотя бы один неисправный.
(Ответ: 0,53)
Нужны сами действияметоды решения данной задачи.
Заранее спасибо.
Лучший ответ
Вероятность взять три ИСПРАВНЫХ телевизора равна 8/10*7/9*6/8=0,4667.
Поэтому вероятность ПРОТИВОПОЛОЖНОГО события, а именно того, что ХОТЯ БЫ один телевизор будет неисправен, равна 1-0,4667=0,5333.
Вот и все действия, вместе с методами. Можно рассчитать по другому, с использованием методов комбинаторики. Ответ от этого не изменится.
Остальные ответы
Похожие вопросы
Источник: otvet.mail.ru
Противоположные события. Полная группа событий
ТЕОРЕМА 2. Сумма вероятностей событий, образующих полную группу, равна единице:
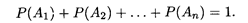
Оцените создание мыла от 1 до 10 ) Как вы думаете, сколько мне лет? Пишите в комменты
Пример 2. На складе готовой продукции находятся изделия, среди которых 5% нестандартных. Найти вероятность того, что при выдаче изделия со склада оно будет стандартным.
Решение. Вероятность получения нестандартного изделия равна 0,05; события выдачи стандартного и нестандартного изделия образуют полную группу. Следовательно, сумма их вероятностей равна единице, и тогда искомая вероятность равна 0,95.
Определение 2. Два единственно возможных события, образующих полную группу, называются противоположными.
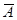
Если событие обозначено через А, то противоположное ему событие обозначается через . Из теоремы 17.2 следует, что
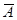
Например, если при стрельбе по мишени попадание — это событие А, то событие — это промах; сумма их вероятностей равна единице — при выстреле обязательно будет либо попадание, либо промах. То же самое и при подбрасывании монеты: обязательно выпадет либо орел, либо решка.
Пример 3. В магазине имеется 10 телевизоров, из которых 2 неисправных. Найти вероятность того, что среди наугад взятых 3-х телевизоров будет хотя бы один неисправный.
Решение. События «среди взятых телевизоров нет ни одного неисправного» и «есть хотя бы один неисправный» — противоположные. Первое из них обозначим через А, а второе — через 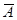. Общее число способов, которыми можно взять 3 изделия из десяти, равно C
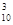. Число исправных телевизоров равно 8, число способов выборки из них трех изделий равно C
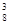, так что вероятность Р(А) = C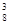/С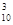. Искомая вероятность определяется из формулы (17.4):
Телевизоры LG. Новая линейка UQ76003LD — 43, 50, 55 и 65 дюймов.
Источник: studopedia.su
В магазине имеется 10 телевизоров из которых 2 неисправных
nbspnbspnbspnbspnbspnbspnbsp На место командира есть три кандидата а1, а2, а3; на место инженера – четыре кандидата в1, в2, в3, в4; на место врача – два кандидата с1, с2. Проведенная проверка показала психологическую несовместимость командира а2 с инженерами в3, в4 и с врачом с2; а также инженера в2 с врачом с2. будем для простоты считать, что без учета несовместимости, все варианты составления команды равновозможны. Какова вероятность того, что будет составлен экипаж, все члены которого психологически совместимы друг с другом?
nbspnbspnbspnbspnbspnbspnbsp Представим все варианты состава, при котором члены экипажа совместимы друг с другом, в виде «дерева». Число ветвей этого дерева, т.е. исходов, благоприятствующих событию А, равно 16, а общее число возможных комбинаций n = 4•3•2 = 24.
nbspnbspnbspnbspnbspnbspnbsp Пример. Какова вероятность того, что при случайном расположении в ряд кубиков, на которых написаны буквы A,A,A,Н,Н,С получится слово «АНАНАС».
nbspnbspnbspАНАНАС». Буква А используется три раза, Н – два и С – один раз. Следовательно, n=P6(3,2,1). Событию A благоприятствует один случай:
nbspnbspnbspnbspnbspnbspnbsp Решение. Пусть событие A – 3 извлеченные наудачу детали окрашены. Общее число случаев выбора 3 деталей из 15 равно n=C15 3 , так как комбинации из 15 деталей по 3 представляют собой сочетания, ибо отличаются лишь составом деталей. Аналогично, число случаев, благоприятствующих событию A, равно C10 3 . Следовательно,
nbspnbspnbspnbspnbspnbspnbsp Решение. Пусть событие A – все пассажиры выйдут на одном этаже. Общее число способов выхода пассажиров из лифта представляют собой размещения с повторениями из 8 элементов (этажей) по 4. Их число равно . Число случаев, благоприятствующих событию A, m=8 (все пассажиры выйдут или на 2-м этаже, или на 3-м,…, или на 9-м этаже). Таким образом,
nbspnbspnbspnbspnbspnbspnbsp Решение. Пусть событие A – среди взятых телевизоров есть хотя бы один неисправный. Общее число способов, которыми можно выбрать 3 телевизора из десяти, n=C10 3 . Всего 2 неисправных телевизора, «хотя бы один неисправный» означает, что неисправных телевизоров либо один, либо два. Событию A благоприятствуют случаи, когда из взятых 3 телевизоров будет либо один неисправный (и два исправных), либо два неисправных (и один исправный); их число . Поэтому
nbspnbspnbspnbspnbspnbspnbsp Решение. Событие А состоит в том, что среди купленных акций две окажутся акциями банкротов. Общее число элементарных исходов испытания равно числу способов, которыми можно выбрать шесть АО из двадцати, т.е. C20 6 : Число благоприятствующих исходов определяется по правилу произведения как
Согласно классическому определению вероятности имеем:
nbspnbspnbspnbspnbspnbspnbsp Решение. Пусть событие A – среди взятых телевизоров есть хотя бы один неисправный. Общее число способов, которыми можно выбрать 3 телевизора из десяти, n=C10 3 . Всего 2 неисправных телевизора, «хотя бы один неисправный» означает, что неисправных телевизоров либо один, либо два. Событию A благоприятствуют случаи, когда из взятых 3 телевизоров будет либо один неисправный (и два исправных), либо два неисправных (и один исправный); их число . Поэтому
nbspnbspnbsp хотя бы один?
nbspnbspnbspnbspnbspnbspnbsp Пример. В магазин поступило 20 новых цветных телевизоров, среди которых 6 имеют скрытый дефект. Наудачу отбирается один телевизор для проверки. Какова вероятность, что он не имеет скрытых дефектов?
nbspnbspnbspnbspnbspnbspnbsp Пример. Какова вероятность того, что при случайном расположении в ряд кубиков, на которых написаны буквы получится слово ?
nbspnbspnbspАЛГОРИТМ». Различные комбинации восьми букв из имеющихся восьми представляют собой перестановки, так как отличаются только порядком следования букв, т.е. общее число случаев n=P(8). Благоприятствует событию A m=1 случай. Поэтому
nbspnbspnbspnbspnbspnbspnbsp Решение. Событие B – «студент угадает расписание». Число всевозможных исходов данного испытания
, из которых лишь один благоприятствует событию B, т.е. m=1. В соответствии с классическим определением вероятности, получаем
nbspnbspnbsp один белый и один черный шар?
nbspnbspnbspnbspnbspnbspnbsp Число всех элементарных исходов испытания равно числу сочетаний из 10 по 2:
nbspnbspnbspnbspnbspnbspnbsp Пример. Среди кандидатов в студенческий совет факультета 4 первокурсника и 5 второкурсников. Из этого состава наудачу выбирают пять человек на предстоящую конференцию. Найти вероятность того, что два первокурсники попадут на предстоящую конференцию (событие )?
nbspnbspnbspnbspnbspnbspnbsp Пример. Из 30 студентов 10 имеют спортивные разряды. Какова вероятность того, что выбранные наудачу 3 студента – разрядники?
nbspnbspnbspnbspnbspnbspnbsp Пример. (геометрическое определение). Известно, что троллейбус № 20 ходит с интервалом 15 минут. Какова вероятность того, что, придя на остановку, вы будете ожидать троллейбус не менее 5 и не более 12 минут?
nbspnbspnbspnbspnbspnbspnbsp Пример. На прямолинейном участке газопровода длиной 80 км произошел разрыв. Какова вероятность того, что разрыв удален от обоих концов участка на расстояние, большее 30 км?
nbspnbspnbsphttps://openedo.mrsu.ru/catalog/Estestvennie/2014/kulashova_matstat/lekcii/razdel7/2.html» target=»_blank»]openedo.mrsu.ru[/mask_link]