0) Вероятность попадания в мишень при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена: а) 75 раз; б) от 75 до 84 раз; в) менее 75 раз; г) не менее 70 раз.
1) Монету бросают 6 раз. найти вероятность того, что: а) герб выпадает три раза; б) герб выпадает один раз; в) герб выпадет не менее двух раз.
2) Стрелок четыре раза стреляет по мишени. Считая, что вероятность попадания при одном выстреле не зависит от результатов предшествующих выстрелов равна 0,8, найти вероятность того, что стрелок попал в мишень: а) два раза; б) не более трёх раз; в) хотя бы один раз; г) один раз.
3) в среднем 10% автомобилей, производимых заводом, имеют брак. Для контроля из партии автомобилей взяли 5 машин. Найти вероятность того, что среди них будет: а) 3 машины без брака; б) не более 3 машин без брака.
4) Вероятность того, что телевизор имеет скрытые дефекты, равна 0,2. В отдел магазина поступило 20 телевизоров. Что вероятнее: что в этой партии имеется два телевизора со скрытыми дефектами или три?
Задача по теории вероятностей из ЕГЭ и ОГЭ по математике
5) Устройство состоит из 7 независимо работающих элементов. Вероятность отказа каждого элемента за время Т равна 0,1. Найти вероятность отказа прибора, если для этого достаточно, чтобы отказали хотя бы три элемента из семи.
6) Телефонная станция обслуживает 200 абонентов. Для каждого абонента вероятность того, что в течении одного часа он позвонит на станции, равна 0,02. Найти вероятность того, что в течении часа позвонят: а) 5 абонентов; б) не менее трех абонентов.
7) Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка разобьется, равна 0,03. Найти вероятность того, что магазин получит разбитых бутылок: а) ровно две; б) более двух.
8) Среди семян пшеницы 0,6 % семян сорняков. Какова вероятность при случайном отборе 1000 семян обнаружить: а) ровно шесть семян сорняков; б) более трёх семян сорняков?
9) Игральную кость подбрасывают 180 раз. Найти вероятность того, что единица выпадет: а) 33 раза; б) от 20 до 29 раз; в) менее 35 раз; г) не менее 25 раз.
Тема 6. Дискретная случайная величина (ДСВ). Функция и характеристики распределения ДСВ
Задан закон распределения ДСВ X (см. ниже варианты заданий).
а) неизвестную вероятность р;
б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение s случайной величины;
в) функцию распределения F (x) и построить её график;
г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью y = f (x).
Варианты заданий по теме 6:
| xi | -2 | -1 | |||||
| pi | 0,01 | p | 0,23 | 0,28 | 0,19 | 0,11 | 0,06 |
| xi | -2 | -1 | |||||
| pi | 0,2 | 0,31 | 0,24 | p | 0,07 | 0,04 | 0,01 |
Математика без Ху%!ни. Теория вероятностей, комбинаторная вероятность.
y = 2 x + 3
| xi | -2 | -1 | |||||
| pi | 0,04 | 0,08 | 0,3 | 0,3 | 0,1 | 0,08 | p |
y = x 2 – 1
| xi | -2 | -1 | |||||
| pi | 0,42 | 0,23 | р | 0,10 | 0,06 | 0,03 | 0,01 |
y = –2 x + 1
| xi | -2 | -1 | |||||
| pi | р | 0,29 | 0,12 | 0,15 | 0,21 | 0,16 | 0,04 |
| xi | -2 | -1 | |||||
| pi | 0,05 | 0,12 | 0,18 | 0,30 | р | 0,12 | 0,05 |
y = 5 x – 2
| xi | -2 | -1 | |||||
| pi | 0,16 | 0,25 | 0,25 | 0,16 | 0,10 | р | 0,03 |
| xi | -2 | -1 | |||||
| pi | 0,06 | р | 0,12 | 0,2 | 0,3 | 0,1 | 0,03 |
y = x 2 + 2
| xi | -2 | -1 | |||||
| pi | 0,02 | 0,38 | 0,30 | р | 0,08 | 0,04 | 0,02 |
y = x 2 + 3
| xi | -2 | -1 | |||||
| pi | 0,08 | 0,1 | 0,14 | 0,1 | 0,1 | 0,1 | р |
Тема 7. Непрерывная случайная величина (НСВ). Функция распределения и плотность вероятности НСВ
НСВ Х имеет нормальное распределение с математическим ожиданием Mx и средним квадратичным отклонением σ x. Найти для заданных значений Mx, σ x, a, b (см. ниже таблицу вариантов):
1) вероятность попадания СВ Х в интервал (a; b): P (a < X < b);
3) сформулировать «правило трёх сигм»;
4) написать выражения для функции распределения F (x) и плотности вероятности f (x) и построить их графики;
5) на графиках указать полученные вероятности из пунктов 1 и 2;
6) найти квантиль x 0,7 и 20%-ю точку.
Варианты заданий по теме 7
| Вариант | Mx | σ x | a | b |
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Источник: cyberpedia.su
Классическое определение вероятности
Классической схемой, или схемой случаев, называется испытание, при котором число элементарных исходов конечно и все из них равновозможны.
Элементарное событие (исход) ω называется благоприятствующим событию А, если его появление влечет наступление событияА(т.е. ω входит в число элементов, составляющихА).
Классической вероятностьюсобытияАназывается отношение числаmэлементарных событий, благоприятствующих событиюА, к числуnвсех элементарных событий этой схемы
.
Из определения вероятности следует, что Р (Ø) = 0,
и
.
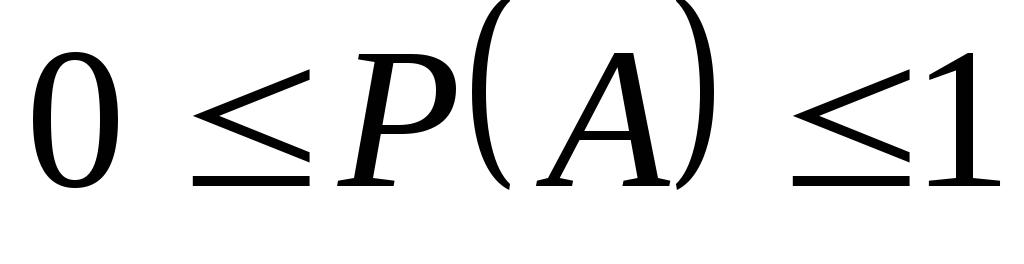Пример 2.7.В магазин поступило 40 новых цветных телевизоров, среди которых 7 имеют скрытые дефекты. Наудачу отбирается один телевизор для проверки. Какова вероятность, что он не имеет скрытых дефектов?
Решение. Число телевизоров, не имеющих скрытых дефектов, равно 
. Число всех элементарных исходов всех поступивших телевизоров равно
. Следовательно, по классическому определению вероятности вероятность того, что отобранный телевизор не имеет скрытых дефектов (событиеА), равна
.
Ответ:Р(А) = 0,825.
Пример 2.8.1 сентября на первом курсе одного из факультетов запланированы по расписанию три лекции из 10 различных предметов. Студент, не успевший ознакомиться с расписанием, пытается его угадать. Какова вероятность успеха в данном эксперименте, если считать, что любое расписание из трех предметов равновозможно.
Решение.Студенту необходимо из 10 лекций, которые могут быть поставлены в расписание, причем в определенном порядке, выбрать три. Следовательно, число всех возможных исходов испытания равно числу размещений из 10 по 3, т.е.
.
Благоприятный же случай только один, т.е. m = 1. Искомая вероятность будет равна
.
Ответ:.
Пример 2.9. В подъезде дома установили замок с кодом. Дверь автоматически отпирается, если в определенной последовательности набрать три цифры из возможных десяти. Некто вошел в подъезд и, не зная кода, стал наудачу пробовать различные комбинации из трех цифр. На каждую попытку он тратит 15 секунд. Какова вероятность события А = ?
Решение.Так как цифры, входящие в набираемый номер, могут повторяться и порядок их набора играет существенную роль, то мы приходим к схеме размещений с повторениями. Число возможных вариантов набора трех цифр из 10 возможных равно
За один час, тратя на набор комбинации 15 секунд, можно набрать 240 различных комбинаций, т.е.m = 240. Искомая вероятность
Ответ:
Пример 2.10.Найти вероятность того, что дни рождения 12 человек придутся на разные месяцы года.
Решение.Так как каждый из 12 человек может родиться в любом из 12 месяцев года, то число всех возможных вариантов можно посчитать по формуле размещений с повторениями
Число благоприятных случаев получим, переставляя месяцы рождения у этих 12 человек, т.е.
.
Тогда искомая вероятность будет равна
Ответ:
Пример 2.11.На полке стоят 15 книг, 5 из них в переплете. Берут наудачу три книги. Какова вероятность того, что все три книги в переплете?
Решение.Опыт состоит в том, что из 15 книг отбирают 3, причем в каком порядке они отобраны, роли не играет. Следовательно, число возможных способов выбора будет равно числу сочетаний из 15 по 3, т.е.
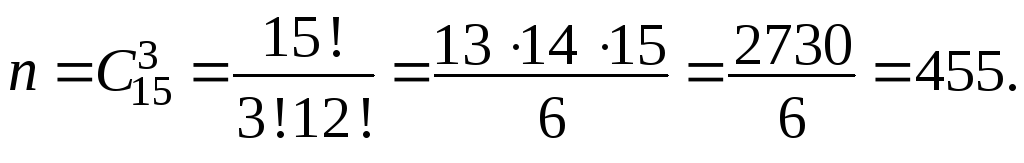
Число благоприятных случаев будет равно числу сочетаний из 5 по 3, т.е.
Искомая вероятность
Ответ:
Пример 2.12.В кондитерской имеются 6 видов пирожных. Очередной покупатель выбил чек на 3 пирожных. Считая, что любой заказываемый набор пирожных равновероятен, вычислить вероятность того, что покупатель заказал пирожные разных видов.
Решение.Число всех возможных видов заказов 3 пирожных будет равно числу сочетаний с повторениями из 6 элементов по 3, т.е.
Число благоприятных случаев будет равно числу сочетаний из 6 по 3, т.е.
Ответ:
Пример 2.13.Десять приезжих мужчин, среди которых Петров и Иванов, размещаются в гостинице в двух трехместных и одном четырехместном номерах. Какова вероятность событияА, состоящего в том, что Петров и Иванов попадут в четырехместный номер?
Решение.Число всех возможных размещений 10 человек в двух трехместных и одном четырехместном номере равно числу перестановок из десяти элементов, среди которых 3 одного вида, 3 другого и 4 третьего, т.е.
После того как Иванов и Петров будут размещены в четырехместном номере, остальные 8 человек должны быть размещены в двух трехместных и на оставшиеся два свободных места в четырехместном номере, это можно будет сделать следующим образом:
Искомая вероятность
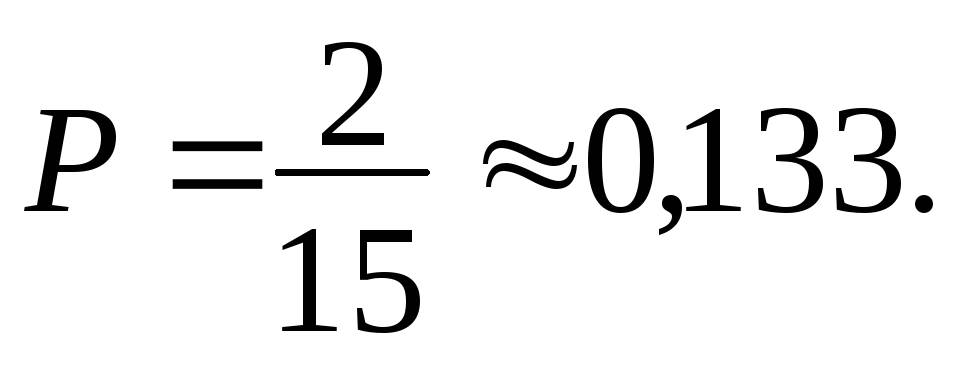
Ответ:
Источник: studfile.net
В магазин поступило 30 новых телевизоров, среди которых 5 имеют скрытые дефекты. Наудачу отбирается
В магазин поступило 30 новых телевизоров, среди которых 5 имеют скрытые дефекты. Наудачу отбирается один телевизор для проверки. Какова вероятность того, что он не имеет скрытых дефектов?
Число телевизоров, не имеющих скрытых дефектов, равно m=30-5=25. Число всех элементарных исходов всех поступивших телевизоров равно n=30. Следовательно, по классическому определению вероятности вероятность того, что отобранный телевизор не имеет скрытых дефектов (событие А),равна PA=mn=2530=0,833. Ответ: PA=0,833.
. Следовательно, по классическому определению вероятности вероятность того, что отобранный телевизор не имеет скрытых дефектов (событие А),равна
PA=mn=2530=0,833.
Ответ: PA=0,833.
Библиотека Ирины Эланс, основана как общедоступная библиотека в интернете. Онлайн-библиотеке академических ресурсов от Ирины Эланс доверяют студенты со всей России.
Библиотека Ирины Эланс
Полное или частичное копирование материалов разрешается только с указанием активной ссылки на сайт:
Ирина Эланс открыла библиотеку в 2007 году.
Источник: student-files.ru