Градиент на телевизоре что это такое

Нет аккаунта? Зарегистрироваться

Уроки, обзоры и размышления об продуктах Adobe, и не только

Что такое градиент и с чем его едят

• Jul. 20th, 2010 at 12:11 AM

В Adobe Photoshop, ровно как и в других графических программах подобного роба, вам часто придётся сталкиваться с таким понятием, как «Градиент». Давайте детально рассмотрим, что же это такое.
По сути, градиент — это плавный, постепенный переход от одного цвета к другому. Градиенты могут быть как двухцветными, так и многоцветными. В фотошопе есть специальный одноимённый инструмент — «Градиент», который расположен в одной ячейке с заливкой. Выбрав его, можно залить градиентом выделенную область, или абсолютно всё полотно, если таковая отсутствует.

Чтобы указать программе длительность и плавность градиента, нужно кликнуть в месте, где градиент будет начинаться, и не отпуская левой клавиши мыши, перетянуть линию-указатель в конец градиента. После того, как вы отпустите мышку, программа зальёт градиентом полотно так, как вы ей только что указали.

VRR для Sony. Свергнет ли это LG OLED со звания лучшего игрового телевизора? | ABOUT TECH

Градиенты по своей природе бывают :
— Линейные — те, в которые изменение цвета происходит как бы на одной линии;
— Радиальные — градиенты, которых есть центральная точка, и изменения цвета происходят по кругу от неё;
— Конические — когда в центре образовывается нечто, напоминающее вершину конуса, а по окружности её и происходят изменения цвета;
— Квадратные — когда в центре образовывается прикольная фигура в виде квадрата.
В Adobe Photoshop имеется несколько встроенных наборов градиентов, который всегда можно расширить, скачав и добавив туда сотни готовых образцов из интернета. Или всегда можно добавить свой градиент во встроенном редакторе градиентов. В нём можно выбирать и задавать цвета градиента, их количество, плавность перехода и многое другое.

Чтобы открыть этот редактор градиентов, нужно кликнуть левой клавише мыши на изображённой пиктограмме текущего градиента при выбранном инструменте «Градиент». В конце, создав устраивающее вас сочетание цветов, можно сохранить свой градиент в набор, и теперь он навсегда окажется в списке готовых образцов. Также можно экспортировать свой набор градиентов в отдельный файл, если вы хотите поделиться своим наборов градиентов со своими друзьями или коллегами.
P.S. Хотите узнать о том, что интересного происходит в недалёкой стране под названием Болгария? Читайте Новости Болгарии on-line каждый день! Надеюсь, вам будет интересно.

Источник: ffix1975.livejournal.com

Очки с градиентными линзами как способ защиты глаз от ультрафиолета

Телевизор Neo QLED | Как настроить игровой режим

Использование солнцезащитных очков в качестве повседневного аксессуара в летний период давно является популярным среди людей любых возрастов. Такие очки помогают не только защитить глаза от пагубно влияющих на их сетчатку солнечных лучей, но и предотвратить развитие многих офтальмологических заболеваний.

В этой статье

• Что такое градиентные линзы для очков?
• Виды градиентных линз в очках
• Плюсы и минусы градиента в очках
• Как выбрать градиентные солнцезащитные очки?

Именно поэтому подходить к выбору очков, защищающих зрение от солнечного излучения, следует с особой внимательностью и осторожностью, ведь в зависимости от того, какое они имеют покрытие или оттенок, определяется оказываемый ими эффект.

Что такое градиентные линзы для очков?

Впервые столкнувшись с проблемой подбора солнцезащитных очков, многие задаются вопросом: какими они бывают и каким стоит отдать предпочтение?

На сегодняшний день одними из самых распространенных солнцезащитных очков считаются градиентные очки.

Градиент в очках — это особенность их стекол, заключающаяся в неравномерном тонирующем напылении, цвет которого плавно переходит от темных оттенков к светлым. Более глубокие тона, заполняющие верхнюю часть линзы, ограничивают проникновение солнечного света, в то время как более светлые или прозрачные цвета позволяют детально рассматривать предметы даже при переменной облачности, в сумерках или в тени. Таким образом, градиентные линзы обеспечивают значительное снижение нагрузки на глаза и формируют равномерное распределение света.

Виды градиентных линз в очках

Существует множество вариаций градиентных линз. Наиболее часто их различают по 4 признакам:

1. По материалу изготовления — линзы могут быть стеклянными или пластиковыми.
2. По направлению линии осветления: выделяют классический тип и тип особого назначения. Первый представляет собой стекло, имеющее затемненный верх и осветленный низ. Вид особого назначения корректируется специалистом в сфере оптики, что выполняется на заказ — в таком случае осветляется середина линзы, а ее верхний и нижний края затемняются.
3. По наличию диоптрий — напыление наносят как на немедицинские солнцезащитные очки, так и на рекомендованные врачом.
4. По степени затемнения линз — линзы могут пропускать от 3% до 100% солнечного излучения.

Все эти факторы учитываются при выборе градиентных солнцезащитных очков, поскольку влияют на их последующее воздействие на глаза.

Плюсы и минусы градиента в очках

Градиентные очки имеют ряд весомых преимуществ перед другими солнцезащитными очками:

• Их не нужно снимать при смене освещенности — они позволяют видеть одинаково хорошо как в темном помещении, так и в ярко освещенном;
• Они снижают интенсивность ультрафиолетовых лучей;
• При их ношении четкость и палитра объектов не искажается;
• Градиентные линзы могут назначаться при патологиях зрения и имеют невысокую стоимость.

Помимо этого, внешний вид такого аксессуара во многом превосходит однотонные линзы для очков: градиент выглядит куда интереснее и контролирует напряжение и усталость глаз. Это делает его популярным не только среди молодежи, но и среди взрослого поколения.

Среди недостатков выделяют только непригодность градиента для слабовидящих людей: в данном случае градиентные линзы сильно ухудшают видимость и не рекомендуются к применению тем, кто страдает близорукостью.

Как выбрать градиентные солнцезащитные очки?

Подходя к выбору солнцезащитных очков, в первую очередь обращают внимание на материал, из которого были изготовлены линзы. Они могут быть сделаны из стекла или из пластика.

Стеклянные линзы имеют ряд не только положительных, но и отрицательных характеристик. К положительным относят:

• отсутствие искажения изображений;
• стойкую защиту от ультрафиолета;
• устойчивость к царапинам;
• простоту в чистке.

Однако минусов у стеклянных градиентных очков не меньше: они состоят из хрупкого и легко бьющегося стекла, склонны часто запотевать и полностью противопоказаны для детей.

Пластиковые линзы, напротив, отличаются большим списком позитивных показателей. Они:

• гарантируют защищенность от ультрафиолетовых лучей и абсолютное сохранение видимости;
• устойчивы к царапинам и ударам;
• имеют меньший вес, чем стеклянные, а потому более удобны;
• отличаются большей безопасностью и прочностью при падении.

И все же даже пластиковые очки не способны дать гарантию полной защищенности для глаз: нередко люди, покупая товары непроверенных производителей оптики, сталкиваются с некачественными изделиями, которые не только пропускают солнечное излучение, но и значительно искажают зрительное восприятие неправильной окраской или распределением цвета линз.

Следует помнить, что подобный предмет гардероба, имеющий значение для поддержания определенного уровня здоровья глаз, требует высокого качества.

В зависимости от того, с какой целью приобретаются очки и в каких ситуациях будут использоваться, рекомендуется применение определенных цветов:

• Для вождения: коричневый, медный, зеленый;
• Для отдыха и рыбалки: оттенки бурого, желтого и серого;
• Для общего расслабления глаз: зеленый.

Максимальную защиту для зрения обеспечивает коричневый цвет, в то время как зеленый считается наиболее подходящим для напряженной работы глаз (например, для поездок на автомобиле).

Вместе с этим обращают внимание на степень затемнения линз:

• Нулевая — очки могут пропускать от 80 до 100% солнечных лучей. Используются исключительно для коррекции зрения или в качестве стильной детали для создания имиджа.
• Первая — очки пропускают от 43 до 80% излучения. Такие очки подходят для ношения при облачной погоде.
• Вторая — от 18 до 43% света проникают сквозь линзы. Применяются в условиях умеренно солнечной погоды;
• Третья — самая комфортная и распространенная степень затемнения в очках — они пропускают от 8 до 18% лучей;
• Четвертая — использующаяся в условиях не только яркого солнечного света, но и наличия огромного количества отражающих поверхностей (в горах и на водных объектах). Строго воспрещены для водителей.

Категория затемнения линз указывается на внутренней стороне дужек очков единичной цифрой или с приставкой «cat.».

Иные показатели градиентных очков такие, как их форма или размер, определяются исключительно индивидуальными вкусовыми предпочтениями человека. Поэтому, задаваясь вопросом «что такое градиентные очки и как правильно их выбрать?», необходимо ориентироваться не только на общепринятые стандарты ношения солнцезащитных очков, но и на собственный вкус.

Размещено в Очки, 13.09.2019

Источник: www.ochkov.net

Градиентный спуск: всё, что нужно знать

Градиентный спуск — самый используемый алгоритм обучения нейронных сетей, он применяется почти в каждой модели машинного обучения. Метод градиентного спуска с некоторой модификацией широко используется для обучения персептрона и глубоких нейронных сетей, и известен как метод обратного распространения ошибки.

• Смысл ГС — объяснение всего алгоритма;
• Различные вариации алгоритма;
• Реализация кода: написание кода на языке Python.

Что такое градиентный спуск

Градиентный спуск — метод нахождения минимального значения функции потерь (существует множество видов этой функции). Минимизация любой функции означает поиск самой глубокой впадины в этой функции. Имейте в виду, что функция используется, чтобы контролировать ошибку в прогнозах модели машинного обучения. Поиск минимума означает получение наименьшей возможной ошибки или повышение точности модели. Мы увеличиваем точность, перебирая набор учебных данных при настройке параметров нашей модели (весов и смещений).

Итак, градиентный спуск нужен для минимизации функции потерь.

Суть алгоритма – процесс получения наименьшего значения ошибки. Аналогично это можно рассматривать как спуск во впадину в попытке найти золото на дне ущелья (самое низкое значение ошибки).

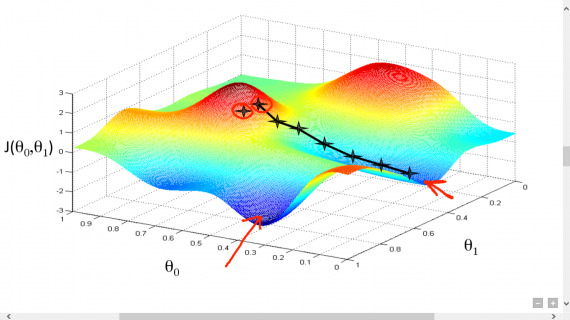
В дальнейшем, чтобы найти самую низкую ошибку (глубочайшую впадину) в функции потерь (по отношению к одному весу), нужно настроить параметры модели. Как мы их настраиваем? В этом поможет математический анализ. Благодаря анализу мы знаем, что наклон графика функции – производная от функции по переменной. Это наклон всегда указывает на ближайшую впадину!

На рисунке мы видим график функции потерь (названный «Ошибка» с символом «J») с одним весом. Теперь, если мы вычислим наклон (обозначим это dJ/dw) функции потерь относительно одного веса, то получим направление, в котором нужно двигаться, чтобы достичь локальных минимумов. Давайте пока представим, что наша модель имеет только один вес.

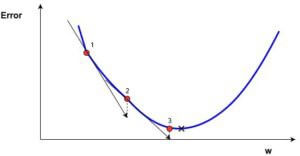
Функция потерь

Важно: когда мы перебираем все учебные данные, мы продолжаем добавлять значения dJ/dw для каждого веса. Так как потери зависят от примера обучения, dJ/dw также продолжает меняться. Затем делим собранные значения на количество примеров обучения для получения среднего. Потом мы используем это среднее значение (каждого веса) для настройки каждого веса.

Также обратите внимание: Функция потерь предназначена для отслеживания ошибки с каждым примером обучениям, в то время как производная функции относительного одного веса – это то, куда нужно сместить вес, чтобы минимизировать ее для этого примера обучения. Вы можете создавать модели даже без применения функции потерь. Но вам придется использовать производную относительно каждого веса (dJ/dw).

Теперь, когда мы определили направление, в котором нужно подтолкнуть вес, нам нужно понять, как это сделать. Тут мы используем коэффициент скорости обучения, его называют гипер-параметром. Гипер-параметр – значение, требуемое вашей моделью, о котором мы действительно имеем очень смутное представление. Обычно эти значения могут быть изучены методом проб и ошибок.

Здесь не так: одно подходит для всех гипер-параметров. Коэффициент скорости обучения можно рассматривать как «шаг в правильном направлении», где направление происходит от dJ/dw.

Это была функция потерь построенная на один вес. В реальной модели мы делаем всё перечисленное выше для всех весов, перебирая все примеры обучения. Даже в относительно небольшой модели машинного обучения у вас будет более чем 1 или 2 веса. Это затрудняет визуализацию, поскольку график будет обладать размерами, которые разум не может себе представить.

Подробнее о градиентах

Кроме функции потерь градиентный спуск также требует градиент, который является dJ/dw (производная функции потерь относительно одного веса, выполненная для всех весов). dJ/dw зависит от вашего выбора функции потерь. Наиболее распространена функция потерь среднеквадратичной ошибки.

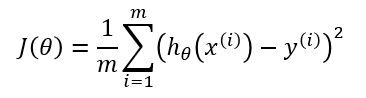
Производная этой функции относительно любого веса (эта формула показывает вычисление градиента для линейной регрессии):

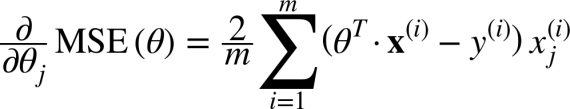
Это – вся математика в ГС. Глядя на это можно сказать, что по сути, ГС не содержит много математики. Единственная математика, которую он содержит в себе – умножение и деление, до которых мы доберемся. Это означает, что ваш выбор функции повлияет на вычисление градиента каждого веса.

Коэффициент скорости обучения

Всё, о чём написано выше, есть в учебнике. Вы можете открыть любую книгу о градиентном спуске, там будет написано то же самое. Формулы градиентов для каждой функции потерь можно найти в интернете, не зная как вывести их самостоятельно.

Однако проблема у большинства моделей возникает с коэффициентом скорости обучения. Давайте взглянем на обновленное выражение для каждого веса (j лежит в диапазоне от 0 до количества весов, а Theta-j это j-й вес в векторе весов, k лежит в диапазоне от 0 до количества смещений, где B-k — это k-е смещение в векторе смещений). Здесь alpha – коэффициент скорости обучения.

Из этого можно сказать, что мы вычисляем dJ/dTheta-j ( градиент веса Theta-j), и затем шаг размера alpha в этом направлении. Следовательно, мы спускаемся по градиенту. Чтобы обновить смещение, замените Theta-j на B-k.

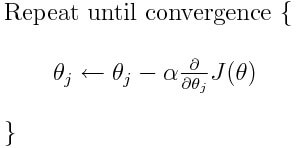
Если этот размера шага alpha слишком велик, мы преодолеем минимум: то есть промахнемся мимо минимума. Если alpha слишком мала, мы используем слишком много итераций, чтобы добраться до минимума. Итак, alpha должна быть подходящей.

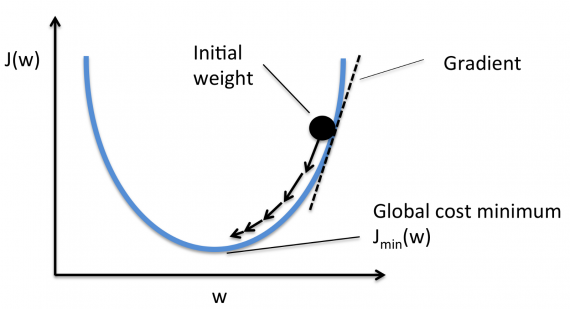
Использование градиентного спуска

Что ж, вот и всё. Это всё, что нужно знать про градиентный спуск. Давайте подытожим всё в псевдокоде.

Примечание: Весы здесь представлены в векторах. В более крупных моделях они, наверное, будут матрицами.

От i = 0 до «количество примеров обучения»

1. Вычислите градиент функции потерь для i-го примера обучения по каждому весу и смещению. Теперь у вас есть вектор, который полон градиентами для каждого веса и переменной, содержащей градиент смещения.

2. Добавьте градиенты весов, вычисленные для отдельного аккумулятивного вектора, который после того, как вы выполнили итерацию по каждому учебному примеру, должен содержать сумму градиентов каждого веса за несколько итераций.

3. Подобно ситуации с весами, добавьте градиент смещения к аккумулятивной переменной.

Теперь, ПОСЛЕ перебирания всех примеров обучения, выполните следующие действия:

1. Поделите аккумулятивные переменные весов и смещения на количество примеров обучения. Это даст нам средние градиенты для всех весов и средний градиент для смещения. Будем называть их обновленными аккумуляторами (ОА).

2. Затем, используя приведенную ниже формулу, обновите все веса и смещение. Вместо dJ / dTheta-j вы будете подставлять ОА (обновленный аккумулятор) для весов и ОА для смещения. Проделайте то же самое для смещения.

Это была только одна итерация градиентного спуска.

Повторите этот процесс от начала до конца для некоторого количества итераций. Это означает, что для 1-й итерации ГС вы перебираете все примеры обучения, вычисляете градиенты, потом обновляете веса и смещения. Затем вы проделываете это для некоторого количества итераций ГС.

Различные типы градиентного спуска

Существует 3 варианта градиентного спуска:

1. Мini-batch: тут, вместо поочерёдного перебора всех примеров обучения и произведения необходимых вычислений для каждого из них, мы производим вычисления для n примеров обучения сразу. Этот выбор подходит для очень больших наборов данных.

2. Стохастический градиентный спуск: в этом случае вместо перебора и использования всего набора примеров обучения мы применяем подход “используй только один”. Здесь нужно отметить несколько моментов:

• Набор примеров обучения необходимо перемешать перед каждым его проходом в ГС, чтобы перебирать их каждый раз в случайном порядке.
• Поскольку каждый раз используется только один пример обучения, то ваш путь к локальному минимуму будет очень неоптимальным;
• С каждой итерацией ГС вам нужно перемешать набор обучения и выбрать случайный пример обучения;
• Поскольку вы используете только один пример обучения, ваш путь к локальным минимумам будет очень шумным.

3. Серия ГС: это то, о чем написано в предыдущих разделах. Цикл на каждом примере обучения.

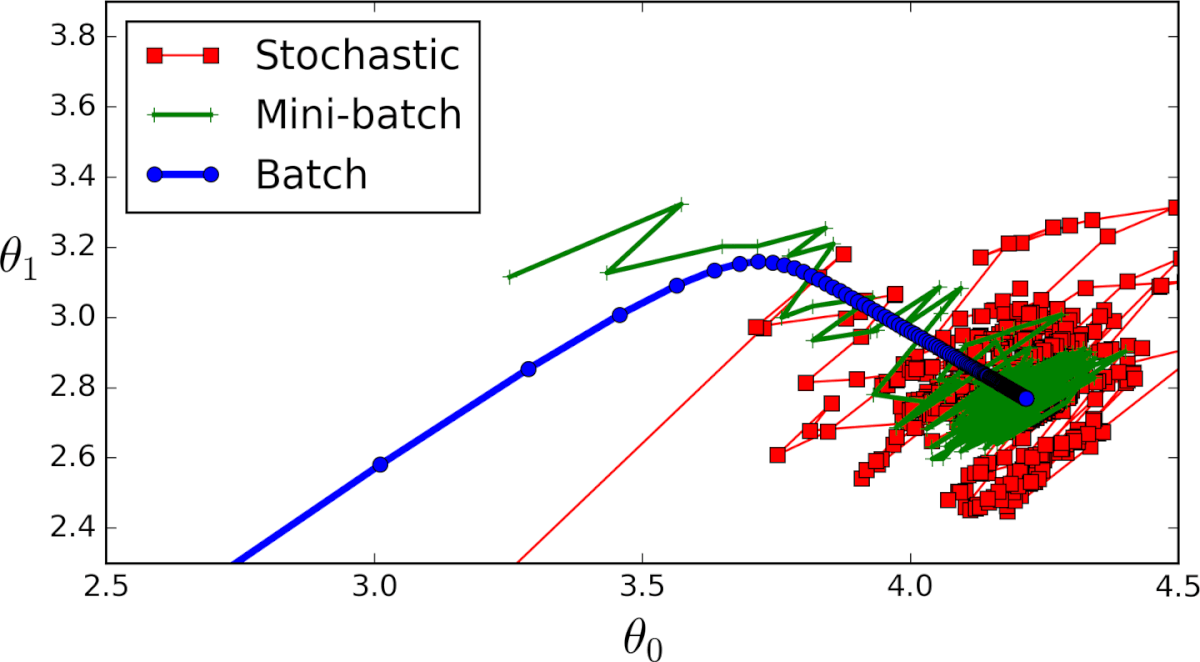
Пример кода на python

Применимо к cерии ГС, так будет выглядеть блок учебного кода на Python.

def train(X, y, W, B, alpha, max_iters): »’ Performs GD on all training examples, X: Training data set, y: Labels for training data, W: Weights vector, B: Bias variable, alpha: The learning rate, max_iters: Maximum GD iterations. »’ dW = 0 # Weights gradient accumulator dB = 0 # Bias gradient accumulator m = X.shape[0] # No. of training examples for i in range(max_iters): dW = 0 # Reseting the accumulators dB = 0 for j in range(m): # 1. Iterate over all examples, # 2. Compute gradients of the weights and biases in w_grad and b_grad, # 3. Update dW by adding w_grad and dB by adding b_grad, W = W — alpha * (dW / m) # Update the weights B = B — alpha * (dB / m) # Update the bias return W, B # Return the updated weights and bias.

Вот и всё. Теперь вы должны хорошо понимать, что такое метод градиентного спуска.

Источник: neurohive.io